苏科版九年级数学上册 第4章 等可能条件下的概率单元测试卷(word 版 含答案)
文档属性
| 名称 | 苏科版九年级数学上册 第4章 等可能条件下的概率单元测试卷(word 版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 367.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 15:59:57 | ||
图片预览



文档简介
第4章
等可能条件下的概率
一、选择题(共15小题;共60分)
1.
三张外观相同的卡片上分别标有数字
,,,从中随机一次抽出两张,这两张卡片上的数字之和恰好等于
的概率是
A.
B.
C.
D.
2.
小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是
A.
B.
C.
D.
3.
下列说法正确的是
A.
“本市明天降雨的可能性为
“说明明天有
时间在降雨
B.
“抛一枚硬币正面朝上的可能性为
”说明每抛硬币
次就有
次出现正面朝上
C.
”彩票中奖的可能性为
”表示买
张彩票一定有一张会中奖
D.
有
件物品放在
个抽屉里,至少有
个抽屉出现
件
4.
有编号为
到
的
个篮球,小红从中任意拿走一个,那么小红拿到的篮球的编号为
的整数倍的可能性的大小为
A.
B.
C.
D.
5.
布袋里装有
个白球和
个黑球,从中任意取出
个球,设事件
“取到的
个球都是白球”和事件
“取到的
个球都是黑球”发生的概率分别为
,,则
A.
B.
C.
D.
以上都有可能
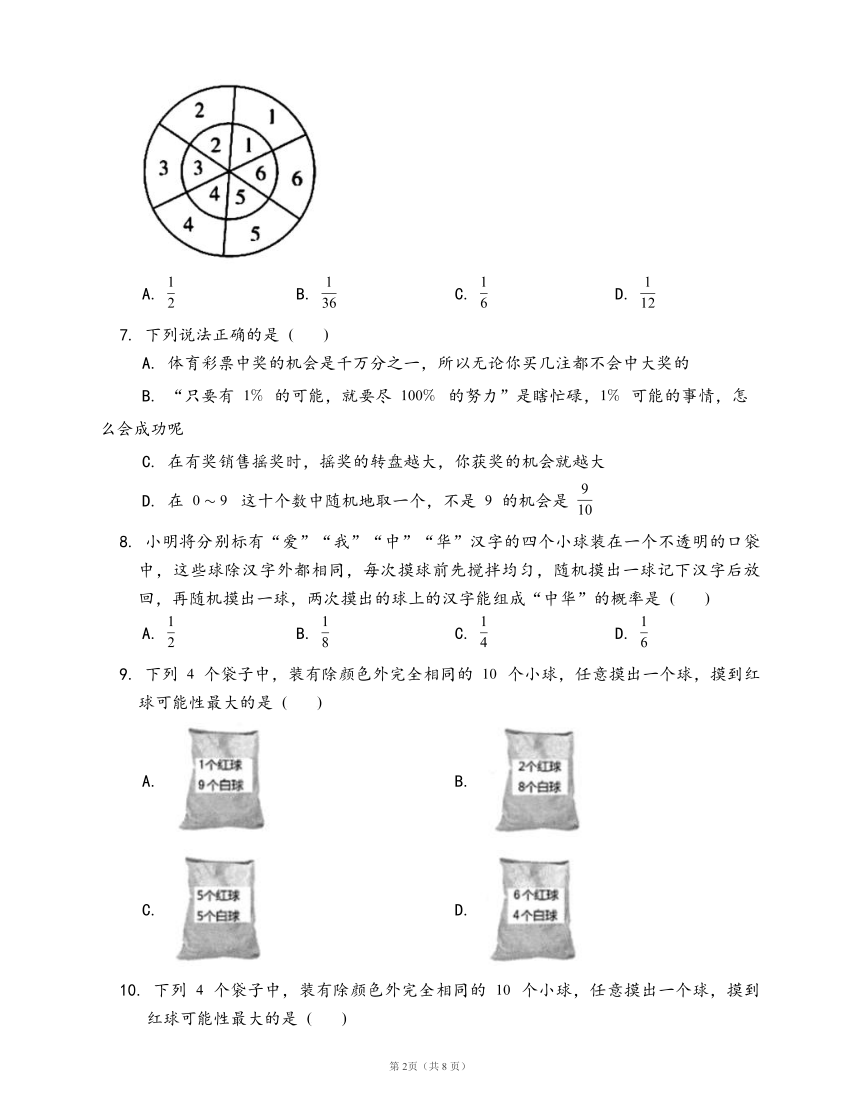
6.
如图,有两个同心转盘,现随意转动两转盘,两转盘静止后,恰出现如图情形(大转盘与小转盘的标号相对应)的概率为
A.
B.
C.
D.
7.
下列说法正确的是
A.
体育彩票中奖的机会是千万分之一,所以无论你买几注都不会中大奖的
B.
“只要有
的可能,就要尽
的努力”是瞎忙碌,
可能的事情,怎么会成功呢
C.
在有奖销售摇奖时,摇奖的转盘越大,你获奖的机会就越大
D.
在
这十个数中随机地取一个,不是
的机会是
8.
小明将分别标有“爱”“我”“中”“华”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外都相同,每次摸球前先搅拌均匀,随机摸出一球记下汉字后放回,再随机摸出一球,两次摸出的球上的汉字能组成“中华”的概率是
A.
B.
C.
D.
9.
下列
个袋子中,装有除颜色外完全相同的
个小球,任意摸出一个球,摸到红球可能性最大的是
A.
B.
C.
D.
10.
下列
个袋子中,装有除颜色外完全相同的
个小球,任意摸出一个球,摸到红球可能性最大的是
A.
B.
C.
D.
11.
四张完全相同的卡片上,分别画有圆、矩形、等边三角形、等腰梯形,现从中随机抽取一张,卡片上画的恰好是中心对称图形的概率为
A.
B.
C.
D.
12.
甲乙两同学各自掷一枚骰子(骰子上都有号码为
,,,,,),甲同学的号码比乙同学大的概率为
A.
B.
C.
D.
13.
一个质地均匀的正方体骰子任意掷两次,下列说法正确的是
A.
得到的数字和必然是偶数
B.
得到的数字和可能是奇数
C.
得到的数字和不可能是
D.
得到的数字和可能是
14.
有四张质地相同的卡片,它们的背面相同,其中两张的正面印有“粽子”的图案,另外两张的正面印有“龙舟”的图案,现将它们背面朝上,洗均匀后排列在桌面,任意翻开两张,那么两张图案一样的概率是
A.
B.
C.
D.
15.
要在一只口袋中装入若干个形状与大小都完全相同的球,使得从袋中摸到红球的概率为
,四位同学分别采用了下列装法,你认为他们中装错的是
A.
口袋中装入
个小球,其中只有两个红球
B.
装入
个红球,
个白球,
个黄球,
个蓝球,
个黑球
C.
装入红球
个,白球
个,黑球
个
D.
装入红球
个,白球
个,黑球
个,黄球
个
二、填空题(共8小题;共40分)
16.
从两副拿掉大、小王的扑克牌中,各抽取
张,
张牌都是红桃的概率是
?.
17.
某班要选
名同学代表参加班级间的交流活动.现在按下面的办法选取:把全班同学的姓名分别写在没有明显差别的纸片上,把纸片混放在一个盒子里,充分搅拌后,随机抽取
张,按照纸片上所写的名字选取
名同学.你觉得上面的选取过程是简单随机抽样吗?
?(填“是”或“不是”).
18.
用
万元资金投资一项技术改造项目,如果成功,则可盈利
万元;如果失败,将亏损全部投资.已知成功的概率是
,这次投资项目期望大致可盈利
?
万元.
19.
从学校任选一位同学,事件
:该同学是八年级的,事件
:该同学是九年级()班的,事件
:该同学是男的,用
,,
分别表示事件
,,
发生的可能性大小,按从小到大的顺序排列是
?.
20.
袋中共有
个大小相同的红球、白球,任意摸出一球是红球的概率为
,任意摸出
个球均为红球的概率是
?.
21.
现有下列长度的五根木棒:,,,,,从中任取三根,可以组成三角形的概率为
?.
22.
现有四张正面分别标有数字
,,,
的不透明卡片,它们除数字外其余完全相同,将它们背而面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为
,,则点
在第二象限的概率为
?.
23.
掷两枚骰子,出现点数之和为
的概率是
?.
三、解答题(共4小题;共50分)
24.
某班级准备召开主题班会,现从由
名男生和
名女生所组成的班委中,随机选取产生主持人.
(1)若选取一人担任主持人,则恰好是女生担任主持人的概率为
?;
(2)若选取两人担任主持人,求两名主持人恰好为一男一女的概率.(请用画树状图或列表等方法写出求解过程)
25.
有人说如果随机事件
的概率
,那么由
,可知在相同的条件下重复
次,事件
肯定发生,你认为他的说法对吗?
26.
掷两枚骰子.求:
(1)点数相同的可能性的大小.
(2)点数和为
的可能性的大小.
(3)点数和为
的可能性的大小.
(4)点数和大于
的可能性的大小.
27.
甲乙两人玩骰子,他们各自掷一枚骰子,对掷出的两个数进行某种运算,根据运算的结果来定胜负.但进行什么样的运算才公平,两人争论不休.后来他们提出了下面两个方案:
①两数之和等于
时甲胜,两数之和等于
时乙胜;
②两数之和大于
时甲胜,两数差的绝对值小于
时乙胜.
请你用列表法分析这两个方案.这样的方案公平吗?如果不公平,试修改相应的规则,使游戏变得公平.
答案
第一部分
1.
B
2.
B
3.
D
4.
B
5.
B
6.
C
7.
D
8.
B
【解析】列表得:
因为
种可能的结果中,能组成“中华”有
种可能,共
种,
所以两次摸出的球上的汉字能组成“中华”的概率
.
9.
D
10.
D
11.
B
12.
B
13.
B
14.
A
【解析】根据题意,画出树形图.
由图可知,任意翻开两张,共有
种等可能情况,其中两张图案一样的共有
种情况,
故任意翻开两张,其中两张图案一样的概率为
.
15.
C
【解析】A、摸到红球的概率为
;
B、摸到红球的概率为
;
C、摸到红球的概率为
;
D、摸到红球的概率为
.
故选C.
第二部分
16.
17.
是
18.
【解析】(万元)
19.
20.
【解析】题意可得红球有
个,白球有
个.列出所有等可能情况,如下表.由表可知,任意摸出两个球共有
种情况,其中摸到的
个球均为红球的有
种,所以任意摸出
个球均为红球的概率为
.
21.
【解析】,,,,,从中任取三根,
所有情况为:,,;,,;,,;,,;,,;,,;,,;,,;,,;,,;
共有
种等可能的结果数,其中可以组成三角形的结果数为
,
可以组成三角形的概率
.
22.
23.
第三部分
24.
(1)
??????(2)
画出树形图为:
共有
种等可能的结果数,其中恰好为一男一女的结果数为
,
所以
(主持人恰好为一男一女).
25.
不对.在相同条件下重复
次的试验中,事件
发生的概率是
而非
.
26.
(1)
.
??????(2)
.
??????(3)
.
??????(4)
.
27.
掷两枚骰子共有
个等可能结果,“两数和为
”有
种结果,“两数和为
”有
种结果;“两数和大于
”有
种结果,“两数差的绝对值小于
”有
,,,,,,,,,,,,,,,,共
种结果,故方案①②都不公平.公平游戏规则有很多,如“两数之和等于
时甲胜,两数之和等于
则乙胜”;“两数差等于
时甲胜,两数差的绝对值等于
则乙胜”.
第5页(共8
页)
等可能条件下的概率
一、选择题(共15小题;共60分)
1.
三张外观相同的卡片上分别标有数字
,,,从中随机一次抽出两张,这两张卡片上的数字之和恰好等于
的概率是
A.
B.
C.
D.
2.
小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是
A.
B.
C.
D.
3.
下列说法正确的是
A.
“本市明天降雨的可能性为
“说明明天有
时间在降雨
B.
“抛一枚硬币正面朝上的可能性为
”说明每抛硬币
次就有
次出现正面朝上
C.
”彩票中奖的可能性为
”表示买
张彩票一定有一张会中奖
D.
有
件物品放在
个抽屉里,至少有
个抽屉出现
件
4.
有编号为
到
的
个篮球,小红从中任意拿走一个,那么小红拿到的篮球的编号为
的整数倍的可能性的大小为
A.
B.
C.
D.
5.
布袋里装有
个白球和
个黑球,从中任意取出
个球,设事件
“取到的
个球都是白球”和事件
“取到的
个球都是黑球”发生的概率分别为
,,则
A.
B.
C.
D.
以上都有可能
6.
如图,有两个同心转盘,现随意转动两转盘,两转盘静止后,恰出现如图情形(大转盘与小转盘的标号相对应)的概率为
A.
B.
C.
D.
7.
下列说法正确的是
A.
体育彩票中奖的机会是千万分之一,所以无论你买几注都不会中大奖的
B.
“只要有
的可能,就要尽
的努力”是瞎忙碌,
可能的事情,怎么会成功呢
C.
在有奖销售摇奖时,摇奖的转盘越大,你获奖的机会就越大
D.
在
这十个数中随机地取一个,不是
的机会是
8.
小明将分别标有“爱”“我”“中”“华”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外都相同,每次摸球前先搅拌均匀,随机摸出一球记下汉字后放回,再随机摸出一球,两次摸出的球上的汉字能组成“中华”的概率是
A.
B.
C.
D.
9.
下列
个袋子中,装有除颜色外完全相同的
个小球,任意摸出一个球,摸到红球可能性最大的是
A.
B.
C.
D.
10.
下列
个袋子中,装有除颜色外完全相同的
个小球,任意摸出一个球,摸到红球可能性最大的是
A.
B.
C.
D.
11.
四张完全相同的卡片上,分别画有圆、矩形、等边三角形、等腰梯形,现从中随机抽取一张,卡片上画的恰好是中心对称图形的概率为
A.
B.
C.
D.
12.
甲乙两同学各自掷一枚骰子(骰子上都有号码为
,,,,,),甲同学的号码比乙同学大的概率为
A.
B.
C.
D.
13.
一个质地均匀的正方体骰子任意掷两次,下列说法正确的是
A.
得到的数字和必然是偶数
B.
得到的数字和可能是奇数
C.
得到的数字和不可能是
D.
得到的数字和可能是
14.
有四张质地相同的卡片,它们的背面相同,其中两张的正面印有“粽子”的图案,另外两张的正面印有“龙舟”的图案,现将它们背面朝上,洗均匀后排列在桌面,任意翻开两张,那么两张图案一样的概率是
A.
B.
C.
D.
15.
要在一只口袋中装入若干个形状与大小都完全相同的球,使得从袋中摸到红球的概率为
,四位同学分别采用了下列装法,你认为他们中装错的是
A.
口袋中装入
个小球,其中只有两个红球
B.
装入
个红球,
个白球,
个黄球,
个蓝球,
个黑球
C.
装入红球
个,白球
个,黑球
个
D.
装入红球
个,白球
个,黑球
个,黄球
个
二、填空题(共8小题;共40分)
16.
从两副拿掉大、小王的扑克牌中,各抽取
张,
张牌都是红桃的概率是
?.
17.
某班要选
名同学代表参加班级间的交流活动.现在按下面的办法选取:把全班同学的姓名分别写在没有明显差别的纸片上,把纸片混放在一个盒子里,充分搅拌后,随机抽取
张,按照纸片上所写的名字选取
名同学.你觉得上面的选取过程是简单随机抽样吗?
?(填“是”或“不是”).
18.
用
万元资金投资一项技术改造项目,如果成功,则可盈利
万元;如果失败,将亏损全部投资.已知成功的概率是
,这次投资项目期望大致可盈利
?
万元.
19.
从学校任选一位同学,事件
:该同学是八年级的,事件
:该同学是九年级()班的,事件
:该同学是男的,用
,,
分别表示事件
,,
发生的可能性大小,按从小到大的顺序排列是
?.
20.
袋中共有
个大小相同的红球、白球,任意摸出一球是红球的概率为
,任意摸出
个球均为红球的概率是
?.
21.
现有下列长度的五根木棒:,,,,,从中任取三根,可以组成三角形的概率为
?.
22.
现有四张正面分别标有数字
,,,
的不透明卡片,它们除数字外其余完全相同,将它们背而面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为
,,则点
在第二象限的概率为
?.
23.
掷两枚骰子,出现点数之和为
的概率是
?.
三、解答题(共4小题;共50分)
24.
某班级准备召开主题班会,现从由
名男生和
名女生所组成的班委中,随机选取产生主持人.
(1)若选取一人担任主持人,则恰好是女生担任主持人的概率为
?;
(2)若选取两人担任主持人,求两名主持人恰好为一男一女的概率.(请用画树状图或列表等方法写出求解过程)
25.
有人说如果随机事件
的概率
,那么由
,可知在相同的条件下重复
次,事件
肯定发生,你认为他的说法对吗?
26.
掷两枚骰子.求:
(1)点数相同的可能性的大小.
(2)点数和为
的可能性的大小.
(3)点数和为
的可能性的大小.
(4)点数和大于
的可能性的大小.
27.
甲乙两人玩骰子,他们各自掷一枚骰子,对掷出的两个数进行某种运算,根据运算的结果来定胜负.但进行什么样的运算才公平,两人争论不休.后来他们提出了下面两个方案:
①两数之和等于
时甲胜,两数之和等于
时乙胜;
②两数之和大于
时甲胜,两数差的绝对值小于
时乙胜.
请你用列表法分析这两个方案.这样的方案公平吗?如果不公平,试修改相应的规则,使游戏变得公平.
答案
第一部分
1.
B
2.
B
3.
D
4.
B
5.
B
6.
C
7.
D
8.
B
【解析】列表得:
因为
种可能的结果中,能组成“中华”有
种可能,共
种,
所以两次摸出的球上的汉字能组成“中华”的概率
.
9.
D
10.
D
11.
B
12.
B
13.
B
14.
A
【解析】根据题意,画出树形图.
由图可知,任意翻开两张,共有
种等可能情况,其中两张图案一样的共有
种情况,
故任意翻开两张,其中两张图案一样的概率为
.
15.
C
【解析】A、摸到红球的概率为
;
B、摸到红球的概率为
;
C、摸到红球的概率为
;
D、摸到红球的概率为
.
故选C.
第二部分
16.
17.
是
18.
【解析】(万元)
19.
20.
【解析】题意可得红球有
个,白球有
个.列出所有等可能情况,如下表.由表可知,任意摸出两个球共有
种情况,其中摸到的
个球均为红球的有
种,所以任意摸出
个球均为红球的概率为
.
21.
【解析】,,,,,从中任取三根,
所有情况为:,,;,,;,,;,,;,,;,,;,,;,,;,,;,,;
共有
种等可能的结果数,其中可以组成三角形的结果数为
,
可以组成三角形的概率
.
22.
23.
第三部分
24.
(1)
??????(2)
画出树形图为:
共有
种等可能的结果数,其中恰好为一男一女的结果数为
,
所以
(主持人恰好为一男一女).
25.
不对.在相同条件下重复
次的试验中,事件
发生的概率是
而非
.
26.
(1)
.
??????(2)
.
??????(3)
.
??????(4)
.
27.
掷两枚骰子共有
个等可能结果,“两数和为
”有
种结果,“两数和为
”有
种结果;“两数和大于
”有
种结果,“两数差的绝对值小于
”有
,,,,,,,,,,,,,,,,共
种结果,故方案①②都不公平.公平游戏规则有很多,如“两数之和等于
时甲胜,两数之和等于
则乙胜”;“两数差等于
时甲胜,两数差的绝对值等于
则乙胜”.
第5页(共8
页)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
