矩形的判定

(共15张PPT)
初中数学九年级下册
（苏科版）
矩形的判定
一、知识回顾：
1、矩形的性质有哪些？
2、矩形的定义如何描述？
3、判定一个图形是矩形还有哪些方法？
1.有一个角是直角的平行四边形是矩形。
2. 对角线相等的平行四边形是矩形。
3、有三个角是直角的四边形是矩形。
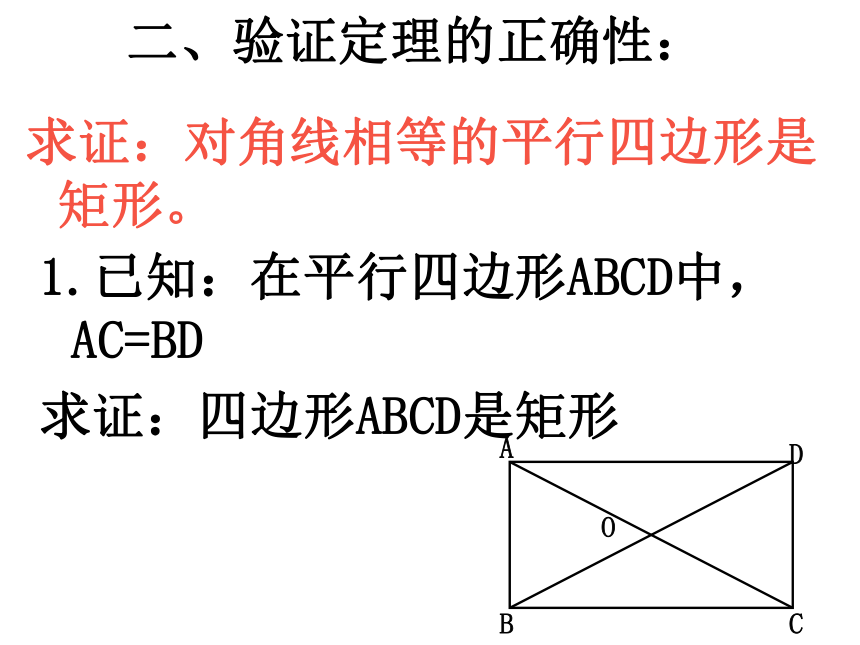
1.已知：在平行四边形ABCD中， AC=BD
求证：四边形ABCD是矩形
B
A
C
D
O
求证：对角线相等的平行四边形是矩形。
二、验证定理的正确性：
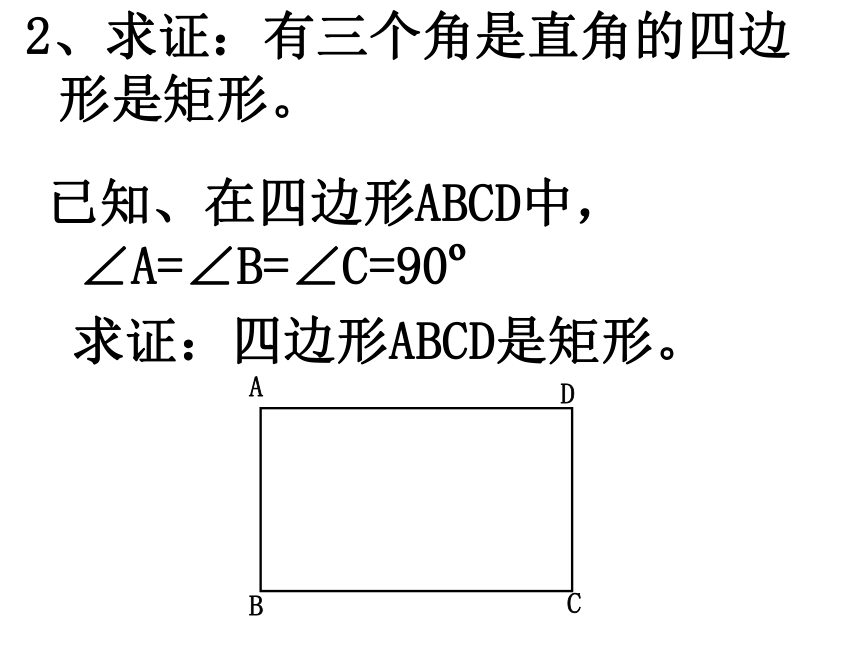
已知、在四边形ABCD中， ∠A=∠B=∠C=90
求证：四边形ABCD是矩形。
A
B
C
D
2、求证：有三个角是直角的四边形是矩形。
三、牛刀小试
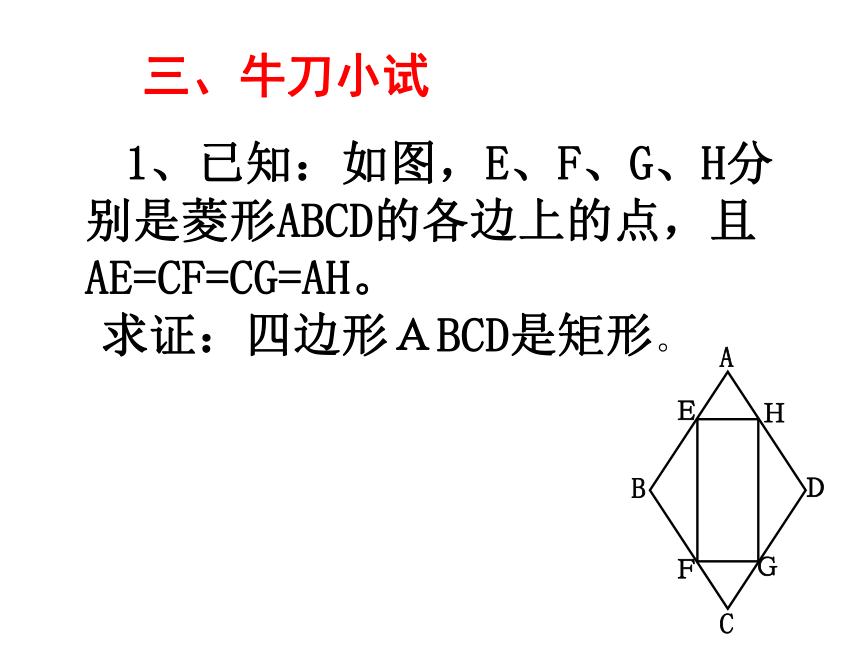
1、已知：如图，E、F、G、H分别是菱形ABCD的各边上的点，且AE=CF=CG=AH。
求证：四边形ＡBCD是矩形。
A
B
C
Ｄ
Ｅ
Ｆ
Ｇ
Ｈ
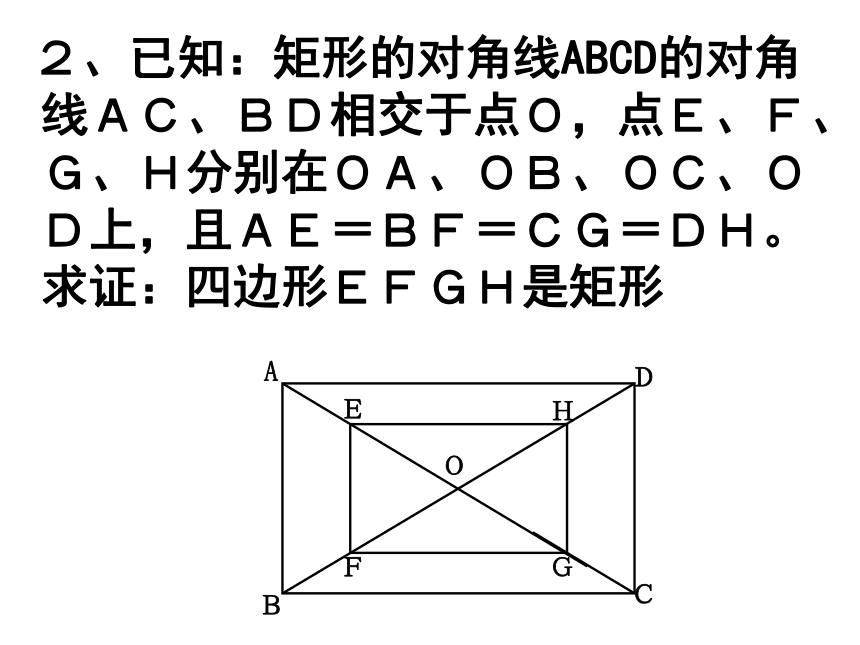
２、已知：矩形的对角线ABCD的对角线ＡＣ、ＢＤ相交于点Ｏ，点Ｅ、Ｆ、Ｇ、Ｈ分别在ＯＡ、ＯＢ、ＯＣ、ＯＤ上，且ＡＥ＝ＢＦ＝ＣＧ＝ＤＨ。求证：四边形ＥＦＧＨ是矩形
Ｂ
A
Ｃ
Ｄ
Ｏ
Ｅ
Ｆ
Ｇ
Ｈ
四、挑战自我
１.已知：平行四边形的对角线相交于点Ｏ。分别添加下列条件：
(1)∠ABC＝90 (2)AC⊥BD (3)AB=BC
(4)AC平分∠BAD(5)AO=DO
　使得四边形ABCD为矩形的条件的序号为
B
A
C
D
O
2.已知：平行四边形ABCD的四个内角的平分线分别相交于E、F、G、H。　　　　　　　　　　
　试证明：四边形EFGH为矩形
反例：
如等腰梯形
思考：
对角线相等的四边形是矩形吗？
在△ABC中，点D在AB上，且AD=CD=BD，DE、DF分别是∠BDC、 ∠ADC的平分线。四边形FDEC是矩形吗？为什么？
判断题：
1、内角都相等的四边形是矩形。（ ）
2、对角线相等的四边形是矩形。 （ ）
3、对角线相等的平行四边形是矩形。 （ ）
4、对角线互相平分且相等的四边形是矩形（ ）
5、邻角相等的平行四边形是矩形。 （ ）
6、对角互补的平行四边形是矩形。 （ ）
7、 ABCD中，AB=6，BC=8，AC=10， 则四边形ABCD是矩形 。 （ ）
√
╳
√
√
√
√
√
例1、BD、BE分别是∠ABC与它的邻补角的平分线，AE⊥BE，AD⊥BD，求证：四边形AEBD是矩形。
A
B
C
D
E
P
1
2
例题3：已知: ABCD的对角线AC、BD相交于点O， △ AOB是等边三角形，AB=4㎝，求这个平行四边形的面积。
五、总结提升
１、矩形的判定定理
（1）对角线相等的平行四边形是矩形。
（2）有三个角是直角的四边形是矩形。
２、矩形的性质在证明中的应用。
（对角线相等和四个角都是直角）
３、线段和角转移的方法。