菱形的判定

(共25张PPT)
1.3.7 菱形的判定
教学目标：
1.会证明菱形的判定定理。
2.能运用菱形的判定定理进行计算与证明。
教学重点：
菱形判定定理的应用。
教学难点：
菱形判定定理的证明。
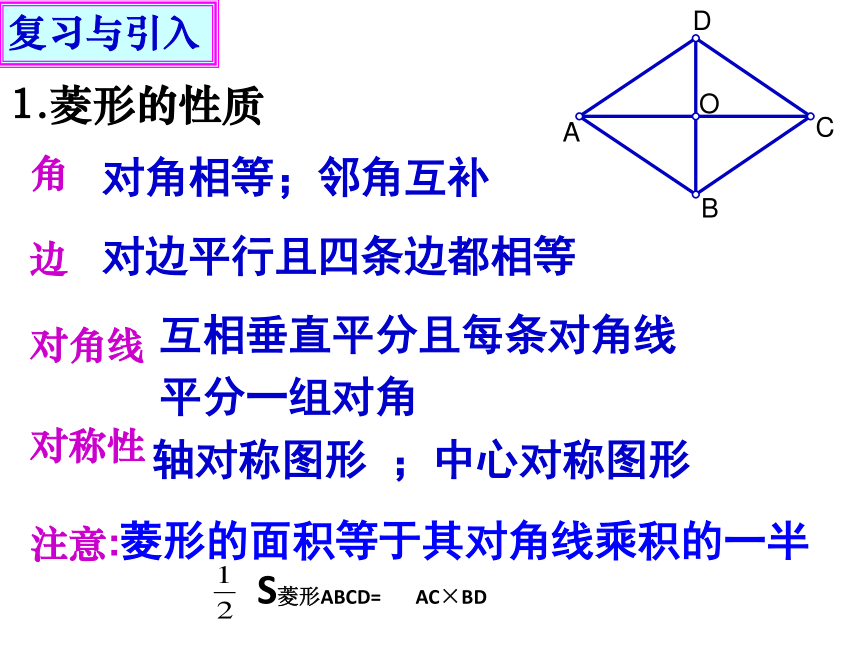
1.菱形的性质
复习与引入
角
对角相等；邻角互补
边
对边平行且四条边都相等
对角线
互相垂直平分且每条对角线
平分一组对角
对称性
轴对称图形 ；中心对称图形
注意:菱形的面积等于其对角线乘积的一半
S菱形ABCD= AC×BD
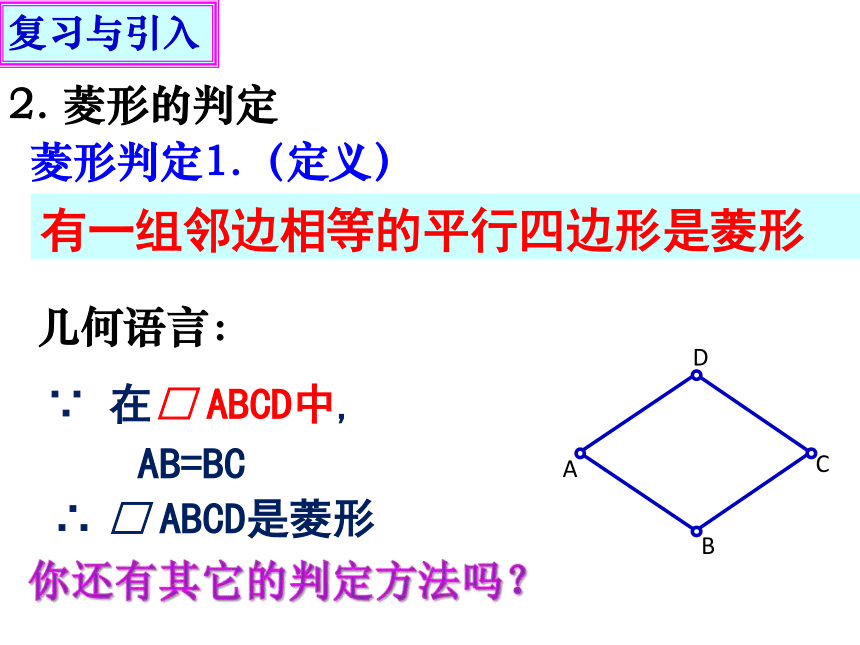
菱形判定1.（定义）
有一组邻边相等的平行四边形是菱形
∵ 在□ ABCD中,
AB=BC
∴ □ ABCD是菱形
几何语言：
A
C
D
B
2. 菱形的判定
复习与引入
2、菱形的判定
(1)一组邻边相等的平行四边形是菱形(定义).
(2)四条边都相等的四边形是菱形；
(3)对角线互相垂直的平行四边形是菱形,
使用判定定理是要注意基础图形是
四边形还是平行四边形
复习与引入
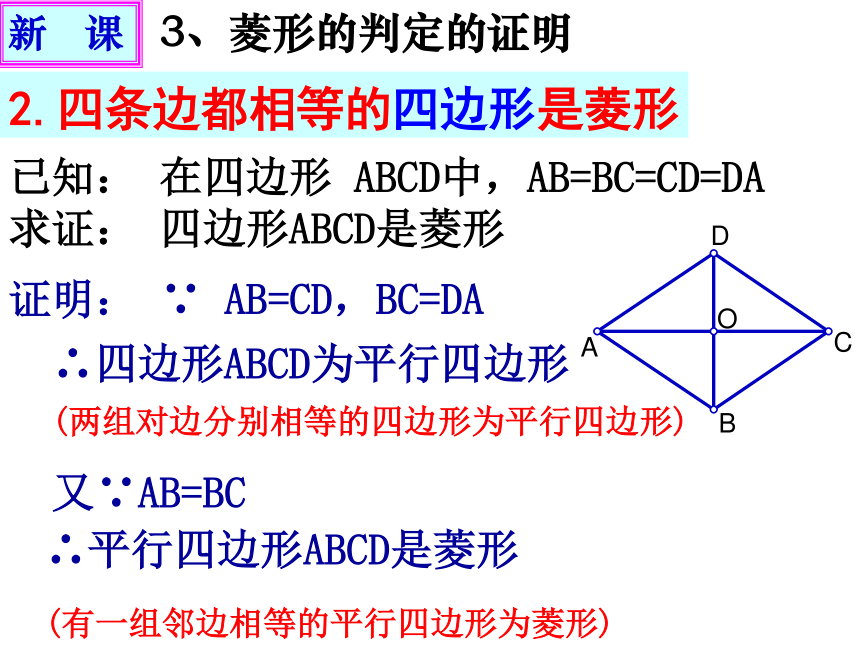
2.四条边都相等的四边形是菱形
证明： ∵ AB=CD，BC=DA
∴四边形ABCD为平行四边形
又∵AB=BC
∴平行四边形ABCD是菱形
已知： 在四边形 ABCD中，AB=BC=CD=DA 求证： 四边形ABCD是菱形
(两组对边分别相等的四边形为平行四边形)
(有一组邻边相等的平行四边形为菱形)
新 课
3、菱形的判定的证明
∴ □ ABCD是菱形. （一组邻边相等的平行四边形是菱形）
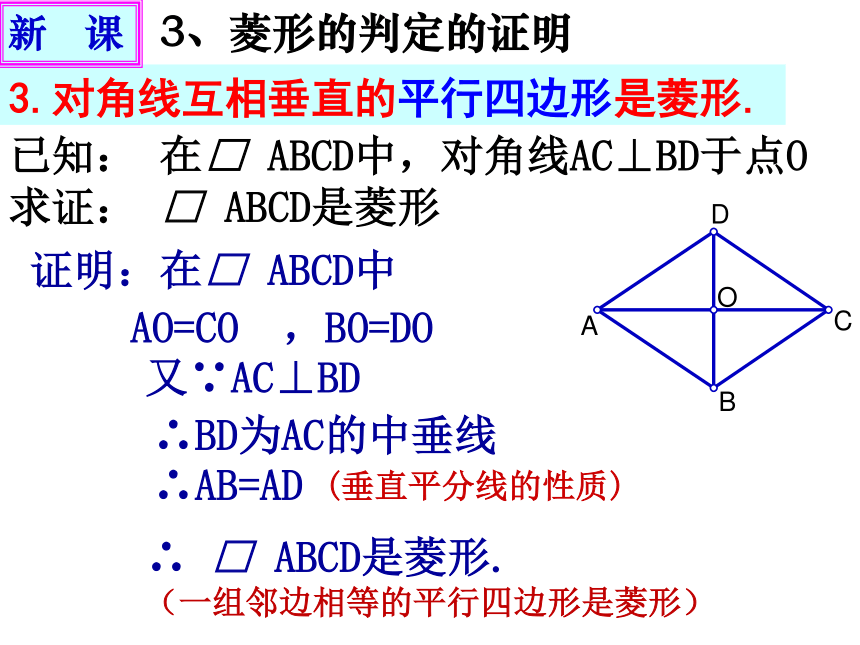
3.对角线互相垂直的平行四边形是菱形.
证明：在□ ABCD中
又∵AC⊥BD
∴BD为AC的中垂线
∴AB=AD
AO=CO ，BO=DO
已知： 在□ ABCD中，对角线AC⊥BD于点O 求证： □ ABCD是菱形
(垂直平分线的性质)
新 课
3、菱形的判定的证明
你能用直尺和圆规作一个菱形吗？请作图并说明理由。
思考与探索
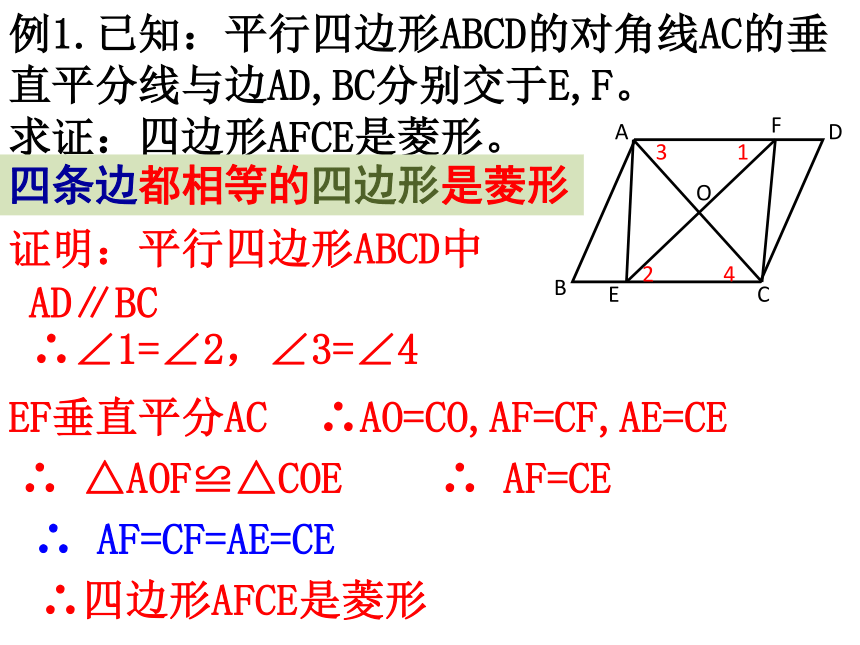
例1.已知：平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证：四边形AFCE是菱形。
A
B
E
D
C
F
O
1
2
证明：平行四边形ABCD中
AD∥BC
∴∠1=∠2，∠3=∠4
4
3
EF垂直平分AC
∴AO=CO,AF=CF,AE=CE
∴ △AOF≌△COE
∴ AF=CE
∴ AF=CF=AE=CE
∴四边形AFCE是菱形
四条边都相等的四边形是菱形
例1.已知：平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证：四边形AFCE是菱形。
A
B
E
D
C
F
O
1
2
证明：平行四边形ABCD中
AD∥BC
∴∠1=∠2，∠3=∠4
4
3
EF垂直平分AC
∴AO=CO,AF=CF,
∴ △AOF≌△COE
∴ AF=CE
∴平行四边形四边形AFCE是菱形
又AF∥CE
∴四边形AFCE是平行四边形
一组邻边相等的平行四边形是菱形
例1.已知：平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证：四边形AFCE是菱形。
A
B
E
D
C
F
O
1
2
3’证明：平行四边形ABCD中
AD∥BC
∴∠1=∠2，∠3=∠4
4
3
EF垂直平分AC
∴AO=CO,AC⊥EF,
∴ △AOF≌△COE
∴ AF=CE
∴平行四边形四边形AFCE是菱形
又AF∥CE
∴四边形AFCE是平行四边形
对角线互相垂直的平行四边形是菱形
邻边相等
对角线互相垂直
平行四边形
A
D
B
C
平行四边形
A
B
C
D
AD=DC
AC⊥BD
四边相等
四边形
A
B
C
D
AD=DC=CB=BA
对角线互相垂直平分
四边形
A
B
C
D
AC⊥BD,AO=CO,BO=DO
O
归 纳
例2.如图，△ABC中，AB=AC，D为BC的中点，DE⊥AB于E,DF⊥AC于F, EH⊥AC于H, FG⊥AB于G.GF,EH相交于P. 求证：四边形PEDF是菱形。
A
B
E
D
C
G
H
F
P
证明：连接AD
∵△ABC中，AB=AC, D为BC的中点
∴AD平分∠BAC
∵DE⊥AB ,DF⊥AC
∴DE=DF
∵ DE⊥AB , FG⊥AB
∴DE∥FG
同理可证∴DF∥EH
∴四边形PEDF是平行四边形
∴四边形PEDF是菱形。
∴∠DEG=∠FGA=90°
例3.如图，已知AD是△ABC的角平分线，
DE∥AC交AB于E，DF∥AB交AC于F，
求证：AD⊥EF。
1
2
3
A
B
C
E
D
F
证明：∵DE∥AC ,DF∥AB
∴四边形AEDF是平行四边形
∴ ∠2=∠3
∵ AD是△ABC的角平分线
∴ ∠1=∠2
∴ ∠1=∠3
∴ AE=DE
∴ □AEDF是菱形
∴ AD⊥EF
∵DE∥AC
（4）有一组邻边相等的四边形是菱形；
1、判断下列命题是否正确，并说明理由：
（1）对角线互相平分且邻边相等的四边
形是菱形；
（2）两组对边分别平行且一组邻边相等
的四边形是菱形；
（3）邻角相等的四边形是菱形；
练 习
X
X
（8）一条对角线平分一个内角的平行四边形是菱形。
（5）两组对角分别相等且对角线互相垂直的四边形是菱形；
（6）对角线互相垂直的四边形是菱形；
（7）对角线互相垂直平分的四边形是菱形；
练 习
X
2.下列条件中,不能判定四边形ＡＢＣＤ为菱形的是（　　）．
Ａ、AC⊥BD ，AC与BD互相平分
Ｂ、AB=BC=CD=DA
Ｃ、AB=BC，AD=CD，且AC ⊥BD
Ｄ、AB=CD，AD=BC，AC ⊥BD
O
A
D
C
B
练 习
C
3、已知：如图，矩形ABCD的对角线AC、BD相交于点O，AP∥BD，DP∥AC，AP、DP相交于点P。求证：四边形AODP是菱形。
练 习
4、如图, 在△ABC中, AB=AC, 点M在边BC上, 过点M分别作AB、AC的平行线, 与AC、AB分别相交于点D、E. 当点M位于BC的什么位置时, 四边形AEMD是菱形 请给予证明.
证明：∵EM∥AC,DM∥AB
∴四边形AEMD是平行四边形
若EM=DM,则□AEMD是菱形
∵AB=AC, ∴ ∠B=∠C
又∵EM∥AC,DM∥AB
∴∠BEM=∠EMD=∠MDC
∠B=∠C, ∠BEM=∠CDM, EM=DM
在△BME和△CMD中
∴ △BME≌ △CDM
∴BM=CM
∴当M为BC的中点时，四边形AEMD是菱形
5、已知：如图，在□ABCD中，AD＝2AB，E、F在直线AB上，且AE＝AB＝BF，求证：CE⊥DF。
连MN图中有几个菱形。
练 习
提示：2CE⊥DF
6、已知：如图，Rt△ABC中，∠ACB＝90°，∠BAC＝60°，DE垂直平分BC，垂足为D，交AB于E，又点F在DE的延长线上，且AF＝CE。求证：四边形ACEF是菱形。
练 习
7、已知如图，在△ABC,∠ACB=900，AD是角平分线，点E、F分别在AB、AD上，且AE=AC，EF∥BC。
求证：四边形CDEF是菱形
O
1
2
A
C
B
D
E
F
练 习
.如图所示,两张宽度相同的矩形纸条交叉重叠在一起,重叠部分构成一个四边形ABCD.
请你认真分析:四边形ABCD是什么特殊四边形 证明你的结论.
小 结
1、菱形的判定定理的证明；
2、菱形与平行四边形的关系。
作 业
1、评价手册。
2.BCXT.