9.4整式
图片预览







文档简介
(共24张PPT)
根据题意列代数式
1. 温度由t℃下降5 ℃后的温度是 ℃
2. 小明想为希望工程捐款,每月从零用钱中贮存x元钱,一年后小明共存款 元
3. 某饭店要定做一批圆桌桌面,已知桌面的半径为r厘米,则每个桌面的面积是 平方厘米;
4.若一个三角形的一边长为5,这条边上的高为h,则这个三角形的面积为 ;
5.一个塑料三角尺如图1一2 所示,
阴影部分所占的面积是 _____________;
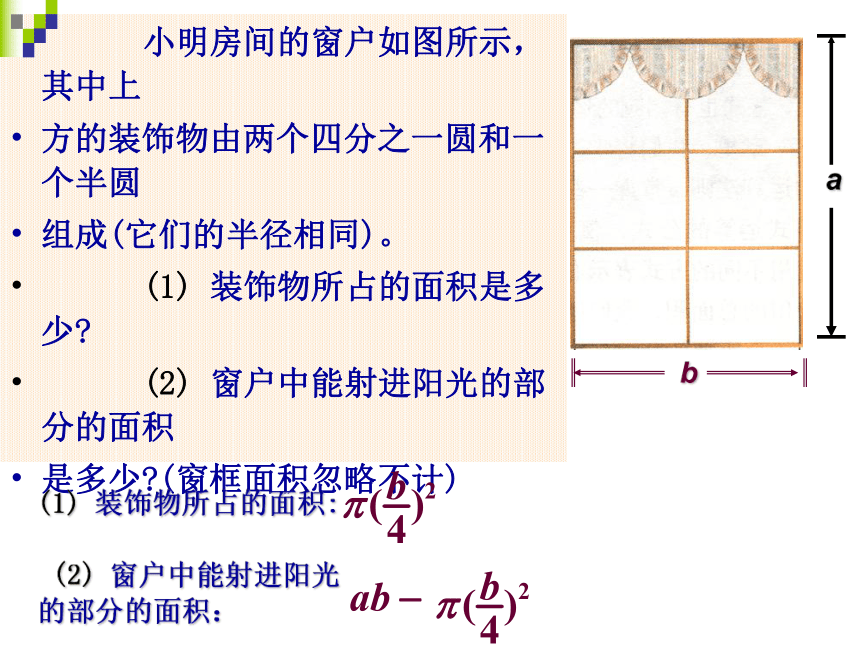
小明房间的窗户如图所示,其中上
方的装饰物由两个四分之一圆和一个半圆
组成(它们的半径相同)。
(1) 装饰物所占的面积是多少
(2) 窗户中能射进阳光的部分的面积
是多少 (窗框面积忽略不计)
b
a
(1) 装饰物所占的面积:
(2) 窗户中能射进阳光
的部分的面积:
你能将上述所列的代数式进行分类吗?
说说你分类的依据是什么?
都是由数与字母的乘积组成的,
这样的代数式叫做单项式
单独的一个数字或字母也是单项式
注 意
例1 判断下列各代数式是否是单项式.如果不是,请简要说明理由;
.
(1) (2) (3) (4)
观察单项式 、 、
有什么不同?
一个单项式中,所有字母的指数的和
叫做这个单项式的次数
观察单项式: 、 、 、
有什么不同?
单项式中的数字因数叫做这个单项式的
系数
注 意
*单独一个非零数 (常数项) 的次数是 0 。
单项式
系数
次数
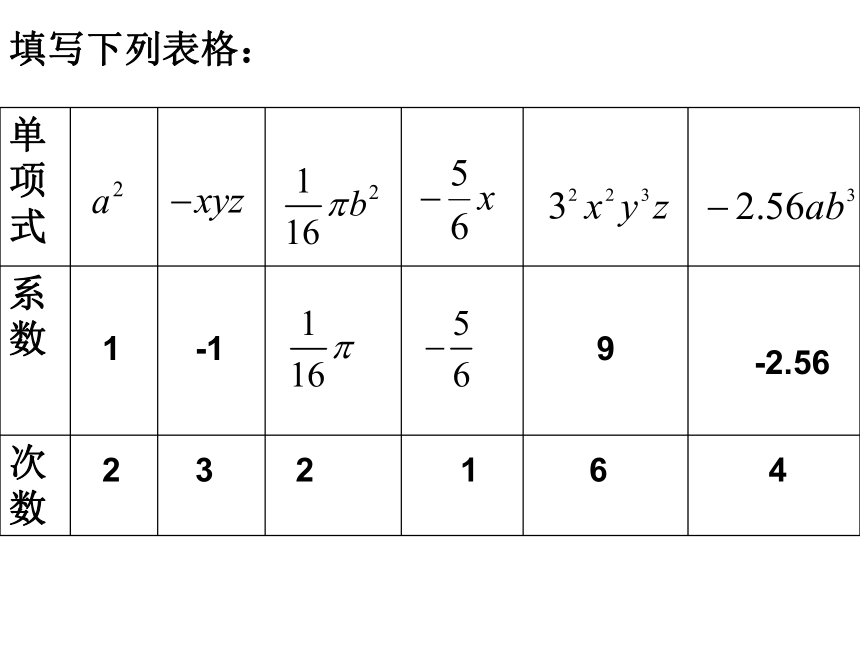
填写下列表格:
1
2
-1
3
2
1
9
6
-2.56
4
拓 展 练 习
1. 单项式m2n2的系数是____ ,次数是______, m2n2是____次单项式.
3. 如果 -5xym-2 为4次单项式, 则 m=____.
1
4
4
2. 的系数是_______,它是______次单项式
4.判断下列说法是否正确,正确的在括号内打“√”,不正确的打“×”.
(1)单项式m既没有系数也没有次数( )
(2)单项式5×105的系数是5 ( )
(3)-2006是单项式( )
(4)单项式 的系数是 ( )
一个多项式中,次数最高的项的次数,叫做这个多项式的次数。
由几个单项式的和组成的代数式叫做多项式,
例如
多项式中的每一个单项式,叫做多项的
项。
有 项、次数是 ;
是 次 项式
2
2
是 次 项式。
一
二
二
二
例2:指出下列多项式的项和次数.
(1)
(2)
解:
(1)多项式
的项有:
(2)多项式
的项有
1
次数是:4
次数是:3.
例3 指出下列多项式是几次几项式:
解:(1)
是一个三次三项式。
(2)
是一个四次三项式
(3)
(3)
是一个二次三项式
解题后的归纳
试将单项式、多项式、整式、代数式进行分类。
可使用下列两种方式之一:
代数式
整式
单项式
多项式
单项式和多项式统称
整式(integral expression).
(1)–1; (2)r; (3)
(4) ;(5) ;(6)
判断下列各代数式是否整式?
(7) ;
(8) ;
(9)
例4、关于x代数式3x + 4x – 2bx是四次二项式,试求a, b的值
解:
a+1
因为代数式的次数是四次
所以a + 1 = 4
所以a = 3
又因为代数式的项是二项
所以 – 2b =0即b=0
所以a=3, b=0
2
拓展提高:
3、当k为何值时,多项式
是四次多项式?
2、当m,n满足何条件时,多项式
是关于x的二次二项式?
1、多项式 是关于x的二次三项式,求m与n的差。
我们已经学习了多项式的概念,知道多项式是几个单项式的和。如多项式x +x+1就是单项式 的和。
你能解决以下问题吗?试一试
x ,+x,+1
问题1.如果交换多项式各项位置,所得到的多项式与原多项式是否相等?为什么?
问题2.任意交换x +x+1中各项的位置,可以得到几种不同的排列方式?请一一列举出来.
这样整齐的写法会为今后的计算带来方便。因而我们常常把一个多项式各项的位置按照其中某一个字母的指数大小顺序来排列.
多项式 按x的指数 的顺序排列
按x指数 的顺序排列 .
x +x+1
从大到小
1+x+ x
从小到大
降幂排列:把一个多项式按某个字母的指数按从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。
升幂排列:把一个多项式按某个字母的指数按从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。
二、 得出定义,揭示内涵
例5:把多项式 按x升幂排列.
解:
按x的升幂排列为:
重新排列多项式时,每一项一定要连同它的符号一起移动
注 意
例6:把多项式 重新排列.
(1) 按a升幂排列 ; (2)按a降幂排列
解:
(1) 按a升幂排列为
(2)按a降幂排列为
想一想:
如果是(1) 按b升幂排列 ; (2)按b降幂排列,结果回怎样呢?
根据题意列代数式
1. 温度由t℃下降5 ℃后的温度是 ℃
2. 小明想为希望工程捐款,每月从零用钱中贮存x元钱,一年后小明共存款 元
3. 某饭店要定做一批圆桌桌面,已知桌面的半径为r厘米,则每个桌面的面积是 平方厘米;
4.若一个三角形的一边长为5,这条边上的高为h,则这个三角形的面积为 ;
5.一个塑料三角尺如图1一2 所示,
阴影部分所占的面积是 _____________;
小明房间的窗户如图所示,其中上
方的装饰物由两个四分之一圆和一个半圆
组成(它们的半径相同)。
(1) 装饰物所占的面积是多少
(2) 窗户中能射进阳光的部分的面积
是多少 (窗框面积忽略不计)
b
a
(1) 装饰物所占的面积:
(2) 窗户中能射进阳光
的部分的面积:
你能将上述所列的代数式进行分类吗?
说说你分类的依据是什么?
都是由数与字母的乘积组成的,
这样的代数式叫做单项式
单独的一个数字或字母也是单项式
注 意
例1 判断下列各代数式是否是单项式.如果不是,请简要说明理由;
.
(1) (2) (3) (4)
观察单项式 、 、
有什么不同?
一个单项式中,所有字母的指数的和
叫做这个单项式的次数
观察单项式: 、 、 、
有什么不同?
单项式中的数字因数叫做这个单项式的
系数
注 意
*单独一个非零数 (常数项) 的次数是 0 。
单项式
系数
次数
填写下列表格:
1
2
-1
3
2
1
9
6
-2.56
4
拓 展 练 习
1. 单项式m2n2的系数是____ ,次数是______, m2n2是____次单项式.
3. 如果 -5xym-2 为4次单项式, 则 m=____.
1
4
4
2. 的系数是_______,它是______次单项式
4.判断下列说法是否正确,正确的在括号内打“√”,不正确的打“×”.
(1)单项式m既没有系数也没有次数( )
(2)单项式5×105的系数是5 ( )
(3)-2006是单项式( )
(4)单项式 的系数是 ( )
一个多项式中,次数最高的项的次数,叫做这个多项式的次数。
由几个单项式的和组成的代数式叫做多项式,
例如
多项式中的每一个单项式,叫做多项的
项。
有 项、次数是 ;
是 次 项式
2
2
是 次 项式。
一
二
二
二
例2:指出下列多项式的项和次数.
(1)
(2)
解:
(1)多项式
的项有:
(2)多项式
的项有
1
次数是:4
次数是:3.
例3 指出下列多项式是几次几项式:
解:(1)
是一个三次三项式。
(2)
是一个四次三项式
(3)
(3)
是一个二次三项式
解题后的归纳
试将单项式、多项式、整式、代数式进行分类。
可使用下列两种方式之一:
代数式
整式
单项式
多项式
单项式和多项式统称
整式(integral expression).
(1)–1; (2)r; (3)
(4) ;(5) ;(6)
判断下列各代数式是否整式?
(7) ;
(8) ;
(9)
例4、关于x代数式3x + 4x – 2bx是四次二项式,试求a, b的值
解:
a+1
因为代数式的次数是四次
所以a + 1 = 4
所以a = 3
又因为代数式的项是二项
所以 – 2b =0即b=0
所以a=3, b=0
2
拓展提高:
3、当k为何值时,多项式
是四次多项式?
2、当m,n满足何条件时,多项式
是关于x的二次二项式?
1、多项式 是关于x的二次三项式,求m与n的差。
我们已经学习了多项式的概念,知道多项式是几个单项式的和。如多项式x +x+1就是单项式 的和。
你能解决以下问题吗?试一试
x ,+x,+1
问题1.如果交换多项式各项位置,所得到的多项式与原多项式是否相等?为什么?
问题2.任意交换x +x+1中各项的位置,可以得到几种不同的排列方式?请一一列举出来.
这样整齐的写法会为今后的计算带来方便。因而我们常常把一个多项式各项的位置按照其中某一个字母的指数大小顺序来排列.
多项式 按x的指数 的顺序排列
按x指数 的顺序排列 .
x +x+1
从大到小
1+x+ x
从小到大
降幂排列:把一个多项式按某个字母的指数按从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。
升幂排列:把一个多项式按某个字母的指数按从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。
二、 得出定义,揭示内涵
例5:把多项式 按x升幂排列.
解:
按x的升幂排列为:
重新排列多项式时,每一项一定要连同它的符号一起移动
注 意
例6:把多项式 重新排列.
(1) 按a升幂排列 ; (2)按a降幂排列
解:
(1) 按a升幂排列为
(2)按a降幂排列为
想一想:
如果是(1) 按b升幂排列 ; (2)按b降幂排列,结果回怎样呢?
