人教版高一数学必修四 2.2 平面向量的线性运算课件课件(共19张PPT)
文档属性
| 名称 | 人教版高一数学必修四 2.2 平面向量的线性运算课件课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 501.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 00:00:00 | ||
图片预览




文档简介
2.2平面向量的线性运算
2.2.1向量加法运算
及其几何意义
复习回顾:
向量加法的定义:我们把求两个向量 和的运算,叫做向量的加法, 叫做 的和.
例2.长江两岸之间没有大桥的地方,常常通过轮渡进行运输.一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字);
(2)求船实际航行的速度的大小和方向(用与江水速度间的夹角表示,精确到度).
变式:
在静水中船速为20m/min,水流速度为10m/min,若船从岸边出发,垂直于水流航线到达对岸的,问船行进的方向是___________________________.
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
1、向量:
既有大小又有方向的量叫做向量
2、平行向量:
方向相同或相反的非零向量叫做平行向量
3、相等向量:
长度相等且方向相同的向量叫做相等向量
节引言:
数能进行运算,因为有了运算而使数的威力无穷。与数的运算类比,向量是否也能进行运算呢?人们从向量的物理背景和数的运算中得到启发,引进了向量的运算。
下面我们学习向量的线性运算。
向量加法运算及其几何意义
向量加法运算及其几何意义
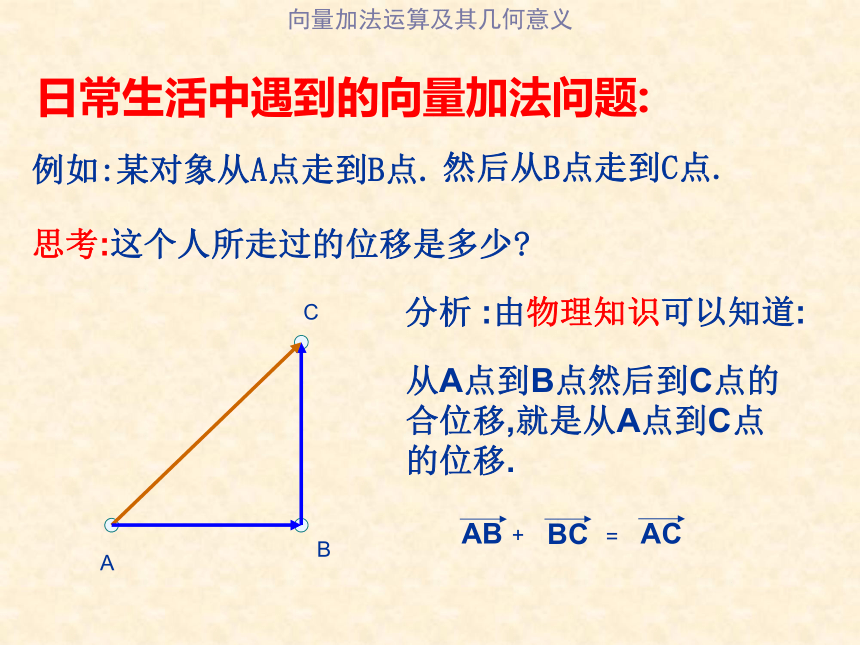
例如:某对象从A点走到B点.
日常生活中遇到的向量加法问题:
然后从B点走到C点.
思考:这个人所走过的位移是多少?
A
B
C
分析 :由物理知识可以知道:
从A点到B点然后到C点的
合位移,就是从A点到C点
的位移.
AB
BC
AC
=
+
向量加法运算及其几何意义
F1
F2
F
E
O
O
E
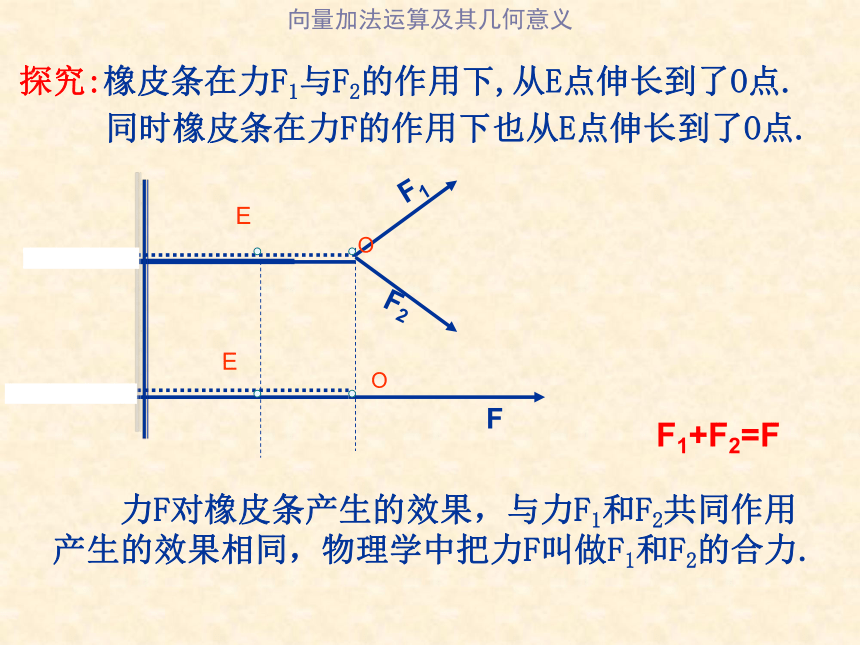
探究:橡皮条在力F1与F2的作用下,从E点伸长到了O点.
同时橡皮条在力F的作用下也从E点伸长到了O点.
F1+F2=F
力F对橡皮条产生的效果,与力F1和F2共同作用产生的效果相同,物理学中把力F叫做F1和F2的合力.
向量加法运算及其几何意义
F1
F2
F1
F2
F
F
E
O
O
E
思考:合力F与力F1、F2有怎样的关系?
力F在以F1、F2为邻边的平行四边形的对角线上,并且大小等于平行四边形对角线的长.
向量加法运算及其几何意义
两个向量的和仍然是一个向量.
向量加法运算及其几何意义
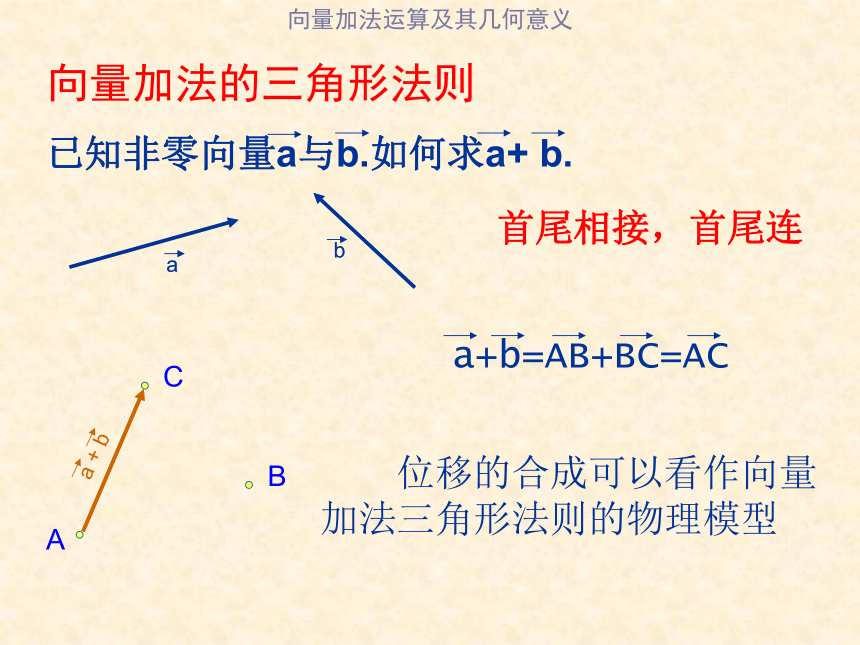
已知非零向量a与b.如何求a+ b.
首尾相接,首尾连
向量加法的三角形法则
A
C
a
b
a
b
B
a + b
a+b=AB+BC=AC
位移的合成可以看作向量加法三角形法则的物理模型
向量加法运算及其几何意义
向量加法的平行四边形法则
a
b
a
b
B
O
A
C
a + b
起点相同,连对角
力的合成可以看作向量加法平行四边形法则的物理模型
向量加法运算及其几何意义
例1.如图,已知向量 ,求作向量 。
则
作法1:在平面内任取一点O,
作 , ,
例题讲解:
o·
A
B
o·
A
B
C
作法2:在平面内任取一点O,
作 , ,
连结OC,则
以 为
邻边作 ,
OACB
向量加法运算及其几何意义
思考:
如图,当在数轴上表示两个共线向量时,它们的加法与数的加法有什么关系?
(1)
(2)
A
B
C
B
C
A
向量加法运算及其几何意义
当向量 不共线时,和向量的长度 与向量
的长度和 之间的大小关系如何?
三角形的两边之和大于第三边
综合以上探究我们可得结论:
向量加法运算及其几何意义
(1)
(2)
(4)
课堂练习:
一、用三角形法则求向量的和
(2)
二、用平行四边形法则求向量的和
向量加法运算及其几何意义
数的加法满足交换律与结合律,即对任意a,b∈R,有a+b=b+a, (a+b)+c=a+(b+c)
任意向量 的加法是否也满足交换律与结合律?
探究:
C
A
B
D
因为 AC = AB + BC = a + b
所以
r r
a
b
+
=
向量加法运算及其几何意义
A
B
C
D
( )
( )
向量的加法满足交换律和结合律.
向量加法运算及其几何意义
学以致用:
向量加法运算及其几何意义
D
5
C
解:
如图,设 表示水流的速度, 表示渡船的速度,
表示渡船实际过江的速度.(由平行四边形法则可以得到)
≈5.4
答:船实际航行速度的大小约为5.4km/h,方向与水的流速间的夹角约为680
分析:
向量加法在实际生活中的应用,本例应解决的问题是向量模的大小及向量的方向
向量加法运算及其几何意义
A
B
C
D
向量 表示水流速度, 表示船行进方向, 表示船实际行走路线,垂直于水流方向,所以∠DAC即为所求
方向与水的流速间的夹角为120o
向量加法运算及其几何意义
课堂练习:
A
B
C
D
E
(1)根据图示填空:
14
向量加法运算及其几何意义
归纳小结:
1、一个概念: 向量的加法
2、两个法则: 向量加法的三角形法则和平行四边形法则
3、两条运算律: 向量加法的交换律
结合律
+
+
=
+
+
( )
=
+
+
( )
知识方面:
+
+
=
=
数学思想方法方面:
1、具体与抽象的数学思维方法,
2、类比的思想方法
作业:
课本91页习题2.2A组2、3、4.(1)(2)(3)
2.2.1向量加法运算
及其几何意义
复习回顾:
向量加法的定义:我们把求两个向量 和的运算,叫做向量的加法, 叫做 的和.
例2.长江两岸之间没有大桥的地方,常常通过轮渡进行运输.一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字);
(2)求船实际航行的速度的大小和方向(用与江水速度间的夹角表示,精确到度).
变式:
在静水中船速为20m/min,水流速度为10m/min,若船从岸边出发,垂直于水流航线到达对岸的,问船行进的方向是___________________________.
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
1、向量:
既有大小又有方向的量叫做向量
2、平行向量:
方向相同或相反的非零向量叫做平行向量
3、相等向量:
长度相等且方向相同的向量叫做相等向量
节引言:
数能进行运算,因为有了运算而使数的威力无穷。与数的运算类比,向量是否也能进行运算呢?人们从向量的物理背景和数的运算中得到启发,引进了向量的运算。
下面我们学习向量的线性运算。
向量加法运算及其几何意义
向量加法运算及其几何意义
例如:某对象从A点走到B点.
日常生活中遇到的向量加法问题:
然后从B点走到C点.
思考:这个人所走过的位移是多少?
A
B
C
分析 :由物理知识可以知道:
从A点到B点然后到C点的
合位移,就是从A点到C点
的位移.
AB
BC
AC
=
+
向量加法运算及其几何意义
F1
F2
F
E
O
O
E
探究:橡皮条在力F1与F2的作用下,从E点伸长到了O点.
同时橡皮条在力F的作用下也从E点伸长到了O点.
F1+F2=F
力F对橡皮条产生的效果,与力F1和F2共同作用产生的效果相同,物理学中把力F叫做F1和F2的合力.
向量加法运算及其几何意义
F1
F2
F1
F2
F
F
E
O
O
E
思考:合力F与力F1、F2有怎样的关系?
力F在以F1、F2为邻边的平行四边形的对角线上,并且大小等于平行四边形对角线的长.
向量加法运算及其几何意义
两个向量的和仍然是一个向量.
向量加法运算及其几何意义
已知非零向量a与b.如何求a+ b.
首尾相接,首尾连
向量加法的三角形法则
A
C
a
b
a
b
B
a + b
a+b=AB+BC=AC
位移的合成可以看作向量加法三角形法则的物理模型
向量加法运算及其几何意义
向量加法的平行四边形法则
a
b
a
b
B
O
A
C
a + b
起点相同,连对角
力的合成可以看作向量加法平行四边形法则的物理模型
向量加法运算及其几何意义
例1.如图,已知向量 ,求作向量 。
则
作法1:在平面内任取一点O,
作 , ,
例题讲解:
o·
A
B
o·
A
B
C
作法2:在平面内任取一点O,
作 , ,
连结OC,则
以 为
邻边作 ,
OACB
向量加法运算及其几何意义
思考:
如图,当在数轴上表示两个共线向量时,它们的加法与数的加法有什么关系?
(1)
(2)
A
B
C
B
C
A
向量加法运算及其几何意义
当向量 不共线时,和向量的长度 与向量
的长度和 之间的大小关系如何?
三角形的两边之和大于第三边
综合以上探究我们可得结论:
向量加法运算及其几何意义
(1)
(2)
(4)
课堂练习:
一、用三角形法则求向量的和
(2)
二、用平行四边形法则求向量的和
向量加法运算及其几何意义
数的加法满足交换律与结合律,即对任意a,b∈R,有a+b=b+a, (a+b)+c=a+(b+c)
任意向量 的加法是否也满足交换律与结合律?
探究:
C
A
B
D
因为 AC = AB + BC = a + b
所以
r r
a
b
+
=
向量加法运算及其几何意义
A
B
C
D
( )
( )
向量的加法满足交换律和结合律.
向量加法运算及其几何意义
学以致用:
向量加法运算及其几何意义
D
5
C
解:
如图,设 表示水流的速度, 表示渡船的速度,
表示渡船实际过江的速度.(由平行四边形法则可以得到)
≈5.4
答:船实际航行速度的大小约为5.4km/h,方向与水的流速间的夹角约为680
分析:
向量加法在实际生活中的应用,本例应解决的问题是向量模的大小及向量的方向
向量加法运算及其几何意义
A
B
C
D
向量 表示水流速度, 表示船行进方向, 表示船实际行走路线,垂直于水流方向,所以∠DAC即为所求
方向与水的流速间的夹角为120o
向量加法运算及其几何意义
课堂练习:
A
B
C
D
E
(1)根据图示填空:
14
向量加法运算及其几何意义
归纳小结:
1、一个概念: 向量的加法
2、两个法则: 向量加法的三角形法则和平行四边形法则
3、两条运算律: 向量加法的交换律
结合律
+
+
=
+
+
( )
=
+
+
( )
知识方面:
+
+
=
=
数学思想方法方面:
1、具体与抽象的数学思维方法,
2、类比的思想方法
作业:
课本91页习题2.2A组2、3、4.(1)(2)(3)
