配方法解一元二次方程

(共14张PPT)
用配方法---
解一元二次方程
一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
例1.用开平方法解下列方程:
(1)3x2－27=0;
(2)(2x－3)2=7
（１）方程　　　　的根是
（２）方程　　　　　的根是　　
（3） 方程 　　　　的根是
2. 选择适当的方法解下列方程：
（1）x2－ 81＝0 （2） x2 ＝50
(3)(x＋1)2=4 (4)x2＋2 x＋5=0
X1=0.5, x2=－0.5
X1＝3， x2＝—3
X1＝2， x2＝－1
解下列方程:
1.x2 – 2 = 0;
2.16x2 – 25 = 0;
3.(x + 1)2 – 4 = 0;
4.12(2 - x)2 - 9 = 0;
5.x2-144=0 ;
6. y2-7=0;
7.x2+5=0 ;
8.(x + 3)2 = 2;
9.(x+3) =6 ;
随堂练习
1
8.(x + 3)2 = 2;
9.(x+3) =6 ;
10.16x -49=0 ;
11. (2x+3) =5 ;
12. 2x =128 ;
13. (x+1) -12= 0 ;
14. x2 - 10x +25 = 0
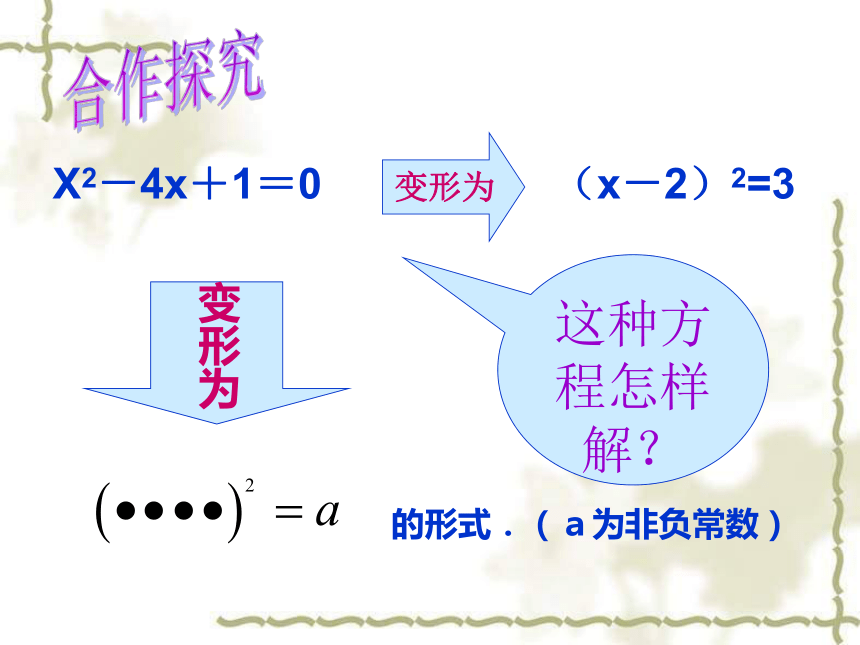
这种方程怎样解？
变形为
的形式．（ａ为非负常数）
变形为
X2－4x＋1＝0
（x－2）2=3
把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
(1)x2＋8x＋ =(x＋4)2
(2)x2－4x＋ =(x－ )2
(3)x2－___x＋ 9 =(x－ )2
配方时, 等式两边同时加上的是一次项系数一半的平方
16
6
3
4
2
例2：用配方法解下列方程
(1)x2＋6x=1
(2)x2=6－5x
x2 +6x =1;
49x2 - 42x – 1 = 0.
用配方法解一元二次方程的步骤:
移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.
(2) －x2＋4x－3=0
(1) x2＋12x =－9
练习3：用配方法解下列方程：
4. 用配方法说明：不论k取何实数，多项式
k2－3k＋5的值必定大于零.
独立
作业
2. 解下列方程:
(1).x2 +12x+ 25 = 0;
(2).x2 +4x =1 0;
(3).x 2 –6x =11;
(4). x2 –2x-4 = 0.
独立
作业
１．根据题意，列出方程：
1.如图,在一块长35m,宽26m矩形地面上,修建同样宽的两条互相垂直的道路,剩余部分栽种花草,在使剩余部分的面积为850m2,道路的宽应是多少？
解：设道路的宽为 x m，根据题意得
(35-x) (26-x) ＝850.
即
x2 - 61x+60 ＝0.
35m
26m
解这个方程,得
x1 ＝1;
x2 ＝60(不合题意,舍去).
答:道路的宽应为1m.
思考：先用配方法解下列方程：
（1） x2－2x－1＝0 （2） x2－2x＋4＝0
（3） x2－2x＋1＝0
然后回答下列问题：
（1）你在求解过程中遇到什么问题？你是怎样处理所遇到的问题的？
（2）对于形如x2＋px＋q＝0这样的方程，在什么条件下才有实数根？
1.一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
2.把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
注意:配方时, 等式两边同时加上的是一次项
系数一半的平方.