28.4垂径定理-冀教版九年级数学上册课件(33张)
文档属性
| 名称 | 28.4垂径定理-冀教版九年级数学上册课件(33张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 10:12:54 | ||
图片预览




文档简介
(共43张PPT)
28.4
垂径定理
第二十八章
圆
冀教版九上
●
学
习
目
标
1.探究垂径定理及其推论.
2.会用垂径定理及其推论解决问题.
创设情境,引入新课
如图是某公园的一个圆拱形门,路面AB的宽为2米,净高CD为5米,则圆拱形门所在圆的半径是多少米?
A
B
C
D
创设情境,引入新课
A
B
C
D
●
O
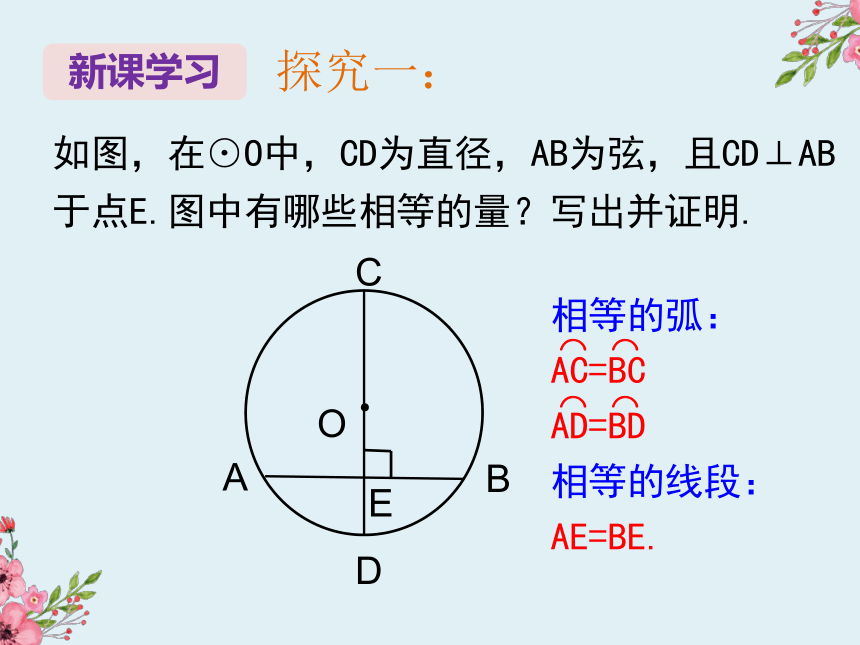
小红:为什么AD等于AB的一半呢?
小明:呃......
你能帮小明证明吗?
小明:取圆心O,连接OA,设半径为x,则AO=x,
OD=5-x,由AB=2,得AD=
=1,在Rt△AOD中,由勾股定理可得:
解得x=2.6米.
新课学习
如图,在⊙O中,CD为直径,AB为弦,且CD⊥AB于点E.图中有哪些相等的量?写出并证明.
A
O
B
C
●
D
E
探究一:
相等的弧:AC=BC
AD=BD
相等的线段:AE=BE.
⌒
⌒
⌒
⌒
新课学习
A
O
B
C
●
D
E
圆是轴对称图形,沿直径CD所在的直线折叠,两旁的部分会重合,则点A与点B重合,因此AE=BE,AD=BD,AC=BC.
⌒
⌒
⌒
⌒
小美
新课学习
A
O
B
C
●
D
E
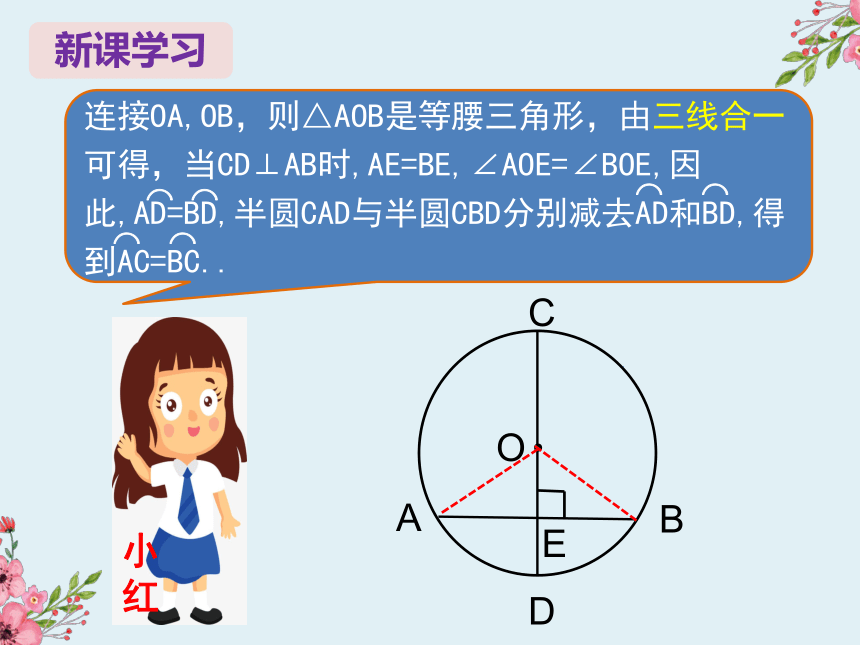
小红
连接OA,OB,则△AOB是等腰三角形,由三线合一可得,当CD⊥AB时,AE=BE,∠AOE=∠BOE,因此,AD=BD,半圆CAD与半圆CBD分别减去AD和BD,得到AC=BC..
⌒
⌒
⌒
⌒
⌒
⌒
新课学习
A
O
B
C
●
D
E
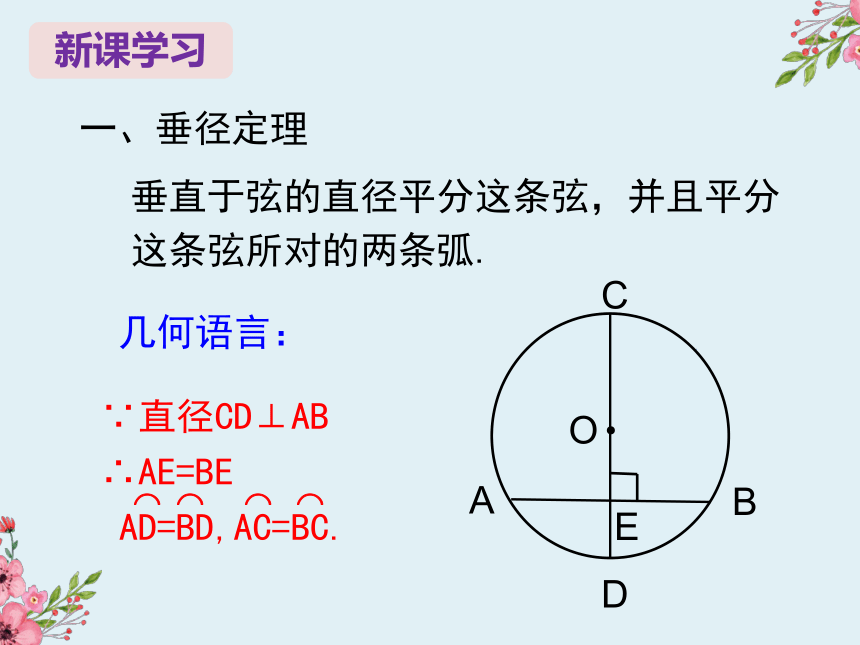
一、垂径定理
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
几何语言:
∵直径CD⊥AB
∴AE=BE
AD=BD,AC=BC.
⌒
⌒
⌒
⌒
新课学习
A
O
B
C
●
D
E
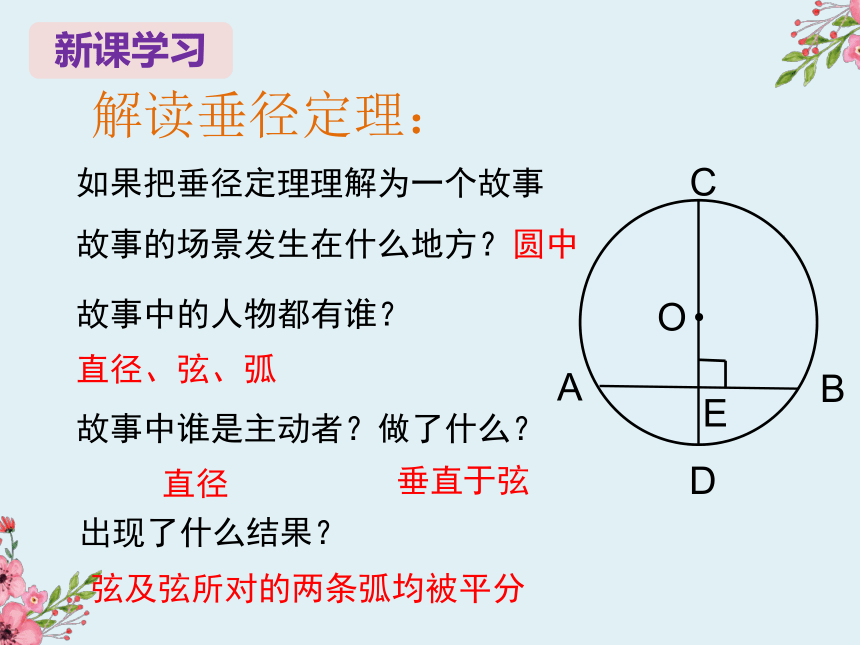
解读垂径定理:
如果把垂径定理理解为一个故事
故事的场景发生在什么地方?
圆中
故事中的人物都有谁?
直径、弦、弧
故事中谁是主动者?做了什么?
直径
垂直于弦
出现了什么结果?
弦及弦所对的两条弧均被平分
巩固小练习
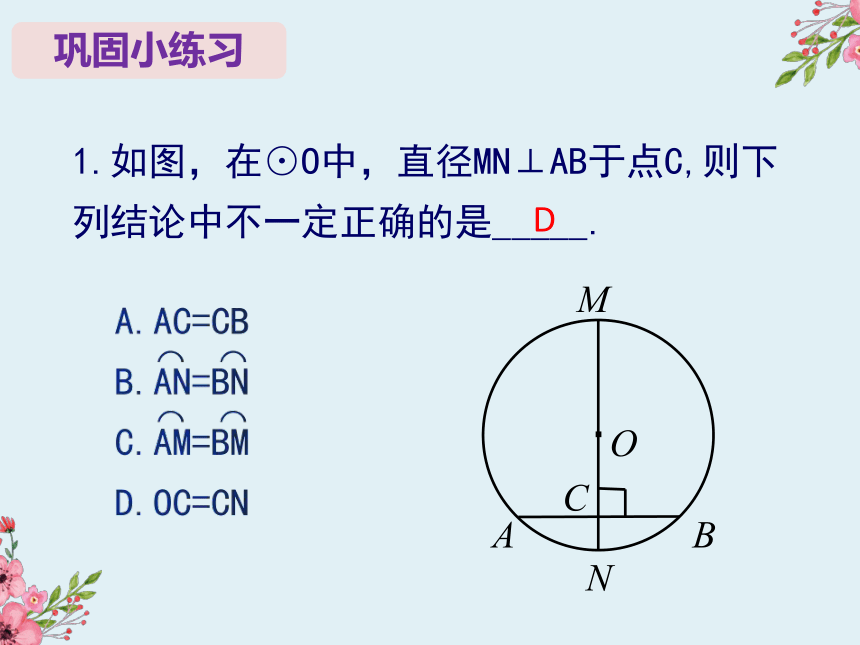
1.如图,在⊙O中,直径MN⊥AB于点C,则下列结论中不一定正确的是_____.
D
·
O
A
B
C
N
M
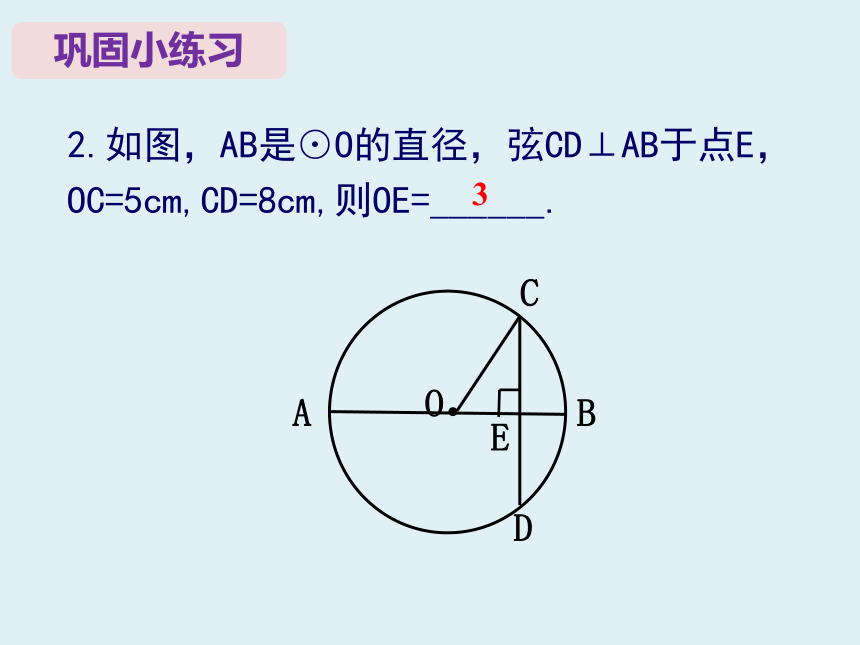
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,
OC=5cm,CD=8cm,则OE=______.
3
巩固小练习
B
A
C
D
O
●
E
新课学习
探究二
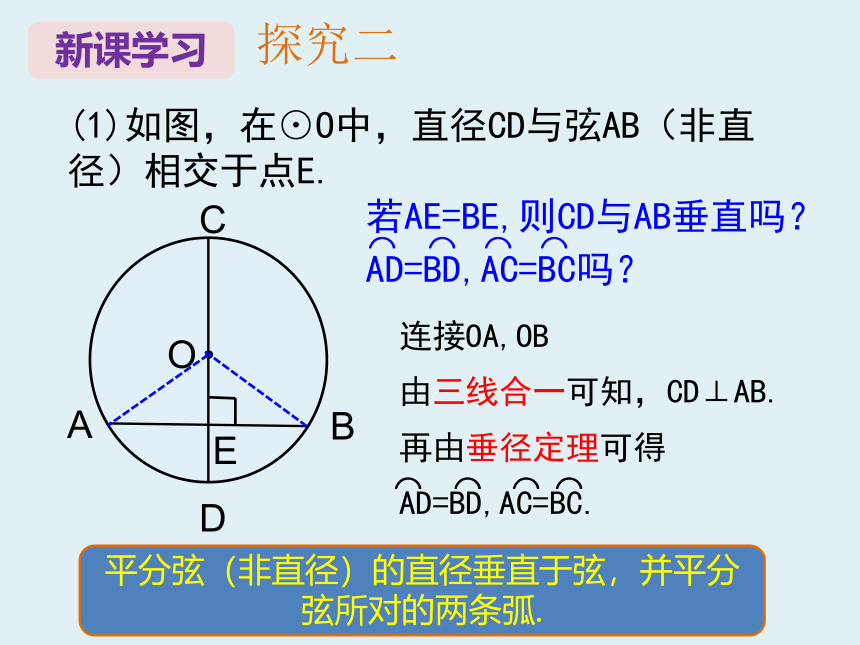
(1)如图,在⊙O中,直径CD与弦AB(非直径)相交于点E.
A
O
B
C
●
D
E
若AE=BE,则CD与AB垂直吗?AD=BD,AC=BC吗?
⌒
⌒
⌒
⌒
连接OA,OB
由三线合一可知,CD⊥AB.
再由垂径定理可得AD=BD,AC=BC.
⌒
⌒
⌒
⌒
平分弦(非直径)的直径垂直于弦,并平分弦所对的两条弧.
新课学习
探究二
(2)如图,在⊙O中,直径CD与弦AB(非直径)相交于点E.
A
O
B
C
●
D
E
若AD=BD,则AE=BE,CD⊥AB吗?
⌒
⌒
连接OA,OB,由AD=BD
可推出∠AOD=∠BOD
由三线合一可知,
AE=BE,CD⊥AB.
⌒
⌒
平分弧的直径垂直平分弧所对的弦.
在⊙O中,设直径CD与弦AB(非直径)相交于点E.若把AE=BE,CD⊥AB,AD=BD中的一项作为条件,则可得另外两项结论.
⌒
⌒
结论
能去掉吗?
A
O
B
C
●
D
(E)
如图,当AB是直径时,CD平分AB,但CD与AB并不垂直.
不能
巩固小练习
下列命题:
①平分弦所对的两条弧的直线必垂直于弦;
②垂直于弦的直线平分弦;
③平分弦的直径平分弦所对的弧;
④与直径不垂直的弦不能被该直径平分;
⑤过一条弦所对的两条弧的中点的直线一定过圆心.
其中正确的是__________.
①⑤
例1.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=16,OE=6,求⊙O的半径.
典例精析
B
A
C
D
O
●
E
解:连接OC
∵CD⊥AB
∴⊙O的半径为10.
AB=20
CD的长.
解:连接OC,
AO=10,CD=16
BE的长.
解:连接OC
∵CD⊥AB
∴BE=OB-OE=10-6=4
出现过圆心与弦垂直的线即可
例1.(变式一)如图,⊙O的半径为5,弦AB=6,求圆心O到弦CD的距离.
典例精析
B
A
O
●
解:过点O做OC⊥AB于点C,连接OA,
C
∴圆心O到弦CD的距离为4.
例1.(变式二)如图,CD为⊙O的直径,AB为弦,且AB⊥CD于点E.若ED=2,AB=8.求CD的长.
典例精析
解:连接OA,设⊙O的半径为r
∵AB⊥CD
解得,r=5
·
O
A
B
E
D
C
∴CD=2r=10
什么情况用方程?
直角三角形中只有一条边是已知的.
总结提升
利用垂径定理解决问题的基本图形
图中直角三角形的构成
B
A
C
O
●
斜边:
直角边:
半径
弦的一半
弦心距
在圆中求半径、弦长、弦心距最常用的方法
总结提升
利用垂径定理解决问题的基本图形
直角三角形中
B
A
C
O
●
已知两边
只知一边
用勾股定理直接求第三边
做弦心距、连半径是最常做的辅助线
需要用到勾股方程
典例精析
·
O
A
B
C
D
E
F
分析:已知中出现直径,从“直径所对的圆周角是直角”角度考虑.
例2.已知:如图,BC为⊙O的直径,BF为弦,A为BF的中点,AD⊥BC与点D,AD和BF相交于点E.求证:AE=BE.
⌒
典例精析
·
O
A
B
C
D
E
F
连接AB,AC
AB是⊙O的直径
∠ABC=90°
AD⊥BC
∠BAE=∠ACB
点A为BF的中点
⌒
ABE=∠ACB
ABE=∠BAE
AE=BE
构造直径所对的圆周角
典例精析
例2.已知:如图,BC为⊙O的直径,BF为弦,A为BF的中点,AD⊥BC与点D,AD和BF相交于点E.求证:AE=BE.
·
O
A
B
C
D
E
F
分析:已知中出现直径及垂直,从“垂径定理”角度考虑.
典例精析
·
O
A
B
C
D
E
F
M
延长AE与⊙O交于点M,连接AE
AD⊥BC
AB=MB
⌒
⌒
AB=AF
⌒
⌒
ABE=∠BAE
AE=BE
补全垂径定理的基本图形,使问题更易于解决
点A为BF的中点
⌒
总结提升
已知条件中出现直径时,最常用到的知识点
1.直径所对的圆周角是直角.
2.垂径定理.
巩固练习
1.如图,在平面直角坐标系中,以点P为圆心的圆与x轴交于A,B两点,已知P(4,2)和A(2,0).则点B的坐标是________.
y
x
P●
O
B
A
(6,0)
巩固练习
2.如图,OA为⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交与点D,求证:D为AB的中点.
·
·
D
O
C
B
A
答案:
连接OD
∵OA为⊙C的直径
∴OD⊥AB
∴AD=BD
即D为AB的中点
(直径所对的圆周角是直角)
(垂径定理)
提升小练习
A
B
C
(1)求BC的长度.
1.如图,△ABC是某住宅小区的一块三角形的绿化地.已知AB长为
m,∠B=45°,∠C的正切值为2.
M
BC=16+8=24
答案:
提升小练习
A
B
C
·
O
(2)若将绿化地改造为如图所示的⊙O,⊙O过A,C,并与BC交于点D,如果点A是优弧DAC的中点,求⊙O的半径.
D
1.如图,△ABC是某住宅小区的一块三角形的绿化地.已知AB长为
m,∠B=45°,∠C的正切值为2.
N
连接AO并延长交⊙O于点N.连接OC.
由点A是弧CAD的中点,得AN⊥BC.
r=10
答案:
提升小练习
2.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于C.若AP=8,PB=2,则PC的长是______.
·
O
A
B
C
P
4
D
答案:
延长CP交⊙O于点D,连接AD,BC,可得△PDA∽△PCB.
可计算出PC=4
提升小练习
3.如图,点P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于B,C两点,若⊙O的半径为3,OP=
,则弦BC的最大值是______.
·
O
A
B
C
P
●
答案:
M
过点O作OM⊥AB于点M,则BC=2OM,因此当OM最大时,BC最大.
当点M与P重合时,OM=OP时,OM最大.
课堂小结
垂径定理
1.关于直径、弦(非直径)、弦所对的弧之间的关系.
常用辅助线
连半径
过圆心做弦的垂线
构造直角三角形
同学们再见
28.4
垂径定理
第二十八章
圆
冀教版九上
●
学
习
目
标
1.探究垂径定理及其推论.
2.会用垂径定理及其推论解决问题.
创设情境,引入新课
如图是某公园的一个圆拱形门,路面AB的宽为2米,净高CD为5米,则圆拱形门所在圆的半径是多少米?
A
B
C
D
创设情境,引入新课
A
B
C
D
●
O
小红:为什么AD等于AB的一半呢?
小明:呃......
你能帮小明证明吗?
小明:取圆心O,连接OA,设半径为x,则AO=x,
OD=5-x,由AB=2,得AD=
=1,在Rt△AOD中,由勾股定理可得:
解得x=2.6米.
新课学习
如图,在⊙O中,CD为直径,AB为弦,且CD⊥AB于点E.图中有哪些相等的量?写出并证明.
A
O
B
C
●
D
E
探究一:
相等的弧:AC=BC
AD=BD
相等的线段:AE=BE.
⌒
⌒
⌒
⌒
新课学习
A
O
B
C
●
D
E
圆是轴对称图形,沿直径CD所在的直线折叠,两旁的部分会重合,则点A与点B重合,因此AE=BE,AD=BD,AC=BC.
⌒
⌒
⌒
⌒
小美
新课学习
A
O
B
C
●
D
E
小红
连接OA,OB,则△AOB是等腰三角形,由三线合一可得,当CD⊥AB时,AE=BE,∠AOE=∠BOE,因此,AD=BD,半圆CAD与半圆CBD分别减去AD和BD,得到AC=BC..
⌒
⌒
⌒
⌒
⌒
⌒
新课学习
A
O
B
C
●
D
E
一、垂径定理
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
几何语言:
∵直径CD⊥AB
∴AE=BE
AD=BD,AC=BC.
⌒
⌒
⌒
⌒
新课学习
A
O
B
C
●
D
E
解读垂径定理:
如果把垂径定理理解为一个故事
故事的场景发生在什么地方?
圆中
故事中的人物都有谁?
直径、弦、弧
故事中谁是主动者?做了什么?
直径
垂直于弦
出现了什么结果?
弦及弦所对的两条弧均被平分
巩固小练习
1.如图,在⊙O中,直径MN⊥AB于点C,则下列结论中不一定正确的是_____.
D
·
O
A
B
C
N
M
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,
OC=5cm,CD=8cm,则OE=______.
3
巩固小练习
B
A
C
D
O
●
E
新课学习
探究二
(1)如图,在⊙O中,直径CD与弦AB(非直径)相交于点E.
A
O
B
C
●
D
E
若AE=BE,则CD与AB垂直吗?AD=BD,AC=BC吗?
⌒
⌒
⌒
⌒
连接OA,OB
由三线合一可知,CD⊥AB.
再由垂径定理可得AD=BD,AC=BC.
⌒
⌒
⌒
⌒
平分弦(非直径)的直径垂直于弦,并平分弦所对的两条弧.
新课学习
探究二
(2)如图,在⊙O中,直径CD与弦AB(非直径)相交于点E.
A
O
B
C
●
D
E
若AD=BD,则AE=BE,CD⊥AB吗?
⌒
⌒
连接OA,OB,由AD=BD
可推出∠AOD=∠BOD
由三线合一可知,
AE=BE,CD⊥AB.
⌒
⌒
平分弧的直径垂直平分弧所对的弦.
在⊙O中,设直径CD与弦AB(非直径)相交于点E.若把AE=BE,CD⊥AB,AD=BD中的一项作为条件,则可得另外两项结论.
⌒
⌒
结论
能去掉吗?
A
O
B
C
●
D
(E)
如图,当AB是直径时,CD平分AB,但CD与AB并不垂直.
不能
巩固小练习
下列命题:
①平分弦所对的两条弧的直线必垂直于弦;
②垂直于弦的直线平分弦;
③平分弦的直径平分弦所对的弧;
④与直径不垂直的弦不能被该直径平分;
⑤过一条弦所对的两条弧的中点的直线一定过圆心.
其中正确的是__________.
①⑤
例1.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=16,OE=6,求⊙O的半径.
典例精析
B
A
C
D
O
●
E
解:连接OC
∵CD⊥AB
∴⊙O的半径为10.
AB=20
CD的长.
解:连接OC,
AO=10,CD=16
BE的长.
解:连接OC
∵CD⊥AB
∴BE=OB-OE=10-6=4
出现过圆心与弦垂直的线即可
例1.(变式一)如图,⊙O的半径为5,弦AB=6,求圆心O到弦CD的距离.
典例精析
B
A
O
●
解:过点O做OC⊥AB于点C,连接OA,
C
∴圆心O到弦CD的距离为4.
例1.(变式二)如图,CD为⊙O的直径,AB为弦,且AB⊥CD于点E.若ED=2,AB=8.求CD的长.
典例精析
解:连接OA,设⊙O的半径为r
∵AB⊥CD
解得,r=5
·
O
A
B
E
D
C
∴CD=2r=10
什么情况用方程?
直角三角形中只有一条边是已知的.
总结提升
利用垂径定理解决问题的基本图形
图中直角三角形的构成
B
A
C
O
●
斜边:
直角边:
半径
弦的一半
弦心距
在圆中求半径、弦长、弦心距最常用的方法
总结提升
利用垂径定理解决问题的基本图形
直角三角形中
B
A
C
O
●
已知两边
只知一边
用勾股定理直接求第三边
做弦心距、连半径是最常做的辅助线
需要用到勾股方程
典例精析
·
O
A
B
C
D
E
F
分析:已知中出现直径,从“直径所对的圆周角是直角”角度考虑.
例2.已知:如图,BC为⊙O的直径,BF为弦,A为BF的中点,AD⊥BC与点D,AD和BF相交于点E.求证:AE=BE.
⌒
典例精析
·
O
A
B
C
D
E
F
连接AB,AC
AB是⊙O的直径
∠ABC=90°
AD⊥BC
∠BAE=∠ACB
点A为BF的中点
⌒
ABE=∠ACB
ABE=∠BAE
AE=BE
构造直径所对的圆周角
典例精析
例2.已知:如图,BC为⊙O的直径,BF为弦,A为BF的中点,AD⊥BC与点D,AD和BF相交于点E.求证:AE=BE.
·
O
A
B
C
D
E
F
分析:已知中出现直径及垂直,从“垂径定理”角度考虑.
典例精析
·
O
A
B
C
D
E
F
M
延长AE与⊙O交于点M,连接AE
AD⊥BC
AB=MB
⌒
⌒
AB=AF
⌒
⌒
ABE=∠BAE
AE=BE
补全垂径定理的基本图形,使问题更易于解决
点A为BF的中点
⌒
总结提升
已知条件中出现直径时,最常用到的知识点
1.直径所对的圆周角是直角.
2.垂径定理.
巩固练习
1.如图,在平面直角坐标系中,以点P为圆心的圆与x轴交于A,B两点,已知P(4,2)和A(2,0).则点B的坐标是________.
y
x
P●
O
B
A
(6,0)
巩固练习
2.如图,OA为⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交与点D,求证:D为AB的中点.
·
·
D
O
C
B
A
答案:
连接OD
∵OA为⊙C的直径
∴OD⊥AB
∴AD=BD
即D为AB的中点
(直径所对的圆周角是直角)
(垂径定理)
提升小练习
A
B
C
(1)求BC的长度.
1.如图,△ABC是某住宅小区的一块三角形的绿化地.已知AB长为
m,∠B=45°,∠C的正切值为2.
M
BC=16+8=24
答案:
提升小练习
A
B
C
·
O
(2)若将绿化地改造为如图所示的⊙O,⊙O过A,C,并与BC交于点D,如果点A是优弧DAC的中点,求⊙O的半径.
D
1.如图,△ABC是某住宅小区的一块三角形的绿化地.已知AB长为
m,∠B=45°,∠C的正切值为2.
N
连接AO并延长交⊙O于点N.连接OC.
由点A是弧CAD的中点,得AN⊥BC.
r=10
答案:
提升小练习
2.如图,点P为弦AB上的一点,连接OP,过点P作PC⊥OP,PC交⊙O于C.若AP=8,PB=2,则PC的长是______.
·
O
A
B
C
P
4
D
答案:
延长CP交⊙O于点D,连接AD,BC,可得△PDA∽△PCB.
可计算出PC=4
提升小练习
3.如图,点P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP,AO分别与⊙O交于B,C两点,若⊙O的半径为3,OP=
,则弦BC的最大值是______.
·
O
A
B
C
P
●
答案:
M
过点O作OM⊥AB于点M,则BC=2OM,因此当OM最大时,BC最大.
当点M与P重合时,OM=OP时,OM最大.
课堂小结
垂径定理
1.关于直径、弦(非直径)、弦所对的弧之间的关系.
常用辅助线
连半径
过圆心做弦的垂线
构造直角三角形
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
