28.5弧长和扇形面积的计算-冀教版九年级数学上册课件(31张)
文档属性
| 名称 | 28.5弧长和扇形面积的计算-冀教版九年级数学上册课件(31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 10:15:58 | ||
图片预览






文档简介
(共41张PPT)
28.5
弧长和扇形面积的计算
第二十八章
圆
冀教版九上
学
习
目
标
1.探究弧长、扇形面积的计算公式.
2.了解圆锥的相关概念,知道圆锥的侧
面与扇形的关系.
3.能灵活运用弧长、扇形面积的计算
公式进行计算.
创设情境,引入新课
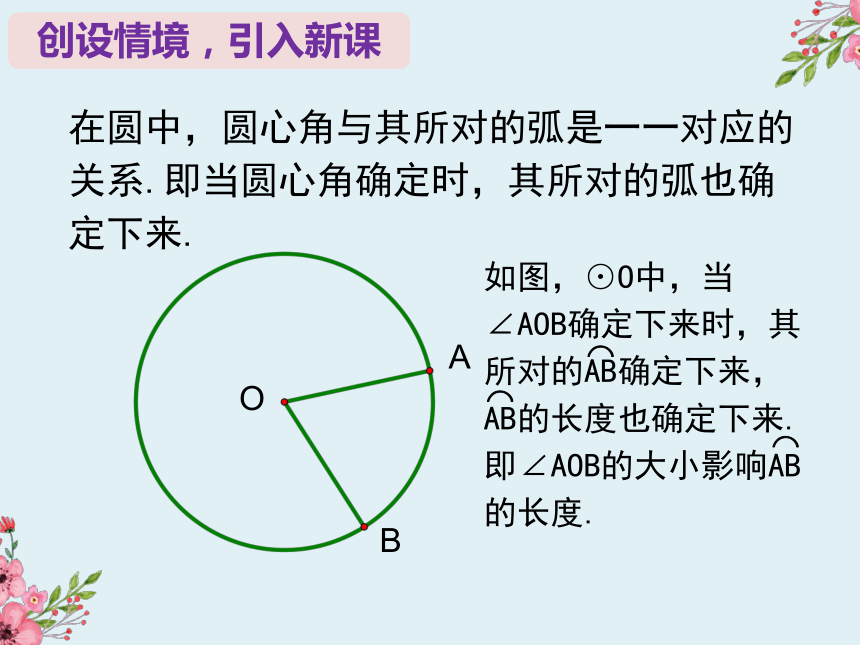
在圆中,圆心角与其所对的弧是一一对应的关系.即当圆心角确定时,其所对的弧也确定下来.
B
A
O
如图,⊙O中,当∠AOB确定下来时,其所对的AB确定下来,AB的长度也确定下来.
即∠AOB的大小影响AB的长度.
⌒
⌒
⌒
创设情境,引入新课
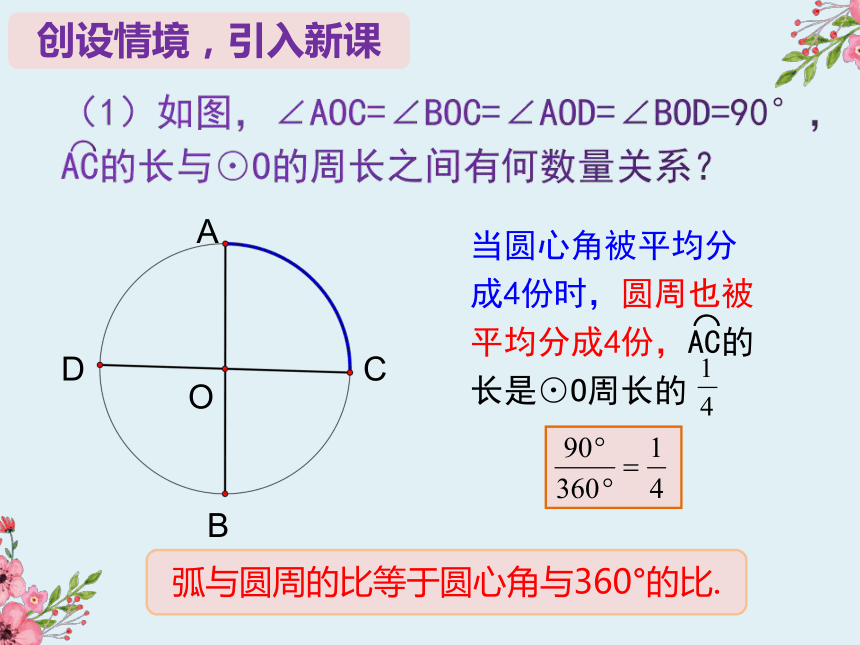
当圆心角被平均分成4份时,圆周也被平均分成4份,AC的长是⊙O周长的
⌒
D
B
C
A
O
弧与圆周的比等于圆心角与360°的比.
创设情境,引入新课
当圆心角被平均分成8份时,圆周也被平均分成8份,AE的长是⊙O周长的
⌒
B
A
C
D
O
●
E
F
M
N
弧与圆周的比等于圆心角与360°的比.
创设情境,引入新课
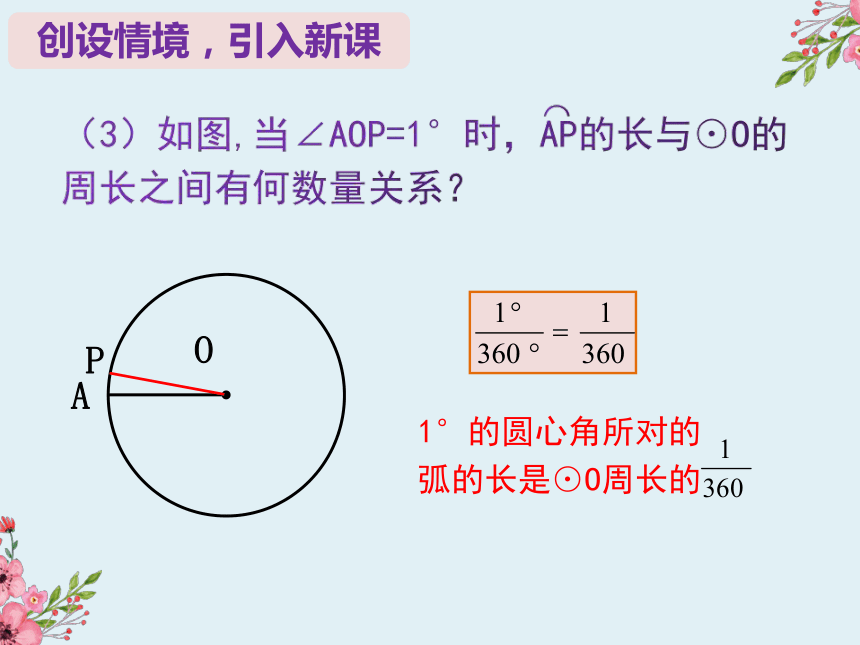
1°的圆心角所对的弧的长是⊙O周长的
A
O
●
P
创设情境,引入新课
10°的圆心角所对的弧长是圆周长的
类比:
32°的圆心角所对的弧长是圆周长的
117°的圆心角所对的弧长是圆周长的
200°的圆心角所对的弧长是圆周长的
n°的圆心角所对的弧长是圆周长的
新课学习
一、弧长公式
设圆的半径为r,n°的圆心角所对的弧的长为l.
影响弧长因素:
圆心角、半径
新课学习
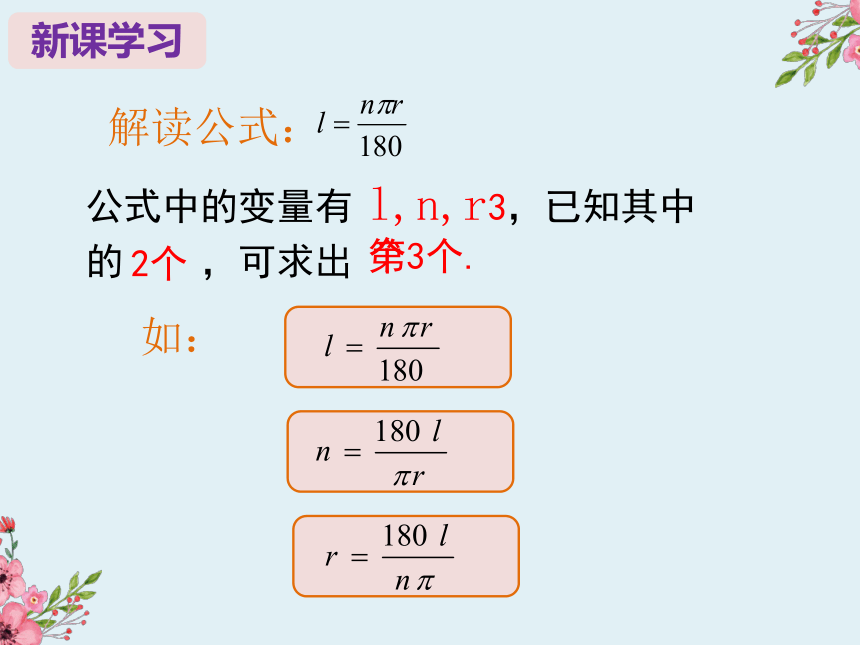
解读公式:
公式中的变量有
,已知其中的
,可求出
l,n,r3个
2个
第3个.
如:
巩固练习
1.在半径为6cm的圆中,120°的圆心角所对的弧长为______.
4π
2.已知圆中一段弧的长为240π,半径为180,求这个弧所对的圆心角的度数.
新课学习
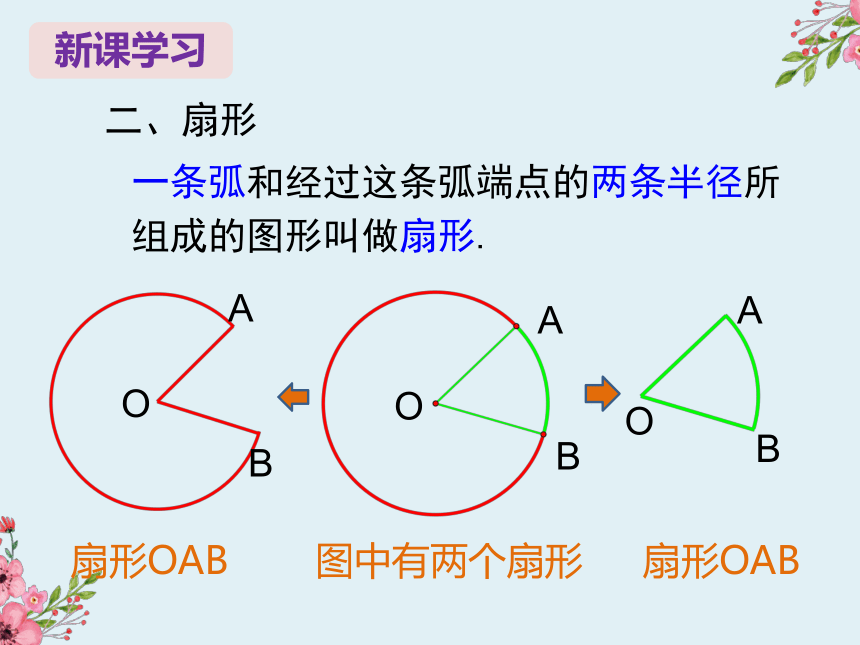
二、扇形
一条弧和经过这条弧端点的两条半径所组成的图形叫做扇形.
O
A
B
图中有两个扇形
O
A
B
O
A
B
扇形OAB
扇形OAB
巩固练习
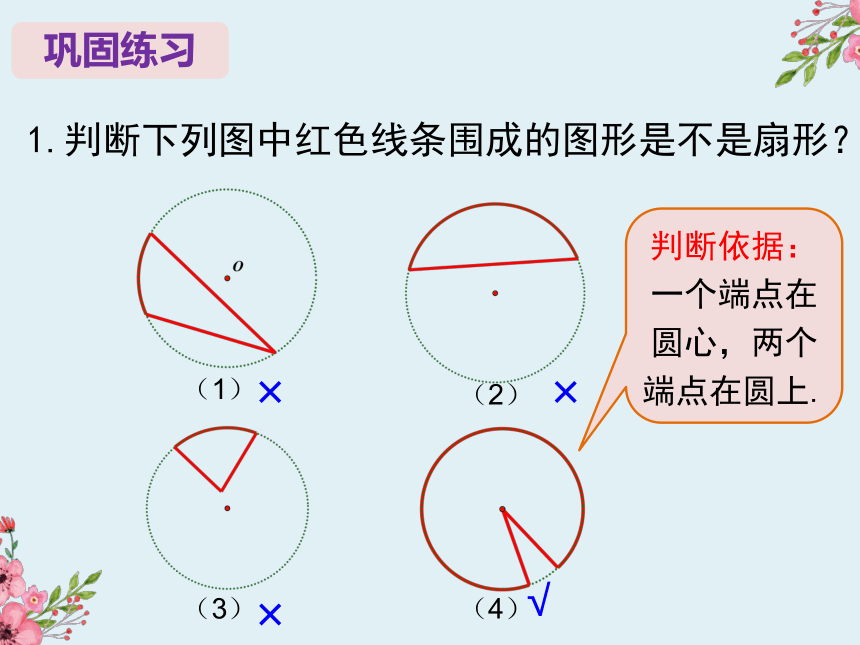
1.判断下列图中红色线条围成的图形是不是扇形?
(1)
(2)
(3)
(4)
√
×
×
×
判断依据:一个端点在圆心,两个端点在圆上.
新课学习
三、扇形的面积
O
A
B
在圆中,与弧长类似,当圆心角确定时,与其对应的扇形也确定下来.
扇形面积与圆的面积之比等于圆心角与360°之比.
如:
圆心角为1°的扇形面积是圆面积的
圆心角为50°的扇形面积是圆面积的
圆心角为n°的扇形面积是圆面积的
新课学习
三、扇形的面积
设圆的半径为r,圆心角为n°的扇形的面积为S.
影响扇形面积的因素:
圆心角、半径
新课学习
解读公式:
公式中的变量有
,已知其中的
,可求出
S,n,r共3个
2个
第3个.
如:
新课学习
思考:
当圆心角确定下来时,其对应的弧及扇形都是唯一的,即两者也是一一对应的,它们的数量关系会是怎样的呢?
影响扇形面积的因素:
弧长、半径
新课学习
解读公式:
公式中的变量有
,已知其中的
,可求出
S,l,r共3个
2个
第3个.
如:
总结
扇形的面积公式:
或
根据题中给出的已知条件,选择合适的计算公式.
例1.已知扇形的圆心角为120°,弧长为2π,
求扇形的面积.
典例精析
分析:
问题转化为:已知圆心角为120°,弧长为2π,求半径.
例1.已知扇形的圆心角为120°,弧长为2π,
求扇形的面积.
典例精析
答:扇形的面积为3π.
巩固练习
1.一个扇形的圆心角为100°,面积为15π,
则此扇形的半径长为_____.
2.一个扇形的半径为6,圆心角为120°,
则此扇形的面积为_____.
3.扇形的弧长为20π,面积为240π,
则此扇形的半径为_____.
12π
24
新课学习
四、圆锥及其相关概念
O
P
A
B
C
1.圆锥的母线:圆锥的顶点与底面圆周上任意一点的连线.如图中的PA,PB,PC.
2.圆锥的高:圆锥的顶点与底面圆心之间的线段.如图中的PO.
新课学习
四、圆锥及其相关概念
O
P
A
B
C
3.圆锥的母线、高、底面半径构成直角三角形.如图中的△AOP,△BOP.
新课学习
四、圆锥及其相关概念
4.圆锥的侧面展开图.如图将圆锥的侧面沿母线PA展开成一个扇形.即扇形PAB是图中圆锥的侧面展开图.
A
O
P
B
圆锥的母线
圆锥的底面周长
扇形的半径
扇形的弧长
结论
典例精析
例2.如图,如果从半径为9cm的圆形纸片剪去
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为_____.
剪去
典例精析
剪去
分析:要想求出圆锥的高,需知道圆锥的母线及底面半径,从已知中可得母线为9cm.
问题转化为:求底面半径.
典例精析
剪去
设底面半径为r,2πr=12π.解得r=6.
P
A
O
巩固练习
2.圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为_______.
1.已知圆锥的底面半径为5cm,
母线长为13cm,则这个圆锥的侧面积为____.
课堂小结
1.弧长公式:
3.圆锥侧面积:
2.扇形面积:
或
同学们再见
28.5
弧长和扇形面积的计算
第二十八章
圆
冀教版九上
学
习
目
标
1.探究弧长、扇形面积的计算公式.
2.了解圆锥的相关概念,知道圆锥的侧
面与扇形的关系.
3.能灵活运用弧长、扇形面积的计算
公式进行计算.
创设情境,引入新课
在圆中,圆心角与其所对的弧是一一对应的关系.即当圆心角确定时,其所对的弧也确定下来.
B
A
O
如图,⊙O中,当∠AOB确定下来时,其所对的AB确定下来,AB的长度也确定下来.
即∠AOB的大小影响AB的长度.
⌒
⌒
⌒
创设情境,引入新课
当圆心角被平均分成4份时,圆周也被平均分成4份,AC的长是⊙O周长的
⌒
D
B
C
A
O
弧与圆周的比等于圆心角与360°的比.
创设情境,引入新课
当圆心角被平均分成8份时,圆周也被平均分成8份,AE的长是⊙O周长的
⌒
B
A
C
D
O
●
E
F
M
N
弧与圆周的比等于圆心角与360°的比.
创设情境,引入新课
1°的圆心角所对的弧的长是⊙O周长的
A
O
●
P
创设情境,引入新课
10°的圆心角所对的弧长是圆周长的
类比:
32°的圆心角所对的弧长是圆周长的
117°的圆心角所对的弧长是圆周长的
200°的圆心角所对的弧长是圆周长的
n°的圆心角所对的弧长是圆周长的
新课学习
一、弧长公式
设圆的半径为r,n°的圆心角所对的弧的长为l.
影响弧长因素:
圆心角、半径
新课学习
解读公式:
公式中的变量有
,已知其中的
,可求出
l,n,r3个
2个
第3个.
如:
巩固练习
1.在半径为6cm的圆中,120°的圆心角所对的弧长为______.
4π
2.已知圆中一段弧的长为240π,半径为180,求这个弧所对的圆心角的度数.
新课学习
二、扇形
一条弧和经过这条弧端点的两条半径所组成的图形叫做扇形.
O
A
B
图中有两个扇形
O
A
B
O
A
B
扇形OAB
扇形OAB
巩固练习
1.判断下列图中红色线条围成的图形是不是扇形?
(1)
(2)
(3)
(4)
√
×
×
×
判断依据:一个端点在圆心,两个端点在圆上.
新课学习
三、扇形的面积
O
A
B
在圆中,与弧长类似,当圆心角确定时,与其对应的扇形也确定下来.
扇形面积与圆的面积之比等于圆心角与360°之比.
如:
圆心角为1°的扇形面积是圆面积的
圆心角为50°的扇形面积是圆面积的
圆心角为n°的扇形面积是圆面积的
新课学习
三、扇形的面积
设圆的半径为r,圆心角为n°的扇形的面积为S.
影响扇形面积的因素:
圆心角、半径
新课学习
解读公式:
公式中的变量有
,已知其中的
,可求出
S,n,r共3个
2个
第3个.
如:
新课学习
思考:
当圆心角确定下来时,其对应的弧及扇形都是唯一的,即两者也是一一对应的,它们的数量关系会是怎样的呢?
影响扇形面积的因素:
弧长、半径
新课学习
解读公式:
公式中的变量有
,已知其中的
,可求出
S,l,r共3个
2个
第3个.
如:
总结
扇形的面积公式:
或
根据题中给出的已知条件,选择合适的计算公式.
例1.已知扇形的圆心角为120°,弧长为2π,
求扇形的面积.
典例精析
分析:
问题转化为:已知圆心角为120°,弧长为2π,求半径.
例1.已知扇形的圆心角为120°,弧长为2π,
求扇形的面积.
典例精析
答:扇形的面积为3π.
巩固练习
1.一个扇形的圆心角为100°,面积为15π,
则此扇形的半径长为_____.
2.一个扇形的半径为6,圆心角为120°,
则此扇形的面积为_____.
3.扇形的弧长为20π,面积为240π,
则此扇形的半径为_____.
12π
24
新课学习
四、圆锥及其相关概念
O
P
A
B
C
1.圆锥的母线:圆锥的顶点与底面圆周上任意一点的连线.如图中的PA,PB,PC.
2.圆锥的高:圆锥的顶点与底面圆心之间的线段.如图中的PO.
新课学习
四、圆锥及其相关概念
O
P
A
B
C
3.圆锥的母线、高、底面半径构成直角三角形.如图中的△AOP,△BOP.
新课学习
四、圆锥及其相关概念
4.圆锥的侧面展开图.如图将圆锥的侧面沿母线PA展开成一个扇形.即扇形PAB是图中圆锥的侧面展开图.
A
O
P
B
圆锥的母线
圆锥的底面周长
扇形的半径
扇形的弧长
结论
典例精析
例2.如图,如果从半径为9cm的圆形纸片剪去
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为_____.
剪去
典例精析
剪去
分析:要想求出圆锥的高,需知道圆锥的母线及底面半径,从已知中可得母线为9cm.
问题转化为:求底面半径.
典例精析
剪去
设底面半径为r,2πr=12π.解得r=6.
P
A
O
巩固练习
2.圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为_______.
1.已知圆锥的底面半径为5cm,
母线长为13cm,则这个圆锥的侧面积为____.
课堂小结
1.弧长公式:
3.圆锥侧面积:
2.扇形面积:
或
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
