第24章一元二次方程复习与小结-冀教版九年级数学上册课件(23张)
文档属性
| 名称 | 第24章一元二次方程复习与小结-冀教版九年级数学上册课件(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 10:20:45 | ||
图片预览








文档简介
(共23张PPT)
复习与小结
冀教版九上
第二十四章
一元二次方程
学习目标
3.能选择合适的方法解方程,能熟练用一元二次方程解决应用题.
2.灵活运用根的判别式、根与系数的关系解决问题.
1.将本章知识点系统化.
冀教版九上
知识回顾
一、一元二次方程的概念及一般形式
概念:一元、二次、整式.
一般形式:
注意:1.概念中的三个条件缺一不可.
2.“系数”与“项”的区别.如二次项是
,而二次项系数是“a”.
知识运用
1.判断下列方程是否一元二次方程
2.指出下列方程中的a,b,c.
a=100,b=-10,c=-1
容易忽略化为一般形式后,二次项不存在
容易忽略限制条件“a≠0”
×
×
×
化为一般形式后,才能确定a,b,c.
盘点在运用“概念”及“一般形式”时你所掉过“坑”
知识回顾
二、解一元二次方程
1.直接开平方法;
2.配方法;
3.公式法;
4.因式分解法.(十字相乘法)
思想:
方法:
通过降次,将二次方程化为一次方程
知识运用
配方法
公式法
直接开平方法
因式分解法
十字相乘法
(a为1,b为偶数)
(其他方法都不合适时)
(左平方,右非负)
(可提公因式或用平方差分解因式)
(数较小时,可尝试)
注意:只有配方法、公式法可用于所有方程.
请为下列方程选择合适的解法
知识回顾
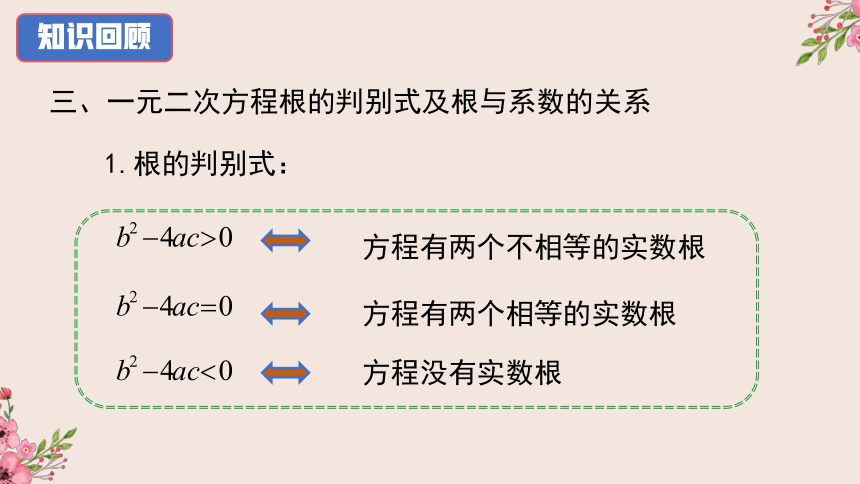
三、一元二次方程根的判别式及根与系数的关系
1.根的判别式:
方程有两个不相等的实数根
方程有两个相等的实数根
方程没有实数根
知识回顾
三、一元二次方程根的判别式及根与系数的关系
2.根与系数的关系:
如果一元二次方程
的两根分别为
那么
知识运用
盘点运用“根的判别式”及“根与系数的关系”时你所掉过的坑.
-3
知识运用
“根与系数关系”常见的题型.
-3
1
1.5
知识回顾
四、一元二次方程的应用
1.面积问题
2.两次增长率问题
3.握手问题
4.销售问题
5.其他问题
图形的面积公式
两次增长后=基数×(1+第一次增长率)×(1+第二次增长率)
(售价-进价)×数量=总利润
确定数量关系
知识运用
完成下列问题,只列方程
1.
如图,在宽为20m、长为32m的矩形地面上修建同样宽的小路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540㎡求小路的宽.设小路的宽为xm.
或
知识运用
完成下列问题,只列方程
2.九年级(3)班学生毕业时,每个同学都给其他同学写一份毕业留念作为纪念,全班学生共写了930份留言.设全班有x名学生.
3.若AB上共有45条线段(包含AB),求线段AB上共有多少个端点?设线段AB上有x个端点.
知识运用
完成下列问题,只列方程
4.已知某工厂把某种产品的年产量从2016年的100万台提高到2018年的121万台,求平均每年的增长率.设平均每年的增长率为x.
5.某公司一月份营业额为10万元,第一季度总营业额为33.1万元,该公司二、三月份营业额的平均增长率为x.
知识运用
完成下列问题,只列方程
6.某商品的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,商家想获得6080元的利润,应将销售单价定为多少元?
设销售单价为每件x元.
设销售单价为每件降了x元.
或
典例精析
例1.
(1)求证:方程有两个不相等的实数根.
∴方程有两个不相等的实数根.
“-”不可省略
典例精析
例1.
(2)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.
要分类讨论
解:分两种情况:
①当BC为底边时.AB=AC.
即方程有两个相等的实数根.
由(1)得,方程有两个不相等的实数根.
∴这种情况不成立.
典例精析
例1.
(2)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.
当k+1做底边时,k=BC=5.此时三边为5,5,6.
当k做底边时,k+1=BC=5.解得k=4.此时三边为5,5,4.
综上,k的值为4或5.
②以BC为腰时,底边是AB或AC.
典例精析
例1.
(3)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当k取何值时,△ABC是以BC为斜边的直角三角形.
∴当k=3时,△ABC是以BC为斜边的
直角三角形.
典例精析
例2.在△ABC中,∠B=90°,点P从点A开始,沿AB边以1cm/s的速度向点B移动;点Q从点B开始,沿BC边以2cm/s的速度向点C移动.如果P、Q分别从A、B两点同时出发,几秒后△PBQ的面积等于8c㎡?
B
Q
P
C
A
设运动时间为xs
点P的运动路程为:AP=x
点Q的运动路程为:BQ=2x
分析:要关注动点的运动方向、时间、所走过的路程.
典例精析
例2.在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边以1cm/s的速度向点B移动;点Q从点B开始,沿BC边以2cm/s的速度向点C移动.如果P、Q分别从A、B两点同时出发,几秒后△PBQ的面积等于8c㎡?
B
Q
P
C
A
解:设xs后△PBQ的面积等于8.由题意得
x
2x
6-x
∴2s或4s后△PBQ的面积等于8.
△PBQ的面积能等于20c㎡吗?
分析:
∴△PBQ的面积不能等于20c㎡.
“能不能”
方程“有没有”根
巩固提升
避坑宝典
1.隐含条件:a≠0.
3.选择合适方法解方程,减小计算量,提高准确率.
4.结果要符合实际意义.
5.“能不能”转化为方程“有没有”根的问题.
同学们再见
复习与小结
冀教版九上
第二十四章
一元二次方程
学习目标
3.能选择合适的方法解方程,能熟练用一元二次方程解决应用题.
2.灵活运用根的判别式、根与系数的关系解决问题.
1.将本章知识点系统化.
冀教版九上
知识回顾
一、一元二次方程的概念及一般形式
概念:一元、二次、整式.
一般形式:
注意:1.概念中的三个条件缺一不可.
2.“系数”与“项”的区别.如二次项是
,而二次项系数是“a”.
知识运用
1.判断下列方程是否一元二次方程
2.指出下列方程中的a,b,c.
a=100,b=-10,c=-1
容易忽略化为一般形式后,二次项不存在
容易忽略限制条件“a≠0”
×
×
×
化为一般形式后,才能确定a,b,c.
盘点在运用“概念”及“一般形式”时你所掉过“坑”
知识回顾
二、解一元二次方程
1.直接开平方法;
2.配方法;
3.公式法;
4.因式分解法.(十字相乘法)
思想:
方法:
通过降次,将二次方程化为一次方程
知识运用
配方法
公式法
直接开平方法
因式分解法
十字相乘法
(a为1,b为偶数)
(其他方法都不合适时)
(左平方,右非负)
(可提公因式或用平方差分解因式)
(数较小时,可尝试)
注意:只有配方法、公式法可用于所有方程.
请为下列方程选择合适的解法
知识回顾
三、一元二次方程根的判别式及根与系数的关系
1.根的判别式:
方程有两个不相等的实数根
方程有两个相等的实数根
方程没有实数根
知识回顾
三、一元二次方程根的判别式及根与系数的关系
2.根与系数的关系:
如果一元二次方程
的两根分别为
那么
知识运用
盘点运用“根的判别式”及“根与系数的关系”时你所掉过的坑.
-3
知识运用
“根与系数关系”常见的题型.
-3
1
1.5
知识回顾
四、一元二次方程的应用
1.面积问题
2.两次增长率问题
3.握手问题
4.销售问题
5.其他问题
图形的面积公式
两次增长后=基数×(1+第一次增长率)×(1+第二次增长率)
(售价-进价)×数量=总利润
确定数量关系
知识运用
完成下列问题,只列方程
1.
如图,在宽为20m、长为32m的矩形地面上修建同样宽的小路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540㎡求小路的宽.设小路的宽为xm.
或
知识运用
完成下列问题,只列方程
2.九年级(3)班学生毕业时,每个同学都给其他同学写一份毕业留念作为纪念,全班学生共写了930份留言.设全班有x名学生.
3.若AB上共有45条线段(包含AB),求线段AB上共有多少个端点?设线段AB上有x个端点.
知识运用
完成下列问题,只列方程
4.已知某工厂把某种产品的年产量从2016年的100万台提高到2018年的121万台,求平均每年的增长率.设平均每年的增长率为x.
5.某公司一月份营业额为10万元,第一季度总营业额为33.1万元,该公司二、三月份营业额的平均增长率为x.
知识运用
完成下列问题,只列方程
6.某商品的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,商家想获得6080元的利润,应将销售单价定为多少元?
设销售单价为每件x元.
设销售单价为每件降了x元.
或
典例精析
例1.
(1)求证:方程有两个不相等的实数根.
∴方程有两个不相等的实数根.
“-”不可省略
典例精析
例1.
(2)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.
要分类讨论
解:分两种情况:
①当BC为底边时.AB=AC.
即方程有两个相等的实数根.
由(1)得,方程有两个不相等的实数根.
∴这种情况不成立.
典例精析
例1.
(2)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.
当k+1做底边时,k=BC=5.此时三边为5,5,6.
当k做底边时,k+1=BC=5.解得k=4.此时三边为5,5,4.
综上,k的值为4或5.
②以BC为腰时,底边是AB或AC.
典例精析
例1.
(3)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当k取何值时,△ABC是以BC为斜边的直角三角形.
∴当k=3时,△ABC是以BC为斜边的
直角三角形.
典例精析
例2.在△ABC中,∠B=90°,点P从点A开始,沿AB边以1cm/s的速度向点B移动;点Q从点B开始,沿BC边以2cm/s的速度向点C移动.如果P、Q分别从A、B两点同时出发,几秒后△PBQ的面积等于8c㎡?
B
Q
P
C
A
设运动时间为xs
点P的运动路程为:AP=x
点Q的运动路程为:BQ=2x
分析:要关注动点的运动方向、时间、所走过的路程.
典例精析
例2.在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边以1cm/s的速度向点B移动;点Q从点B开始,沿BC边以2cm/s的速度向点C移动.如果P、Q分别从A、B两点同时出发,几秒后△PBQ的面积等于8c㎡?
B
Q
P
C
A
解:设xs后△PBQ的面积等于8.由题意得
x
2x
6-x
∴2s或4s后△PBQ的面积等于8.
△PBQ的面积能等于20c㎡吗?
分析:
∴△PBQ的面积不能等于20c㎡.
“能不能”
方程“有没有”根
巩固提升
避坑宝典
1.隐含条件:a≠0.
3.选择合适方法解方程,减小计算量,提高准确率.
4.结果要符合实际意义.
5.“能不能”转化为方程“有没有”根的问题.
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
