京改版九年级上册 数学 课件: 19.6 反比例函数的图象、性质、应用(24张PPT)
文档属性
| 名称 | 京改版九年级上册 数学 课件: 19.6 反比例函数的图象、性质、应用(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 749.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 10:22:23 | ||
图片预览







文档简介
(共24张PPT)
19.6
反比例函数的图象、性质、应用
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是给人们带来光明
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
——老师与同学们共勉
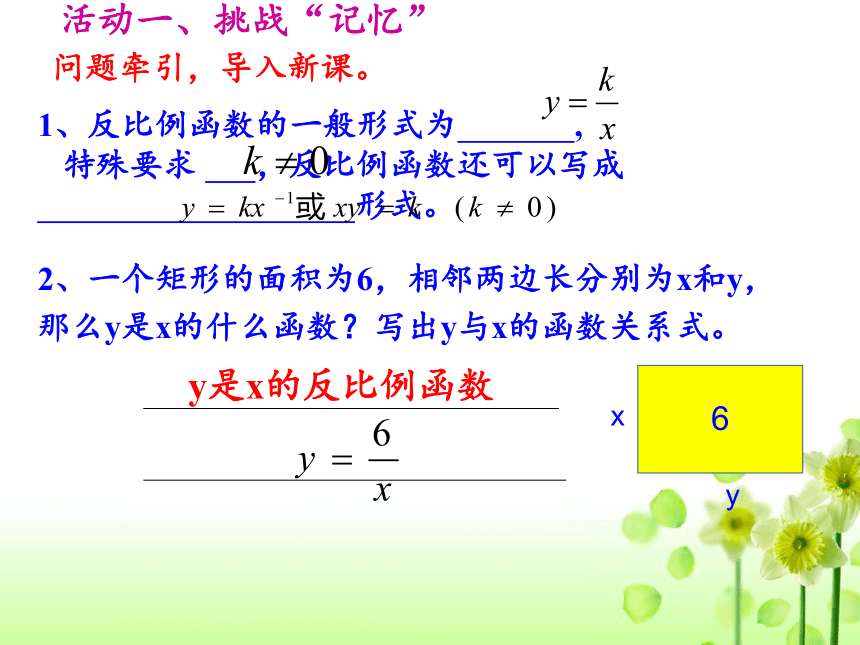
问题牵引,导入新课。
1、反比例函数的一般形式为
,
特殊要求
,反比例函数还可以写成
形式。
2、一个矩形的面积为6,相邻两边长分别为x和y,
那么y是x的什么函数?写出y与x的函数关系式。
y是x的反比例函数
x
y
6
活动一、挑战“记忆”
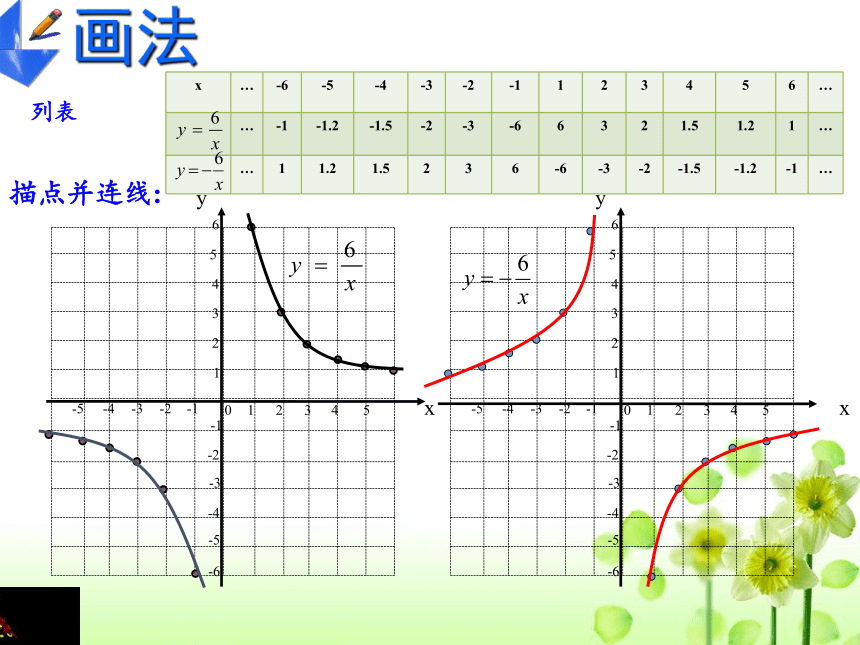
1、画反比例函数
与
的图象。
x
…
…
…
…
…
…
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
函数图象画法:描点法
1、列表;
2、描点;
3、连线。
心动不如行动
活动二、合作、探究、交流、展示
描点并连线:
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
…
…
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
…
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
画法
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
列表
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
活动三、观察发现规律,对比生成总结
看一看
想一想
议一议
议一议
看我的
反比例函数的基本性质
活动四、知识提炼
反比例函数(为常数,)图像是_____________.
当
k
>0
当k
<0
图像
性质
所在象限
增减性
对称性
远近性
双曲线两支
分别在第一、第三象限
双曲线两支
分别在第二、
第四象限
在每个象限内
y随x的增大
而减小;
在每个象限内
y随x的增大
而增大
双曲线
既关于坐标轴成轴对称,又关于原点成中心对称
越大,
图像离坐
标轴越远,
越小,
图像离坐
标轴越近,
但不会与坐
标轴相交.
活动五、用规律,练一练
1.请指出下面的图象中,哪一个是反比例函数
的图象
(
)
2.如图,是下列四个函数中哪一个函数的图象
(
)
B
C
D
A
C
C
3.
试分别说明反比例函数的图象所在的象限
.
4.若反比例函数
的图象在第二、第四象限,
则直线y=kx-3不经过第
象限。
5.
反比例函数y
=
的图象分布在二、四象限,
则k的取值范围是
.
一
(a≠0)
活动六、当堂检测
6
-3
k<4
k>4
D
已知点A(-3,a),B(-2,b),C(4,
c)在反比例函数
的图像上,比较a,b,c的大小.
活动七、拓展训练
能力提升
b<a<c
1.
(2017.广东)
在同一平面直角坐标系中,直线
y=k1x(k1≠0)与双曲线
(
k2≠0)相交于A、B两点,已知点A的坐标为(1,2),则点B的坐标为(
)
A.(-1,-2)
B.(-2,-1)
C.(-1,-1)
D.(-2,-2)
A
B
O
Y
X
驶向胜利的彼岸
A
活动八、
y
x
O
A.
y
x
O
B.
y
x
O
C.
y
x
O
D.
2.
(2008.江西)若点
在函数
(x<0)的图象上,且
,则它的图象大致是(
)
直击中考
活动八、
3.(2017.天津)若点A(-1,y1),B(1,y2),
C(3,y3)在反比例函数
的图像上,则y1,
y2,
y3的大小关系是(
)
A.y1<
y2<
y3
D.
y2
<
y1
<
y3
C.
y3
<
y2
<
y1
B.
y2<y3
<y1
B
B
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
反思
一个矩形的面积为6,相邻两边长分别为x和y,
那么y是x的什么函数?写出y与x的函数关系式,并画出图像。
x
y
6
(1)反比例函数 的图象由两条曲线组成,叫做双曲线。
(2)反比例函数 的图象,当k>0时,两支曲线分别位于
一、三象限内,当k<0
时,两支曲线分别位于第二、四象限内。
(3)因k≠0,x≠0故y≠0,所以它们都不与坐标轴相交。
(4)画图时注意其美观性(对称性、延伸性):反比例函数的图象既是中心对称图形,又是轴对称图形。它们各自都有一个对称中心两条对称轴;图象分别都是由两支曲线组成的,两个分支都无限趋近但永远不能与x轴和y轴相交。
本节课你收获了……
小结
布置作业:
1.导学案的思考题
2.书本P6的第2题,P8第3题
3.预习下一节课内容
驶向胜利的彼岸
感谢大家的参与
再
见
如图,在平面直角坐标系xoy中,双曲线
与直线
交于点A(-1,a)
(1)求a,m的值。
(2)求该双曲线与直线
另一个交点B的坐标。
A
B
O
y
x
Why?
课后思考?
教学预设:
通过这节课的学习,大部分学生会画反比例函数的图象,初步具备了用反比例函数的性质来解题的意识。但在教学过程中,有几点学生容易出现问题,一是连线时,反比例函数的图象是两支曲线,是不封闭的,有些学生容易画成封闭的;二时说明反比例函数
的图象所在的象限时,需要老师加以指导。教学中应体现学生的主体地位,教师只能起引导作用。
设计思路?
函数是在探索具体问题中数量关系和变化规律的基础上抽象出的重要数学概念,是研究现实世界变化规律的重要模型和方法。反比例函数也是日常生活和社会生产活动中较为常见的一个函数模型。学生曾在七年级下学期和八年级上学期学习过“变量之间的关系”和“一次函数”等内容,已经对函数有了初步的认识,在此基础上讨论反比例函数及其性质可以进一步领悟函数的概念并积累研究函数性质的方法及用函数观点处理实际问题的经验,为后继学习(如二次函数等)产生积极影响。
在总体设计思路上,本章与前面的有关函数类似,遵循了“问题情境--建立模型--拓展、应用”的模式,首先通过具体问题情境,让学生从实际问题情境中抽象出反比例函数的概念,以学生为主体,教师为引导,探索出反比例函数及其图象的主要性质,最后利用反比例函数图象及其性质解决有关现实问题。使知识得到升华,学以致用。
反比例函数
上一点P(x0,y0),过点P作PA⊥y轴,PB⊥X轴,垂足分别为A、B,则四边形AOBP的面积为
;且S△AOP
S△BOP
。
S△POD
= OD·PD
=
P
D
o
y
x
=
K的几何意义
理一理
函数
反比例函数
表达式
图象
及象限
形状
反比例函数的图象是_____________
位置
图象的两个分支分别位于
第_______
象限
图象的两个分支分别位于
第_______象限
性质
在每一个象限内:
当x>0时,y随x的增大而____;
当x<0时,y随x的增大而____.
k<0
y
x
0
y
0
k>0
x
在每一个象限内:
当x>0时,y随x的增大而____;
当x<0时,y随的增大而____.
反比例函数图象与性质
双曲线
知识点二
一、三
二、四
减小
减小
增大
增大
一、回顾交流、问题牵引
1、正比例函数y=kx(k是常数,k≠0),
一次函数y=kx+b(k是常数,k≠0)
2、二次函数
(a、b、c是常数,
a
≠0)
活动一、挑战“记忆”
谢
谢
19.6
反比例函数的图象、性质、应用
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是给人们带来光明
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
——老师与同学们共勉
问题牵引,导入新课。
1、反比例函数的一般形式为
,
特殊要求
,反比例函数还可以写成
形式。
2、一个矩形的面积为6,相邻两边长分别为x和y,
那么y是x的什么函数?写出y与x的函数关系式。
y是x的反比例函数
x
y
6
活动一、挑战“记忆”
1、画反比例函数
与
的图象。
x
…
…
…
…
…
…
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
函数图象画法:描点法
1、列表;
2、描点;
3、连线。
心动不如行动
活动二、合作、探究、交流、展示
描点并连线:
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
…
…
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
…
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
画法
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
列表
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
活动三、观察发现规律,对比生成总结
看一看
想一想
议一议
议一议
看我的
反比例函数的基本性质
活动四、知识提炼
反比例函数(为常数,)图像是_____________.
当
k
>0
当k
<0
图像
性质
所在象限
增减性
对称性
远近性
双曲线两支
分别在第一、第三象限
双曲线两支
分别在第二、
第四象限
在每个象限内
y随x的增大
而减小;
在每个象限内
y随x的增大
而增大
双曲线
既关于坐标轴成轴对称,又关于原点成中心对称
越大,
图像离坐
标轴越远,
越小,
图像离坐
标轴越近,
但不会与坐
标轴相交.
活动五、用规律,练一练
1.请指出下面的图象中,哪一个是反比例函数
的图象
(
)
2.如图,是下列四个函数中哪一个函数的图象
(
)
B
C
D
A
C
C
3.
试分别说明反比例函数的图象所在的象限
.
4.若反比例函数
的图象在第二、第四象限,
则直线y=kx-3不经过第
象限。
5.
反比例函数y
=
的图象分布在二、四象限,
则k的取值范围是
.
一
(a≠0)
活动六、当堂检测
6
-3
k<4
k>4
D
已知点A(-3,a),B(-2,b),C(4,
c)在反比例函数
的图像上,比较a,b,c的大小.
活动七、拓展训练
能力提升
b<a<c
1.
(2017.广东)
在同一平面直角坐标系中,直线
y=k1x(k1≠0)与双曲线
(
k2≠0)相交于A、B两点,已知点A的坐标为(1,2),则点B的坐标为(
)
A.(-1,-2)
B.(-2,-1)
C.(-1,-1)
D.(-2,-2)
A
B
O
Y
X
驶向胜利的彼岸
A
活动八、
y
x
O
A.
y
x
O
B.
y
x
O
C.
y
x
O
D.
2.
(2008.江西)若点
在函数
(x<0)的图象上,且
,则它的图象大致是(
)
直击中考
活动八、
3.(2017.天津)若点A(-1,y1),B(1,y2),
C(3,y3)在反比例函数
的图像上,则y1,
y2,
y3的大小关系是(
)
A.y1<
y2<
y3
D.
y2
<
y1
<
y3
C.
y3
<
y2
<
y1
B.
y2<y3
<y1
B
B
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
反思
一个矩形的面积为6,相邻两边长分别为x和y,
那么y是x的什么函数?写出y与x的函数关系式,并画出图像。
x
y
6
(1)反比例函数 的图象由两条曲线组成,叫做双曲线。
(2)反比例函数 的图象,当k>0时,两支曲线分别位于
一、三象限内,当k<0
时,两支曲线分别位于第二、四象限内。
(3)因k≠0,x≠0故y≠0,所以它们都不与坐标轴相交。
(4)画图时注意其美观性(对称性、延伸性):反比例函数的图象既是中心对称图形,又是轴对称图形。它们各自都有一个对称中心两条对称轴;图象分别都是由两支曲线组成的,两个分支都无限趋近但永远不能与x轴和y轴相交。
本节课你收获了……
小结
布置作业:
1.导学案的思考题
2.书本P6的第2题,P8第3题
3.预习下一节课内容
驶向胜利的彼岸
感谢大家的参与
再
见
如图,在平面直角坐标系xoy中,双曲线
与直线
交于点A(-1,a)
(1)求a,m的值。
(2)求该双曲线与直线
另一个交点B的坐标。
A
B
O
y
x
Why?
课后思考?
教学预设:
通过这节课的学习,大部分学生会画反比例函数的图象,初步具备了用反比例函数的性质来解题的意识。但在教学过程中,有几点学生容易出现问题,一是连线时,反比例函数的图象是两支曲线,是不封闭的,有些学生容易画成封闭的;二时说明反比例函数
的图象所在的象限时,需要老师加以指导。教学中应体现学生的主体地位,教师只能起引导作用。
设计思路?
函数是在探索具体问题中数量关系和变化规律的基础上抽象出的重要数学概念,是研究现实世界变化规律的重要模型和方法。反比例函数也是日常生活和社会生产活动中较为常见的一个函数模型。学生曾在七年级下学期和八年级上学期学习过“变量之间的关系”和“一次函数”等内容,已经对函数有了初步的认识,在此基础上讨论反比例函数及其性质可以进一步领悟函数的概念并积累研究函数性质的方法及用函数观点处理实际问题的经验,为后继学习(如二次函数等)产生积极影响。
在总体设计思路上,本章与前面的有关函数类似,遵循了“问题情境--建立模型--拓展、应用”的模式,首先通过具体问题情境,让学生从实际问题情境中抽象出反比例函数的概念,以学生为主体,教师为引导,探索出反比例函数及其图象的主要性质,最后利用反比例函数图象及其性质解决有关现实问题。使知识得到升华,学以致用。
反比例函数
上一点P(x0,y0),过点P作PA⊥y轴,PB⊥X轴,垂足分别为A、B,则四边形AOBP的面积为
;且S△AOP
S△BOP
。
S△POD
= OD·PD
=
P
D
o
y
x
=
K的几何意义
理一理
函数
反比例函数
表达式
图象
及象限
形状
反比例函数的图象是_____________
位置
图象的两个分支分别位于
第_______
象限
图象的两个分支分别位于
第_______象限
性质
在每一个象限内:
当x>0时,y随x的增大而____;
当x<0时,y随x的增大而____.
k<0
y
x
0
y
0
k>0
x
在每一个象限内:
当x>0时,y随x的增大而____;
当x<0时,y随的增大而____.
反比例函数图象与性质
双曲线
知识点二
一、三
二、四
减小
减小
增大
增大
一、回顾交流、问题牵引
1、正比例函数y=kx(k是常数,k≠0),
一次函数y=kx+b(k是常数,k≠0)
2、二次函数
(a、b、c是常数,
a
≠0)
活动一、挑战“记忆”
谢
谢
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
