人教版九年级上册 22.1.3二次函数y=a(x-h)^2 k的图象和性质(1) 同步练习(word版含答案)
文档属性
| 名称 | 人教版九年级上册 22.1.3二次函数y=a(x-h)^2 k的图象和性质(1) 同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 206.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 23:46:07 | ||
图片预览

文档简介
22.1.3二次函数y=a(x-h)^2
k的图象和性质(1)
一,选择题
1.与抛物线顶点相同,形状也相同,而开口方向相反的抛物线所对应的函数是(
)
A.
B.
C.
D.
2.抛物线y=-6x2可以看作是由抛物线y=-6x2+5按下列何种变换得到(
)
A.向上平移5个单位
B.向下平移5个单位
C.向左平移5个单位
D.向右平移5个单位
3.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图像大致为
(
)
A.答案A
B.答案B
C.答案C
D.答案D
二,填空题
4.当m=______时,抛物线y=(m+1)x+9开口向下,对称轴是______,在对称轴左侧,
y随x的增大而______;在对称轴右侧,y随x的增大而______.
5.将抛物线y=x2的图象向上平移1个单位,则平移后的抛物线的解析式为
.
6.抛物线y=x2-1的顶点坐标是
.
7.抛物线与y轴的交点坐标是
.
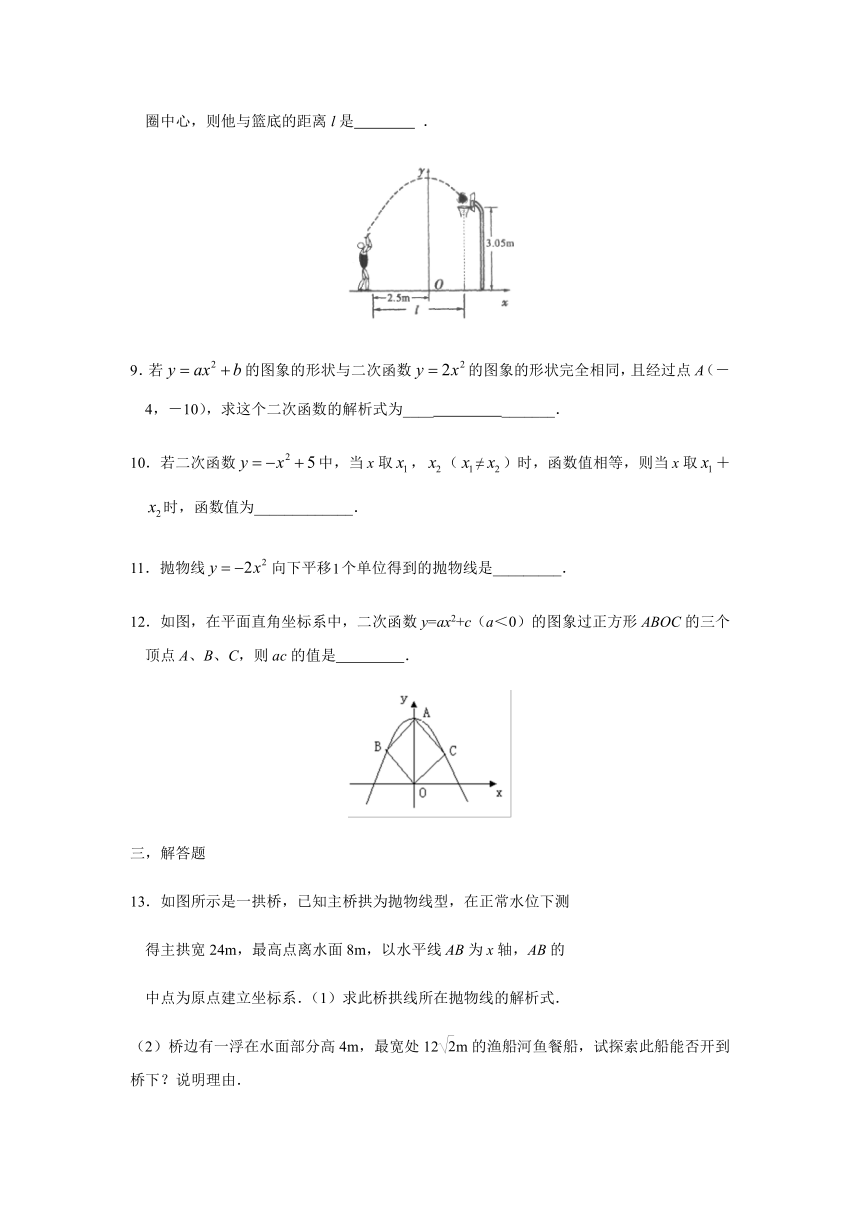
8.小敏在某次投篮中,球的运动路线是抛物线
的一部分(如图),若命中篮圈中心,则他与篮底的距离l是
.
9.若的图象的形状与二次函数的图象的形状完全相同,且经过点A(-4,-10),求这个二次函数的解析式为____
_______.
10.若二次函数中,当x取,(≠)时,函数值相等,则当x取+时,函数值为_____________.
11.抛物线向下平移个单位得到的抛物线是_________.
12.如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是
.
三,解答题
13.如图所示是一拱桥,已知主桥拱为抛物线型,在正常水位下测
得主拱宽24m,最高点离水面8m,以水平线AB为x轴,AB的
中点为原点建立坐标系.(1)求此桥拱线所在抛物线的解析式.
(2)桥边有一浮在水面部分高4m,最宽处12m的渔船河鱼餐船,试探索此船能否开到桥下?说明理由.
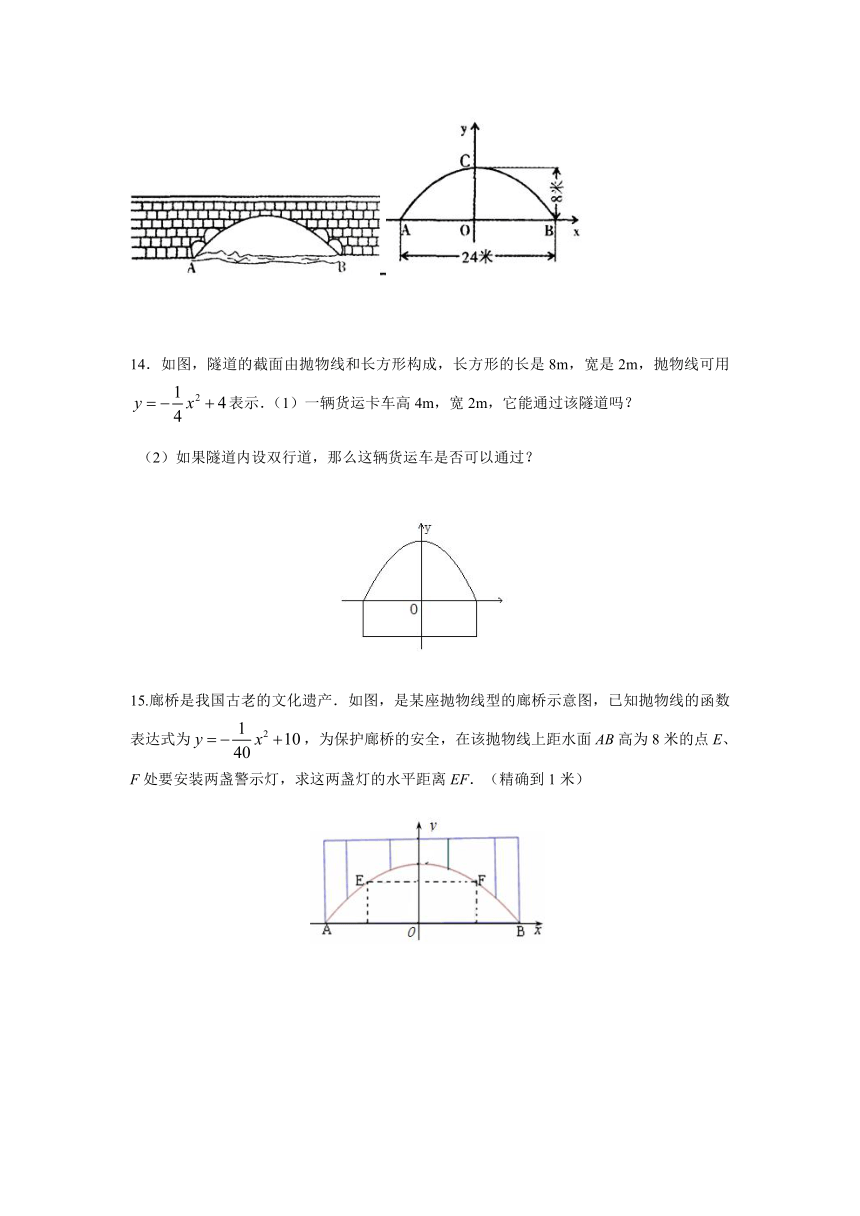
14.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可用表示.(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?
(2)如果隧道内设双行道,那么这辆货运车是否可以通过?
15.廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E、F处要安装两盏警示灯,求这两盏灯的水平距离EF.(精确到1米)
参考答案
一,选择题
1.
B.2.
B.3.B.
二,填空题
4.-2,
y轴,增大,减小.
5.
y=x2+1.
6.(0,-1).
7.(0,4).
8.
4.
9.
y=2x2-42,y=-2x2+20.
10.
5.
11.y=-2x2-1.
12.-2.
三,解答题
13.(1).设抛物线为
C点坐标代入得:c=8
,
A,B点坐标代入得:
,
解得,所求抛物线为;
(2)当y=4时得,,
高出水面4m处,拱宽(船宽),
所以此船在正常水位时不可以开到桥下.
14.(1)当x=±1时,y
=3.75,
3.75+2>4.
卡车可以通过.
(2)当x=±2时,y
=3,
3+2>4.
卡车可以通过.
15.由“在该抛物线上距水面AB高为8米的点”,
可知y=8,
把y=8代入y=-x2+10得:
x=±,
∴由两点间距离公式可求出EF=≈18(米).
k的图象和性质(1)
一,选择题
1.与抛物线顶点相同,形状也相同,而开口方向相反的抛物线所对应的函数是(
)
A.
B.
C.
D.
2.抛物线y=-6x2可以看作是由抛物线y=-6x2+5按下列何种变换得到(
)
A.向上平移5个单位
B.向下平移5个单位
C.向左平移5个单位
D.向右平移5个单位
3.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图像大致为
(
)
A.答案A
B.答案B
C.答案C
D.答案D
二,填空题
4.当m=______时,抛物线y=(m+1)x+9开口向下,对称轴是______,在对称轴左侧,
y随x的增大而______;在对称轴右侧,y随x的增大而______.
5.将抛物线y=x2的图象向上平移1个单位,则平移后的抛物线的解析式为
.
6.抛物线y=x2-1的顶点坐标是
.
7.抛物线与y轴的交点坐标是
.
8.小敏在某次投篮中,球的运动路线是抛物线
的一部分(如图),若命中篮圈中心,则他与篮底的距离l是
.
9.若的图象的形状与二次函数的图象的形状完全相同,且经过点A(-4,-10),求这个二次函数的解析式为____
_______.
10.若二次函数中,当x取,(≠)时,函数值相等,则当x取+时,函数值为_____________.
11.抛物线向下平移个单位得到的抛物线是_________.
12.如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是
.
三,解答题
13.如图所示是一拱桥,已知主桥拱为抛物线型,在正常水位下测
得主拱宽24m,最高点离水面8m,以水平线AB为x轴,AB的
中点为原点建立坐标系.(1)求此桥拱线所在抛物线的解析式.
(2)桥边有一浮在水面部分高4m,最宽处12m的渔船河鱼餐船,试探索此船能否开到桥下?说明理由.
14.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可用表示.(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?
(2)如果隧道内设双行道,那么这辆货运车是否可以通过?
15.廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E、F处要安装两盏警示灯,求这两盏灯的水平距离EF.(精确到1米)
参考答案
一,选择题
1.
B.2.
B.3.B.
二,填空题
4.-2,
y轴,增大,减小.
5.
y=x2+1.
6.(0,-1).
7.(0,4).
8.
4.
9.
y=2x2-42,y=-2x2+20.
10.
5.
11.y=-2x2-1.
12.-2.
三,解答题
13.(1).设抛物线为
C点坐标代入得:c=8
,
A,B点坐标代入得:
,
解得,所求抛物线为;
(2)当y=4时得,,
高出水面4m处,拱宽(船宽),
所以此船在正常水位时不可以开到桥下.
14.(1)当x=±1时,y
=3.75,
3.75+2>4.
卡车可以通过.
(2)当x=±2时,y
=3,
3+2>4.
卡车可以通过.
15.由“在该抛物线上距水面AB高为8米的点”,
可知y=8,
把y=8代入y=-x2+10得:
x=±,
∴由两点间距离公式可求出EF=≈18(米).
同课章节目录
