人教版七年级数学上册2.2整式的加减——合并同类项课件(25张ppt)
文档属性
| 名称 | 人教版七年级数学上册2.2整式的加减——合并同类项课件(25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 09:12:57 | ||
图片预览







文档简介
(共25张PPT)
2.2.1整式的加减
-------合并同类项
一、激发求知欲
1.整式的概念
2.单项式,单项式的系数,次数
3.多项式,多项式的项,多项式
的次数,
4、下列式子哪些是单项式?哪些是多项式?
,
,
,
5、求上题中多项式的项及各项的系数和次数.
解:多项式
的项是4ab、-4,其中4ab的系数是4、次数是2,-4的系数是-4、次数是0,
多项式
的项是a4、-2a2b2、b4,其中a4
的系数是1、次数是4,-2a2b2的系数是-2、次数是4,b4的系数是1、次数是4.
二、展示目标和任务
学习目标:
1、掌握同类项的概念,能识别同类项,学会合并同
类项并知道合并同类项所依据的运算律。
2、通过观察、思考、分析、归纳、小组合作,学会
了解数学的分类思想。
学习重难点:
1.同类项概念,以及合并同类项法则和基本步骤。
2.正确的判断同类项以及准确合并同类项。
对下类水果进行分类:
三、自主合作与交流
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(无论你用几个房间)
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
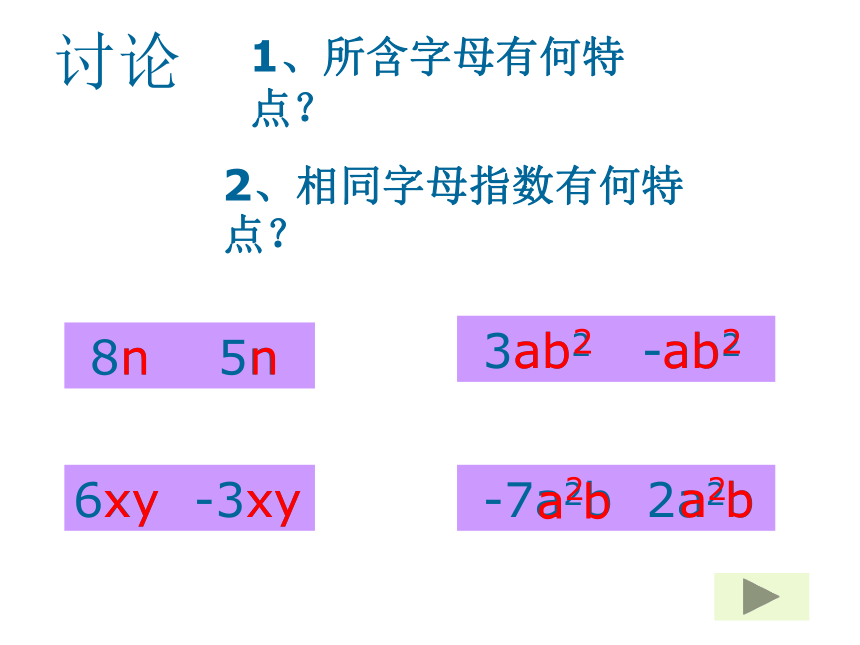
8n
5n
3ab2
-ab2
6xy
-3xy
-7a2b
2a2b
n
n
xy
xy
a
b
a
b
ab
ab
2
2
2
2
1、所含字母有何特
点?
2、相同字母指数有何特点?
讨论
探究新知:
1、同类项的概念:
概念:所含字母相同,并且相同字母的指数也相同的项,叫做同类项。
注意:
(1)
同类项与系数无关,
与字母的排列顺序也无关
(2)几个常数项也是同类项。
下列各组中的两项是不是同类项?
抢答
4
+
=
6
―
=
3
4a
2a
6
4xy
―
xy=
3xy
a
a
a
(1)运用运算律计算:
;
(2)根据(1)中的方法完成下面的运算,并说说其中的道理:
.
探究A:
探究B
填空:
(1)
;
(2)
;
(3)
.
每式的两项为什么能运算成一项?
把多项式中的同类项合并成一项叫合并
同类项。
2.合并同类项的定义:
一.是“字母和字母的指数不变”(同类项)
二.是“系数相加”(合并)
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变。
3.合并同类项法则
合并同类项的
:
要点
试一试.
合并下列各式的同类项:
(1)3x3+x3;
(2)xy2-
xy2。
解:(1)3x3+x3
=(3+1)x3
=4x3
(2)xy2-
xy2
=(1-
)xy2
=
xy2
=(
)+(
)
(1)
6xy-10x2-5yx+7x2
+5x
合并同类项
(找)
6xy-5yx
-10x2+7x2
(移)
=
xy
(6-5)
+
x2
(-10+7)
(并)
=xy-3x2
+5x
+5x
+5x
合作完成
因为多项式中的字母表示的是数,所以
我们也可以运用交换律、结合律、分配律把
多项式中的同类项进行合并。
1、所含的字母相同,并且相同字母的指数也相同的项叫做_______.
几个常数项也是______.
2、把多项式中的同类项合并成一项,叫做______________
.
3、合并同类项可简记为:系数
,字母
连同它的指数
.
4、通常我们把一个多项式的各项按照某个字母的指数从
(降幂)或者从____(升幂)的顺序排列.
同类项
同类项
合并同类项
相加
不变
大到小
小到大
四、成果展示,教师点拨
(2)
(3)
(4)
解:原式=
解:原式=
解:原式=(m+m)+(-n2-n2)
=(1+1)m+[(-1)+(-1)]n2
=2m-2n2
强化训练
五、知识验证提升
填空:
1.如果2a2bn+1与-4amb3是同类项,则
m=____,n=____;
2.若5xy2+axy2=-2xy2,则a=___;
3.在6xy-3x2-4x2y-5yx2+x2中没有同类项
的项是______;
2
2
-7
6xy
知
识
延
伸:
4.已知:
与
是同类项,
求
m、n的值
.
2
_
3
x3my3
-
1
_
4
x6yn+1
∴
3m=6
,
n+1=3
∴
m=2
,
n=2
解:
∵
与
是同类项
2
_
3
x3my3
-
1
_
4
x6yn+1
在合并同类项时结果往往是一个多项式,通常把这个结果写成按某一个字母的升幂或降幂的形式排列:
升幂排列:按照某字母的指数从小到大的
顺序排列
降幂排列:按照某字母的指数从大到小的
顺序排列
练习
1.把下列多项式按照升幂排列,然后再按照降幂排列
(1)
5a2+4-2a
(2)
x2-x4+2-5x
2.把多项式降幂排列
通过这节课的学习:
我学会了……
使我感触最深的是……
我发现生活中……
注意:
1.若两个同类项的系数互为相反数,则两项的和等于零,
如:-3ab2+3ab2=(-3+3)ab2=0×ab2=0。
2.多项式中只有同类项才能合并,不是同类项不能合并。
3.通常我们把一个多项式的各项按照某个字母的指数从
大到小(降幂)或者从小到大(升幂)的顺序排列,
如:-4x2+5x+5或写5+5x-4x2。
例1:合并下列各式的同类项:
(2)-3x2y+2x2y+3xy2-2xy2
解:
=(-3+2)x2y+(3-2)xy2
=-x2y+xy2
(3)4a2+3b2+2ab-4a2-4b2
=(4a2-4a2)+(3b2-4b2)+2ab
=(4-4)a2+(3-4)b2+2ab
=-b2+2ab
做一做:
解:(1)2x2-5x+x2+4x-3x2-2
=(2+1-3)x2+(-5+4)x-2
=-x-2
返回
下一张
上一张
退出
随堂练习:
1.下列各对不是同类项的是(
)
A
-3x2y与2x2y
B
-2xy2与
3x2y
C
-5x2y与3yx2
D
3mn2与2mn2
2.合并同类项正确的是(
)
A
4a+b=5ab
B
6xy2-6y2x=0
C
6x2-4x2=2
D
3x2+2x3=5x5
B
B
青春是有限的,智慧是无穷的,趁短的青春,去学习无穷的智慧。
————??高尔基
2.2.1整式的加减
-------合并同类项
一、激发求知欲
1.整式的概念
2.单项式,单项式的系数,次数
3.多项式,多项式的项,多项式
的次数,
4、下列式子哪些是单项式?哪些是多项式?
,
,
,
5、求上题中多项式的项及各项的系数和次数.
解:多项式
的项是4ab、-4,其中4ab的系数是4、次数是2,-4的系数是-4、次数是0,
多项式
的项是a4、-2a2b2、b4,其中a4
的系数是1、次数是4,-2a2b2的系数是-2、次数是4,b4的系数是1、次数是4.
二、展示目标和任务
学习目标:
1、掌握同类项的概念,能识别同类项,学会合并同
类项并知道合并同类项所依据的运算律。
2、通过观察、思考、分析、归纳、小组合作,学会
了解数学的分类思想。
学习重难点:
1.同类项概念,以及合并同类项法则和基本步骤。
2.正确的判断同类项以及准确合并同类项。
对下类水果进行分类:
三、自主合作与交流
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(无论你用几个房间)
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
8n
5n
3ab2
-ab2
6xy
-3xy
-7a2b
2a2b
n
n
xy
xy
a
b
a
b
ab
ab
2
2
2
2
1、所含字母有何特
点?
2、相同字母指数有何特点?
讨论
探究新知:
1、同类项的概念:
概念:所含字母相同,并且相同字母的指数也相同的项,叫做同类项。
注意:
(1)
同类项与系数无关,
与字母的排列顺序也无关
(2)几个常数项也是同类项。
下列各组中的两项是不是同类项?
抢答
4
+
=
6
―
=
3
4a
2a
6
4xy
―
xy=
3xy
a
a
a
(1)运用运算律计算:
;
(2)根据(1)中的方法完成下面的运算,并说说其中的道理:
.
探究A:
探究B
填空:
(1)
;
(2)
;
(3)
.
每式的两项为什么能运算成一项?
把多项式中的同类项合并成一项叫合并
同类项。
2.合并同类项的定义:
一.是“字母和字母的指数不变”(同类项)
二.是“系数相加”(合并)
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变。
3.合并同类项法则
合并同类项的
:
要点
试一试.
合并下列各式的同类项:
(1)3x3+x3;
(2)xy2-
xy2。
解:(1)3x3+x3
=(3+1)x3
=4x3
(2)xy2-
xy2
=(1-
)xy2
=
xy2
=(
)+(
)
(1)
6xy-10x2-5yx+7x2
+5x
合并同类项
(找)
6xy-5yx
-10x2+7x2
(移)
=
xy
(6-5)
+
x2
(-10+7)
(并)
=xy-3x2
+5x
+5x
+5x
合作完成
因为多项式中的字母表示的是数,所以
我们也可以运用交换律、结合律、分配律把
多项式中的同类项进行合并。
1、所含的字母相同,并且相同字母的指数也相同的项叫做_______.
几个常数项也是______.
2、把多项式中的同类项合并成一项,叫做______________
.
3、合并同类项可简记为:系数
,字母
连同它的指数
.
4、通常我们把一个多项式的各项按照某个字母的指数从
(降幂)或者从____(升幂)的顺序排列.
同类项
同类项
合并同类项
相加
不变
大到小
小到大
四、成果展示,教师点拨
(2)
(3)
(4)
解:原式=
解:原式=
解:原式=(m+m)+(-n2-n2)
=(1+1)m+[(-1)+(-1)]n2
=2m-2n2
强化训练
五、知识验证提升
填空:
1.如果2a2bn+1与-4amb3是同类项,则
m=____,n=____;
2.若5xy2+axy2=-2xy2,则a=___;
3.在6xy-3x2-4x2y-5yx2+x2中没有同类项
的项是______;
2
2
-7
6xy
知
识
延
伸:
4.已知:
与
是同类项,
求
m、n的值
.
2
_
3
x3my3
-
1
_
4
x6yn+1
∴
3m=6
,
n+1=3
∴
m=2
,
n=2
解:
∵
与
是同类项
2
_
3
x3my3
-
1
_
4
x6yn+1
在合并同类项时结果往往是一个多项式,通常把这个结果写成按某一个字母的升幂或降幂的形式排列:
升幂排列:按照某字母的指数从小到大的
顺序排列
降幂排列:按照某字母的指数从大到小的
顺序排列
练习
1.把下列多项式按照升幂排列,然后再按照降幂排列
(1)
5a2+4-2a
(2)
x2-x4+2-5x
2.把多项式降幂排列
通过这节课的学习:
我学会了……
使我感触最深的是……
我发现生活中……
注意:
1.若两个同类项的系数互为相反数,则两项的和等于零,
如:-3ab2+3ab2=(-3+3)ab2=0×ab2=0。
2.多项式中只有同类项才能合并,不是同类项不能合并。
3.通常我们把一个多项式的各项按照某个字母的指数从
大到小(降幂)或者从小到大(升幂)的顺序排列,
如:-4x2+5x+5或写5+5x-4x2。
例1:合并下列各式的同类项:
(2)-3x2y+2x2y+3xy2-2xy2
解:
=(-3+2)x2y+(3-2)xy2
=-x2y+xy2
(3)4a2+3b2+2ab-4a2-4b2
=(4a2-4a2)+(3b2-4b2)+2ab
=(4-4)a2+(3-4)b2+2ab
=-b2+2ab
做一做:
解:(1)2x2-5x+x2+4x-3x2-2
=(2+1-3)x2+(-5+4)x-2
=-x-2
返回
下一张
上一张
退出
随堂练习:
1.下列各对不是同类项的是(
)
A
-3x2y与2x2y
B
-2xy2与
3x2y
C
-5x2y与3yx2
D
3mn2与2mn2
2.合并同类项正确的是(
)
A
4a+b=5ab
B
6xy2-6y2x=0
C
6x2-4x2=2
D
3x2+2x3=5x5
B
B
青春是有限的,智慧是无穷的,趁短的青春,去学习无穷的智慧。
————??高尔基
