2020年秋人教版八年级数学上册随课练——12.3角的平分线的性质学情练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版八年级数学上册随课练——12.3角的平分线的性质学情练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 145.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 14:02:34 | ||
图片预览


文档简介
12.3角的平分线的性质学情练习
一、选择题
1.如图,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是(
)
A.BD+ED=BC
B.DE平分∠ADB
C.AD平分∠EDC
D.ED+AC>AD
2.已知Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD:CD=9:7,则D到AB边的距离为(
)
A.18
B.16
C.14
D.12
3.如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为(??
)
A.?α??????????????????????????????
????B.???????????????????????????????????
C.?90﹣α??????????????????????????????????D.?90﹣
α
4.与相交的两直线距离相等的点是在(
)
A.一条射线上
B.一条直线上
C.两条互相垂直的直线上
D.以上都不对
5.给出下列结论,正确的有(
)
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个
B.2个
C.3个
D.4个
6.如图,已知△ABC中,∠C=90°,AD平分∠BAC,且CD:BD=3:4.若BC=21,则点D到AB边的距离为(???
)
A.?7?????????????????????????????????????????
?B.?9??????????????????????????????????????????
C.?11??????????????????????????????????????????D.?14
7.如图,△ABC中,∠C
=
90°,AC
=
BC,AD是∠BAC的平分线,DE⊥AB于E,若AC
=
10cm,则△DBE的周长等于(
)
A.10cm
B.8cm
C.6cm
D.9cm
8.如图,在边长为的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
A.
B.
C.
D.1
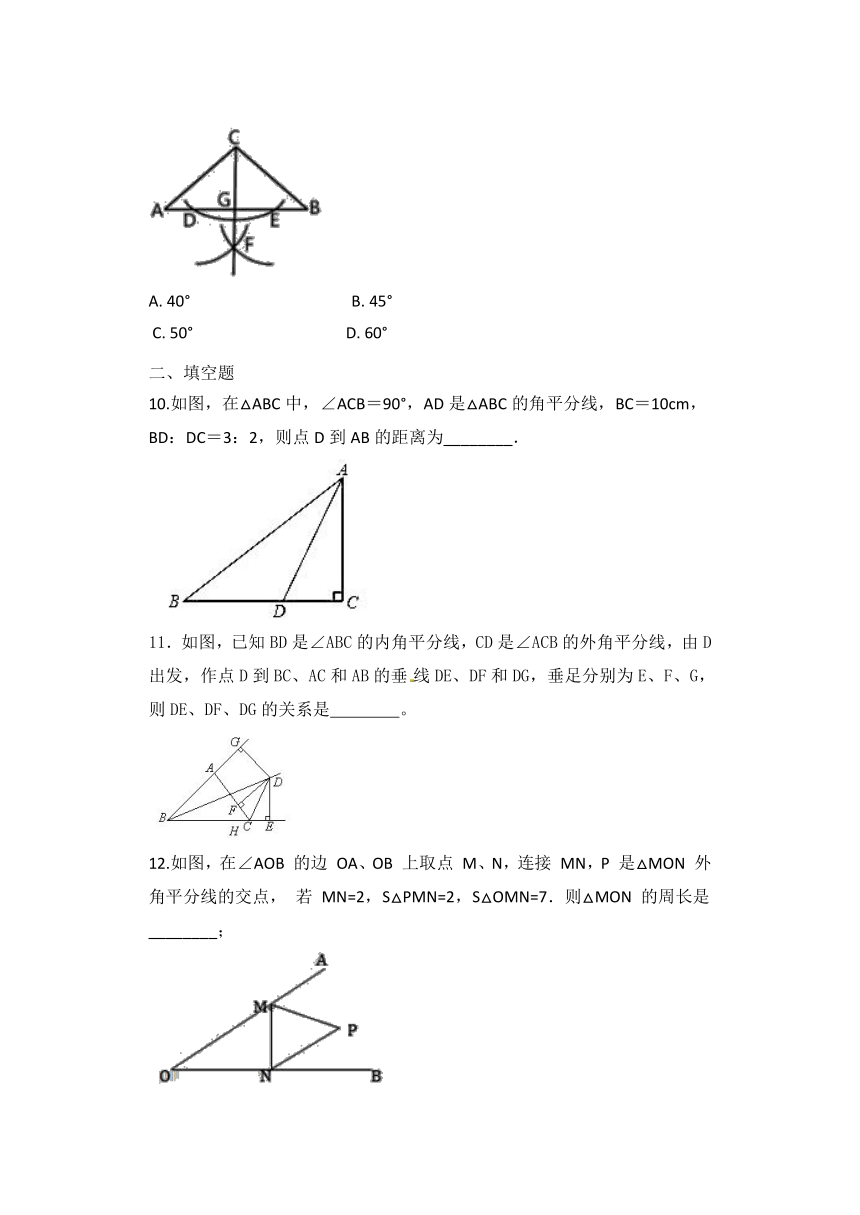
9.如图在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为(???
)
A.?40°????????????????????????????????????
???B.?45°??????????????????????????????????????
?C.?50°???????????????????????????????????????D.?60°
二、填空题
10.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为________.
11.如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是
。
12.如图,在∠AOB
的边
OA、OB
上取点
M、N,连接
MN,P
是△MON
外角平分线的交点,
若
MN=2,S△PMN=2,S△OMN=7.则△MON
的周长是________;
13.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于______.
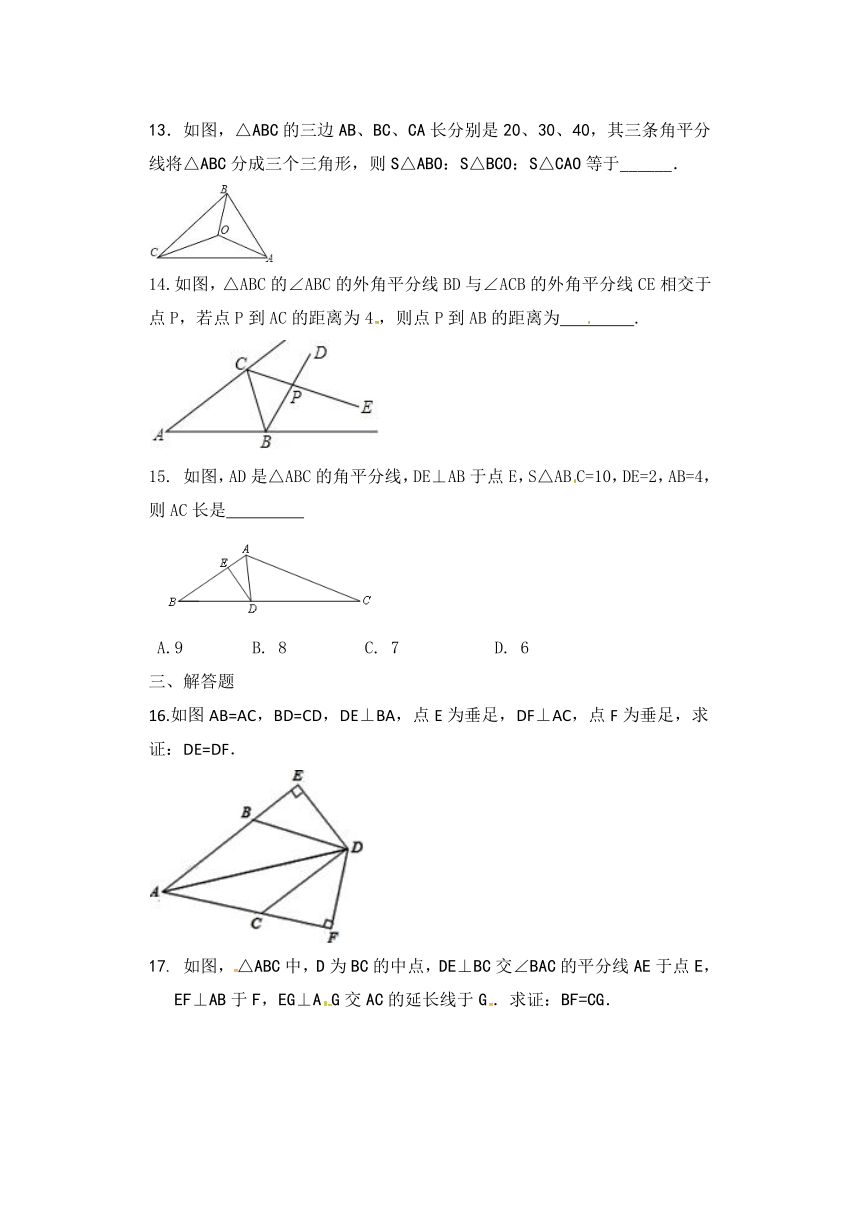
14.如图,△ABC的∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,若点P到AC的距离为4,则点P到AB的距离为
.
15.
如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=10,DE=2,AB=4,
则AC长是
A.9
B.
8
C.
7
D.
6
三、解答题
16.如图AB=AC,BD=CD,DE⊥BA,点E为垂足,DF⊥AC,点F为垂足,求证:DE=DF.
17.
如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E,EF⊥AB于F,EG⊥AG交AC的延长线于G.求证:BF=CG.
18.如图,△ABC的角平分线AD、BE相交于点P,
(1)在图1中,分别画出点P到边AC、BC、BA的垂线段PF、PG、PH,这三条线段相等吗?为什么?
(2)在图2中,∠ABC是直角,∠C=60°,其余条件都不变,请你判断并写出PE与PD之间的数量关系,并说明理由.
19.如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
20.
如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
答案
1.
C
2.
C
3.
C
4.
C
5.
B
6.
B
7.
B
8.
D
9.
C
10.
4
11.
DE=DF=DG
12.
11
13.
2:3:4.
14.
4
15.
D
16.
证明:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∵DE⊥BA,DF⊥AC,
∴DE=DF.
17.
证明:连接BE、EC,
∵ED⊥BC,
D为BC中点,
∴BE=EC,
∵EF⊥AB
EG⊥AG,
且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中
,
∴Rt△BFE≌Rt△CGE,
∴BF=CG
18.
(1)PF=PH=PG,理由如下:∵AD平分∠BAC,PF⊥AC,PH⊥AB,
∴PF=PH.
∵BE平分∠ABC,PG⊥BC,PH⊥AB,
∴PG=PH.∴PF=PH=PG.
(2)PE=PD.
理由如下:∵∠ABC=90°,∠C=60°,∴∠CAB=30°.
∵AD平分∠BAC,BE平分∠ABC,
∴∠CAD=∠BAD=∠CAB=15°,∠ABE=∠CBE=∠ABC=45°.
过点P作PF⊥AC,PG⊥BC,垂足分别为F、G,则∠PFE=∠PGD=90°.
∵∠PDG=∠C+∠CAD=60°+15°=75°,∠PEF=∠CAB+∠ABE=30°+45°=75°,
∴∠PEF=∠PDG.
∵PF⊥AC,PG⊥BC,
∴∠PFE=∠PGD=90°.
由(1)得PF=PG,
∴△PFE≌△PGD.∴PE=PD.
19.
解:如图
过点D作DF⊥BC于F,
∵BD是∠ABC的平分线,DE⊥AB,
∴DE=DF,
∴S△ABC=AB?DE+BC?DF=90,
即×18?DE+×12?DE=90,
解得DE=6.
20.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
一、选择题
1.如图,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是(
)
A.BD+ED=BC
B.DE平分∠ADB
C.AD平分∠EDC
D.ED+AC>AD
2.已知Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD:CD=9:7,则D到AB边的距离为(
)
A.18
B.16
C.14
D.12
3.如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为(??
)
A.?α??????????????????????????????
????B.???????????????????????????????????
C.?90﹣α??????????????????????????????????D.?90﹣
α
4.与相交的两直线距离相等的点是在(
)
A.一条射线上
B.一条直线上
C.两条互相垂直的直线上
D.以上都不对
5.给出下列结论,正确的有(
)
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个
B.2个
C.3个
D.4个
6.如图,已知△ABC中,∠C=90°,AD平分∠BAC,且CD:BD=3:4.若BC=21,则点D到AB边的距离为(???
)
A.?7?????????????????????????????????????????
?B.?9??????????????????????????????????????????
C.?11??????????????????????????????????????????D.?14
7.如图,△ABC中,∠C
=
90°,AC
=
BC,AD是∠BAC的平分线,DE⊥AB于E,若AC
=
10cm,则△DBE的周长等于(
)
A.10cm
B.8cm
C.6cm
D.9cm
8.如图,在边长为的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
A.
B.
C.
D.1
9.如图在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为(???
)
A.?40°????????????????????????????????????
???B.?45°??????????????????????????????????????
?C.?50°???????????????????????????????????????D.?60°
二、填空题
10.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为________.
11.如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是
。
12.如图,在∠AOB
的边
OA、OB
上取点
M、N,连接
MN,P
是△MON
外角平分线的交点,
若
MN=2,S△PMN=2,S△OMN=7.则△MON
的周长是________;
13.如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于______.
14.如图,△ABC的∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,若点P到AC的距离为4,则点P到AB的距离为
.
15.
如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=10,DE=2,AB=4,
则AC长是
A.9
B.
8
C.
7
D.
6
三、解答题
16.如图AB=AC,BD=CD,DE⊥BA,点E为垂足,DF⊥AC,点F为垂足,求证:DE=DF.
17.
如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E,EF⊥AB于F,EG⊥AG交AC的延长线于G.求证:BF=CG.
18.如图,△ABC的角平分线AD、BE相交于点P,
(1)在图1中,分别画出点P到边AC、BC、BA的垂线段PF、PG、PH,这三条线段相等吗?为什么?
(2)在图2中,∠ABC是直角,∠C=60°,其余条件都不变,请你判断并写出PE与PD之间的数量关系,并说明理由.
19.如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
20.
如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
答案
1.
C
2.
C
3.
C
4.
C
5.
B
6.
B
7.
B
8.
D
9.
C
10.
4
11.
DE=DF=DG
12.
11
13.
2:3:4.
14.
4
15.
D
16.
证明:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∵DE⊥BA,DF⊥AC,
∴DE=DF.
17.
证明:连接BE、EC,
∵ED⊥BC,
D为BC中点,
∴BE=EC,
∵EF⊥AB
EG⊥AG,
且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中
,
∴Rt△BFE≌Rt△CGE,
∴BF=CG
18.
(1)PF=PH=PG,理由如下:∵AD平分∠BAC,PF⊥AC,PH⊥AB,
∴PF=PH.
∵BE平分∠ABC,PG⊥BC,PH⊥AB,
∴PG=PH.∴PF=PH=PG.
(2)PE=PD.
理由如下:∵∠ABC=90°,∠C=60°,∴∠CAB=30°.
∵AD平分∠BAC,BE平分∠ABC,
∴∠CAD=∠BAD=∠CAB=15°,∠ABE=∠CBE=∠ABC=45°.
过点P作PF⊥AC,PG⊥BC,垂足分别为F、G,则∠PFE=∠PGD=90°.
∵∠PDG=∠C+∠CAD=60°+15°=75°,∠PEF=∠CAB+∠ABE=30°+45°=75°,
∴∠PEF=∠PDG.
∵PF⊥AC,PG⊥BC,
∴∠PFE=∠PGD=90°.
由(1)得PF=PG,
∴△PFE≌△PGD.∴PE=PD.
19.
解:如图
过点D作DF⊥BC于F,
∵BD是∠ABC的平分线,DE⊥AB,
∴DE=DF,
∴S△ABC=AB?DE+BC?DF=90,
即×18?DE+×12?DE=90,
解得DE=6.
20.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
