北师大版九年级数学下册第三章 圆 单元测试题(Word版 含解析)
文档属性
| 名称 | 北师大版九年级数学下册第三章 圆 单元测试题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 314.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-21 00:00:00 | ||
图片预览


文档简介
北师大版九年级数学下册第三章
圆
单元测试题
一.选择题
1.A、B、C分别表示三个村庄,AB=1700米,BC=800米,AC=1500米,某社区拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB的中点
B.BC的中点
C.AC的中点
D.∠C的平分线与AB的交点
2.如图,⊙O中,若OA⊥BC、∠AOB=66°,则∠ADC的度数为( )
A.33°
B.56°
C.57°
D.66°
3.如图,AB是直径,C、D为圆上的点,已知∠D为30°,则∠CAB的度数为( )
A.45°
B.50°
C.55°
D.60°
4.如图所示,四边形ABCD是圆O的内接四边形,∠A=45°,BC=4,CD=2,则弦BD的长为( )
A.2
B.3
C.
D.2
5.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则的长为( )
A.2π
B.4π
C.
D.π
6.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )
A.h=R+r
B.R=2r
C.r=a
D.R=a
7.如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125°
B.130°
C.135°
D.140°
8.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55°
B.65°
C.60°
D.75°
9.如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
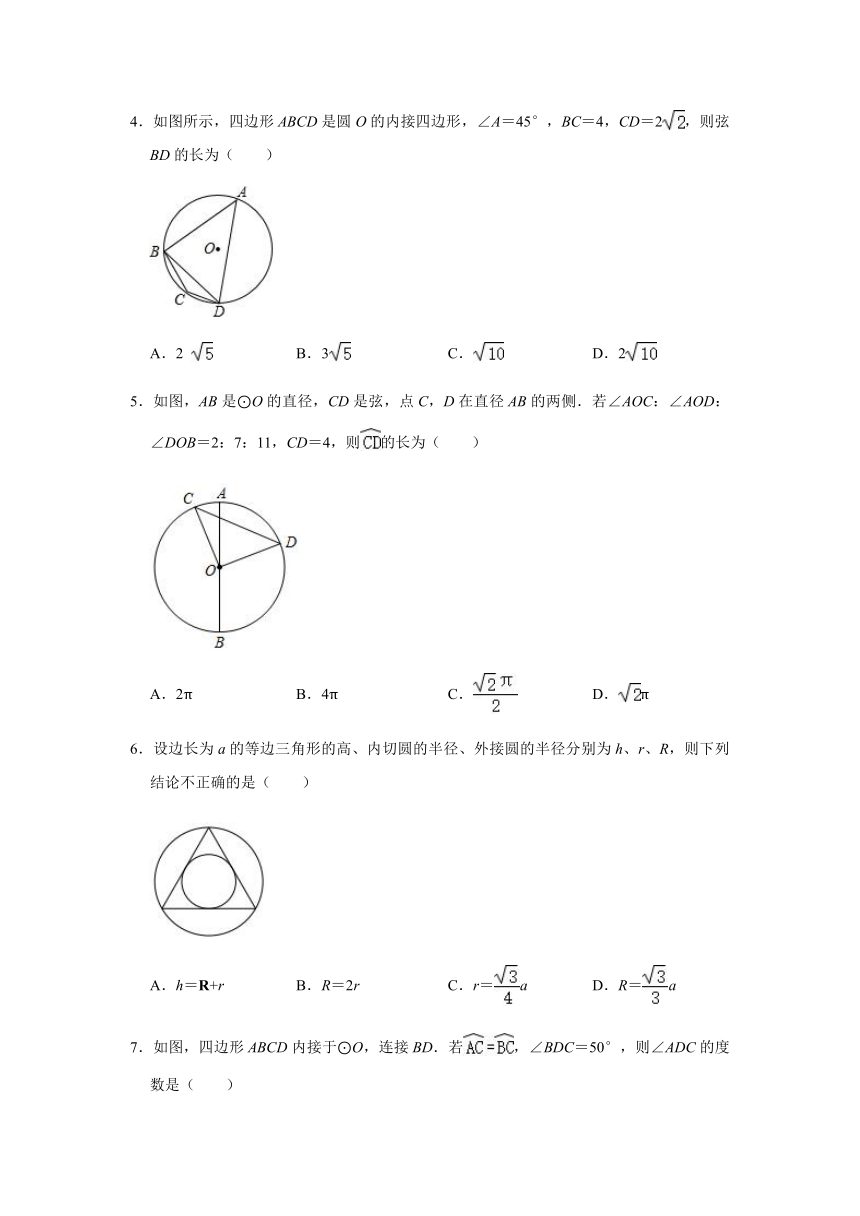
10.如图,已知⊙O的半径为10,A、B是⊙O上的两点,∠AOB=90°,C是射线OB上一个动点,连结AC并延长交⊙O于点D,过点D作DE⊥OD交OB的延长线于点E.当∠A从30°增大到60°时,弦AD在圆内扫过的面积是( )
A.
B.
C.
D.
二、填空题
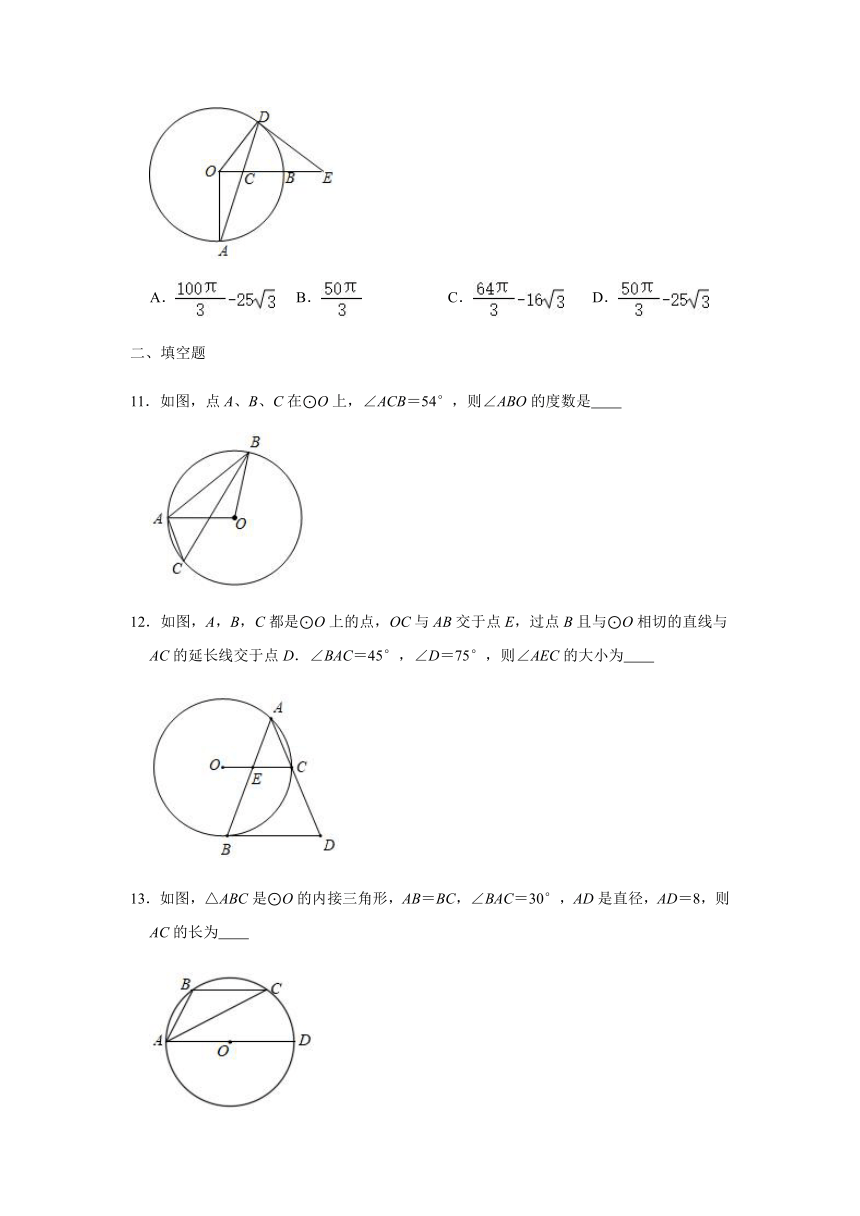
11.如图,点A、B、C在⊙O上,∠ACB=54°,则∠ABO的度数是
12.如图,A,B,C都是⊙O上的点,OC与AB交于点E,过点B且与⊙O相切的直线与AC的延长线交于点D.∠BAC=45°,∠D=75°,则∠AEC的大小为
13.如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
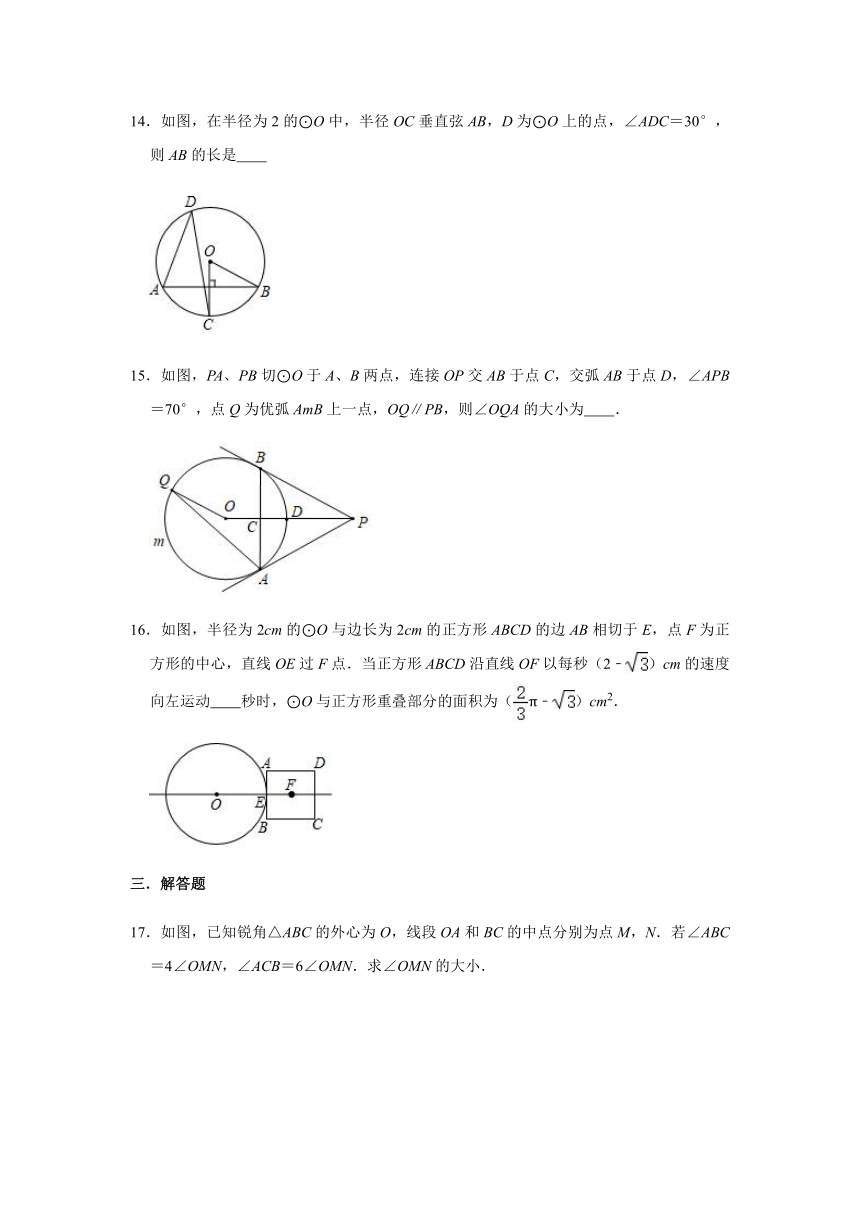
14.如图,在半径为2的⊙O中,半径OC垂直弦AB,D为⊙O上的点,∠ADC=30°,则AB的长是
15.如图,PA、PB切⊙O于A、B两点,连接OP交AB于点C,交弧AB于点D,∠APB=70°,点Q为优弧AmB上一点,OQ∥PB,则∠OQA的大小为 .
16.如图,半径为2cm的⊙O与边长为2cm的正方形ABCD的边AB相切于E,点F为正方形的中心,直线OE过F点.当正方形ABCD沿直线OF以每秒(2﹣)cm的速度向左运动 秒时,⊙O与正方形重叠部分的面积为(π﹣)cm2.
三.解答题
17.如图,已知锐角△ABC的外心为O,线段OA和BC的中点分别为点M,N.若∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN的大小.
18.如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
19.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E.F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2,BF=2,求⊙O的半径.
20.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为20,求线段AC、AB的长.
21.如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E.
(1)求证:DE与⊙O相切;
(2)若AB=5,BE=4,求BD的长;
(3)请用线段AB、BE表示CE的长,并说明理由.
22.如图①,AB为⊙O的直径,点C在⊙O上,AD平分∠CAB,AD与BC交于点F,过点D作DE⊥AB于点E.
(1)求证:BC=2DE;
(2)如图②,连接OF,若∠AFO=45°,半径为2时,求AC的长.
23.如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
参考答案
一.选择题
1.A、B、C分别表示三个村庄,AB=1700米,BC=800米,AC=1500米,某社区拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB的中点
B.BC的中点
C.AC的中点
D.∠C的平分线与AB的交点
【解答】解:∵AB=1700米,BC=800米,AC=1500米,
∴BC2+AC2=AB2,
∴∠C=90°,
根据直角三角形斜边上的中线等于斜边的一半得出活动中心P的位置应为斜边AB的中点,
故选:A.
2.如图,⊙O中,若OA⊥BC、∠AOB=66°,则∠ADC的度数为( )
A.33°
B.56°
C.57°
D.66°
【解答】解:如图,连接OC,OB.
∵OA⊥BC,
∴=,
∴∠AOC=∠AOB=66°,
∴∠ADC=∠AOC=33°,
故选:A.
3.如图,AB是直径,C、D为圆上的点,已知∠D为30°,则∠CAB的度数为( )
A.45°
B.50°
C.55°
D.60°
【解答】解:∵∠D=30°,圆周角∠D和∠B都与相对,
∴∠B=∠D=30°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB=180°﹣∠B﹣∠ACB=180°﹣30°﹣90°=60°,
故选:D.
4.如图所示,四边形ABCD是圆O的内接四边形,∠A=45°,BC=4,CD=2,则弦BD的长为( )
A.2
B.3
C.
D.2
【解答】解:如图,过点D作DE⊥BC交BC的延长线于E.
∵∠A+∠BCD=180°,∠A=45°,
∴∠BCD=135°,
∴∠DCE=45°,
∵∠E=90°,CD=2,
∴CE=ED=2,BE=CE+BC=6,
在Rt△BED中,∵∠E=90°,BE=6,DE=2,
∴BD===2,
故选:D.
5.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则的长为( )
A.2π
B.4π
C.
D.π
【解答】解:∵∠AOC:∠AOD:∠DOB=2:7:11,∠AOD+∠DOB=180°,
∴∠AOD=×180°=70°,∠DOB=110°,∠COA=20°,
∴∠COD=∠COA+∠AOD=90°,
∵OD=OC,CD=4,
∴2OD2=42,
∴OD=2,
∴的长是==,
故选:D.
6.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )
A.h=R+r
B.R=2r
C.r=a
D.R=a
【解答】解:如图,∵△ABC是等边三角形,
∴△ABC的内切圆和外接圆是同心圆,圆心为O,
设OE=r,AO=R,AD=h,
∴h=R+r,故A正确;
∵AD⊥BC,
∴∠DAC=∠BAC=×60°=30°,
在Rt△AOE中,
∴R=2r,故B正确;
∵OD=OE=r,
∵AB=AC=BC=a,
∴AE=AC=a,
∴(a)2+r2=(2r)2,(a)2+(R)2=R2,
∴r=,R=a,故C错误,D正确;
故选:C.
7.如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125°
B.130°
C.135°
D.140°
【解答】解:连接OA,OB,OC,
∵∠BDC=50°,
∴∠BOC=2∠BDC=100°,
∵,
∴∠BOC=∠AOC=100°,
∴∠ABC=∠AOC=50°,
∴∠ADC=180°﹣∠ABC=130°.
故选:B.
8.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55°
B.65°
C.60°
D.75°
【解答】解:连接CD,
∵∠A=50°,
∴∠CDB=180°﹣∠A=130°,
∵E是边BC的中点,
∴OD⊥BC,
∴BD=CD,
∴∠ODB=∠ODC=BDC=65°,
故选:B.
9.如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
【解答】解:连接OD、OE,
∵OC=OA,
∴△OAC是等腰三角形,
∵点D为弦AC的中点,
∴∠DOC=40°,∠BOC=100°,
设∠BOE=x,则∠COE=100°﹣x,∠DOE=100°﹣x+40°,
∵OC=OE,∠COE=100°﹣x,
∴∠OEC=∠OCE=40°+x,
∵OD<OE,∠DOE=100°﹣x+40°=140°﹣x,
∴∠OED<20°+x,
∴∠CED=∠OEC﹣∠OED>(40°+x)﹣(20°+x)=20°,
∵∠CED<∠ABC=40°,
∴20°<∠CED<40°
故选:C.
10.如图,已知⊙O的半径为10,A、B是⊙O上的两点,∠AOB=90°,C是射线OB上一个动点,连结AC并延长交⊙O于点D,过点D作DE⊥OD交OB的延长线于点E.当∠A从30°增大到60°时,弦AD在圆内扫过的面积是( )
A.
B.
C.
D.
【解答】解:过点D作AO的垂线,交AO的延长线于F.
当∠A=30°时,∠DOF=60°,DF=OD?sin60°=10×=5,
S弓形ABD=﹣×10×5=π﹣25,
当∠A=60°时,
过点D'作D'F⊥OA于F',连接OD',
∠D'OF'=60°,D'F'=5,
S弓形ABD'=﹣×10×5=π﹣25,
∴S=π﹣25﹣(π﹣25)=π.
故选:B.
二、填空题
11.如图,点A、B、C在⊙O上,∠ACB=54°,则∠ABO的度数是
【解答】解:∵∠ACB=54°,
∴圆心角∠AOB=2∠ACB=108°,
∵OB=OA,
∴∠ABO=∠BAO=(180°﹣∠AOB)=36°,
12.如图,A,B,C都是⊙O上的点,OC与AB交于点E,过点B且与⊙O相切的直线与AC的延长线交于点D.∠BAC=45°,∠D=75°,则∠AEC的大小为
【解答】解:∵∠BAC=45°,∠D=75°,
∴∠ABD=180°﹣45°﹣75°=60°,
连接OB,
∵BD是⊙O的切线,
∴∠OBD=90°,
∵∠BAC=45°,
∴∠BOC=90°,
∴∠BOC+∠OBD=180°,
∴OC∥BD,
∴∠AEC=∠ABD=60°,
13.如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
【解答】解:连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,
∴∠D=180°﹣∠B=60°,
∵AD是直径,
∴∠ACD=90°,
∵∠CAD=30°,AD=8,
∴CD=AD=4,
∴AC===4,
14.如图,在半径为2的⊙O中,半径OC垂直弦AB,D为⊙O上的点,∠ADC=30°,则AB的长是
【解答】解:设半径OC⊥弦AB于点E,
∴=,
∴∠D=∠BOC=30°,
∴∠BOC=60°,
∵OB=2,
∴AE=EB=OB?sin60°=,
∴AB=2AE=2,
15.如图,PA、PB切⊙O于A、B两点,连接OP交AB于点C,交弧AB于点D,∠APB=70°,点Q为优弧AmB上一点,OQ∥PB,则∠OQA的大小为 .
【解答】解:如图,连接OA.
∵PA,PB是⊙O的切线,
∴∠OPB=∠OPA=∠APB=35°,PA⊥OA,
∴∠OAP=90°,
∴∠POA=90°﹣35°=55°,
∵OQ∥PB,
∴∠POQ=180°﹣∠OPB=145°,
∴AOQ=360°﹣145°﹣55°=160°,
∵OQ=OA,
∴∠OQA=∠OAQ=(180°﹣∠AOQ)=10°,
故答案为10°.
16.如图,半径为2cm的⊙O与边长为2cm的正方形ABCD的边AB相切于E,点F为正方形的中心,直线OE过F点.当正方形ABCD沿直线OF以每秒(2﹣)cm的速度向左运动 秒时,⊙O与正方形重叠部分的面积为(π﹣)cm2.
【解答】解:如图1中,当点A,B落在⊙O上时,⊙O与正方形重叠部分的面积为(π﹣)cm2
此时,运动时间t=(2﹣)÷(2﹣)=1(秒)
如图2中,当点C,D落在⊙O上时,⊙O与正方形重叠部分的面积为(π﹣)cm2
此时,运动时间t=[4+2﹣(2﹣)]÷(2﹣)=(11+6)(秒),
综上所述,满足条件的t的值为1秒或(11+6)秒.
故答案为1或(11+6).
三.解答题
17.如图,已知锐角△ABC的外心为O,线段OA和BC的中点分别为点M,N.若∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN的大小.
【解答】解:连接OC.设∠OMN=x,则∠ABC=4x,∠ACB=6x;
∴∠NOC=180°﹣10x,∠AOC=8x,
∴∠ONM=180°﹣(180°﹣10x+8x+x)=x,
∴△MON为等腰三角形,
∴;
∴∠OBN=30°,
∴180°﹣10x=60°,
∴x=12°.
18.如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
【解答】(1)证明:∵AE=DE,OC是半径,
∴=,
∴∠CAD=∠CBA.
(2)解:∵AB是直径,
∴∠ACB=90°,
∵AE=DE,
∴OC⊥AD,
∴∠AEC=90°,
∴∠AEC=∠ACB,
∴△AEC∽△BCA,
∴=,
∴=,
∴CE=3.6,
∵OC=AB=5,
∴OE=OC﹣EC=5﹣3.6=1.4.
19.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E.F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2,BF=2,求⊙O的半径.
【解答】解:(1)线BC与⊙O的位置关系是相切,
理由是:连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠CAB,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC,
∵OD为半径,
∴线BC与⊙O的位置关系是相切;
(2)设⊙O的半径为R,
则OD=OF=R,
在Rt△BDO中,由勾股定理得:OB2=BD2+OD2,
即(R+2)2=(2)2+R2,
解得:R=4,
即⊙O的半径是4.
20.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为20,求线段AC、AB的长.
【解答】证明:(1)连接OC.
∵点C在⊙O上,OA=OC,
∴∠OCA=∠OAC,
∵CD⊥PA,
∴∠CDA=90°,
∴∠CAD+∠DCA=90°,
∵AC平分∠PAE,
∴∠DAC=∠CAO,
∴∠DCO=∠DCA+∠ACO=∠DCA+∠DAC=90°,
∴CD是⊙O切线.
(2)作OF⊥AB于F,
∴∠OCD=∠CDF=∠OFD=90°,
∴四边形CDFO是矩形,
∴OC=FD,OF=CD,
∵CD=2AD,设AD=x,则OF=CD=2x,
∵DF=OC=10,
∴AF=10﹣x,
在Rt△AOF中,AF2+OF2=OA2,
∴(10﹣x)2+(2x)2=102,
解得x=4或0(舍弃),
∴AD=4,AF=6,AC=4,
∵OF⊥AB,
∴AB=2AF=12.
21.如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E.
(1)求证:DE与⊙O相切;
(2)若AB=5,BE=4,求BD的长;
(3)请用线段AB、BE表示CE的长,并说明理由.
【解答】(1)证明:连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BE,
∵BE⊥DE,
∴OD⊥DE,
∴DE与⊙O相切;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵BE⊥DE,
∴∠ADB=∠BED=90°,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴△ABD∽△DBE,
∴,
∴=,
∴BD=2;
(3)解:结论CE=AB﹣BE,
理由:过D作DH⊥AB于H,
∵BD平分∠ABC,DE⊥BE,
∴DH=DE,
在Rt△BED与Rt△BHD中,,
∴Rt△BED≌Rt△BHD(HL),
∴BH=BE,
∵∠DCE=∠A,∠DHA=∠DEC=90°,
∴△ADH≌△CDE(AAS),
∴AH=CE,
∵AB=AH+BH,
∴AB=BE+CE,
∴CE=AB﹣BE.
22.如图①,AB为⊙O的直径,点C在⊙O上,AD平分∠CAB,AD与BC交于点F,过点D作DE⊥AB于点E.
(1)求证:BC=2DE;
(2)如图②,连接OF,若∠AFO=45°,半径为2时,求AC的长.
【解答】(1)证明:如图①中,延长DE交⊙O于G,连接AG.
∵AB⊥DG,AB是直径,
∴=,DE=EG,
∵AD平分∠CAB,
∴∠CAD=∠DAB,
∴=,
∴=,
∴BC=DG=2DE.
(2)解:如图②中,作FR⊥AB于R,OS⊥AD于S.
∵AD平分∠CAB,FC⊥AC,FR⊥AB,
∴∠CAD=∠BAD=x,FC=FR,
∴∠FBO=90°﹣2x,
∵∠AFO=45°,
∴∠FOB=45°+x,
∴∠OFB=180°﹣(90°﹣2x)﹣(45°+x)=45°+x,
∴∠FOB=∠OFB
∴BF=BO=OA,
∵∠FRB=∠ACB=90°,∠FBR=∠ABC,
∴△BFR∽△BAC,
∴==,
∴AC=2FR=2FC,
∴tan∠FAR=tan∠FAC=,
设SO=t,AS=2t,SF=SO=t,
则t2+4t2=4,
∵t>0,
∴t=,
∴AF=3t=,设CF=m,则AC=2m,
则有5m2=,
∵m>0,
∴m=,
∴AC=2m=.
23.如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
【解答】(1)证明:连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴EF是⊙O切线.
(2)解:在△FEA与△FBE中,
∵∠F=∠F,∠FEA=∠FBE,
∴△FEA∽△FBE,
∴==,
∴AF?BF=EF?EF,
∴AF×(AF+15)=10×10,
解得AF=5.
∴BF=20.
∴=,
∴BE=2AE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴AE2+BE2=152,
∴AE2+(2AE)2=225,
∴AE=3.
圆
单元测试题
一.选择题
1.A、B、C分别表示三个村庄,AB=1700米,BC=800米,AC=1500米,某社区拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB的中点
B.BC的中点
C.AC的中点
D.∠C的平分线与AB的交点
2.如图,⊙O中,若OA⊥BC、∠AOB=66°,则∠ADC的度数为( )
A.33°
B.56°
C.57°
D.66°
3.如图,AB是直径,C、D为圆上的点,已知∠D为30°,则∠CAB的度数为( )
A.45°
B.50°
C.55°
D.60°
4.如图所示,四边形ABCD是圆O的内接四边形,∠A=45°,BC=4,CD=2,则弦BD的长为( )
A.2
B.3
C.
D.2
5.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则的长为( )
A.2π
B.4π
C.
D.π
6.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )
A.h=R+r
B.R=2r
C.r=a
D.R=a
7.如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125°
B.130°
C.135°
D.140°
8.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55°
B.65°
C.60°
D.75°
9.如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
10.如图,已知⊙O的半径为10,A、B是⊙O上的两点,∠AOB=90°,C是射线OB上一个动点,连结AC并延长交⊙O于点D,过点D作DE⊥OD交OB的延长线于点E.当∠A从30°增大到60°时,弦AD在圆内扫过的面积是( )
A.
B.
C.
D.
二、填空题
11.如图,点A、B、C在⊙O上,∠ACB=54°,则∠ABO的度数是
12.如图,A,B,C都是⊙O上的点,OC与AB交于点E,过点B且与⊙O相切的直线与AC的延长线交于点D.∠BAC=45°,∠D=75°,则∠AEC的大小为
13.如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
14.如图,在半径为2的⊙O中,半径OC垂直弦AB,D为⊙O上的点,∠ADC=30°,则AB的长是
15.如图,PA、PB切⊙O于A、B两点,连接OP交AB于点C,交弧AB于点D,∠APB=70°,点Q为优弧AmB上一点,OQ∥PB,则∠OQA的大小为 .
16.如图,半径为2cm的⊙O与边长为2cm的正方形ABCD的边AB相切于E,点F为正方形的中心,直线OE过F点.当正方形ABCD沿直线OF以每秒(2﹣)cm的速度向左运动 秒时,⊙O与正方形重叠部分的面积为(π﹣)cm2.
三.解答题
17.如图,已知锐角△ABC的外心为O,线段OA和BC的中点分别为点M,N.若∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN的大小.
18.如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
19.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E.F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2,BF=2,求⊙O的半径.
20.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为20,求线段AC、AB的长.
21.如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E.
(1)求证:DE与⊙O相切;
(2)若AB=5,BE=4,求BD的长;
(3)请用线段AB、BE表示CE的长,并说明理由.
22.如图①,AB为⊙O的直径,点C在⊙O上,AD平分∠CAB,AD与BC交于点F,过点D作DE⊥AB于点E.
(1)求证:BC=2DE;
(2)如图②,连接OF,若∠AFO=45°,半径为2时,求AC的长.
23.如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
参考答案
一.选择题
1.A、B、C分别表示三个村庄,AB=1700米,BC=800米,AC=1500米,某社区拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB的中点
B.BC的中点
C.AC的中点
D.∠C的平分线与AB的交点
【解答】解:∵AB=1700米,BC=800米,AC=1500米,
∴BC2+AC2=AB2,
∴∠C=90°,
根据直角三角形斜边上的中线等于斜边的一半得出活动中心P的位置应为斜边AB的中点,
故选:A.
2.如图,⊙O中,若OA⊥BC、∠AOB=66°,则∠ADC的度数为( )
A.33°
B.56°
C.57°
D.66°
【解答】解:如图,连接OC,OB.
∵OA⊥BC,
∴=,
∴∠AOC=∠AOB=66°,
∴∠ADC=∠AOC=33°,
故选:A.
3.如图,AB是直径,C、D为圆上的点,已知∠D为30°,则∠CAB的度数为( )
A.45°
B.50°
C.55°
D.60°
【解答】解:∵∠D=30°,圆周角∠D和∠B都与相对,
∴∠B=∠D=30°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB=180°﹣∠B﹣∠ACB=180°﹣30°﹣90°=60°,
故选:D.
4.如图所示,四边形ABCD是圆O的内接四边形,∠A=45°,BC=4,CD=2,则弦BD的长为( )
A.2
B.3
C.
D.2
【解答】解:如图,过点D作DE⊥BC交BC的延长线于E.
∵∠A+∠BCD=180°,∠A=45°,
∴∠BCD=135°,
∴∠DCE=45°,
∵∠E=90°,CD=2,
∴CE=ED=2,BE=CE+BC=6,
在Rt△BED中,∵∠E=90°,BE=6,DE=2,
∴BD===2,
故选:D.
5.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则的长为( )
A.2π
B.4π
C.
D.π
【解答】解:∵∠AOC:∠AOD:∠DOB=2:7:11,∠AOD+∠DOB=180°,
∴∠AOD=×180°=70°,∠DOB=110°,∠COA=20°,
∴∠COD=∠COA+∠AOD=90°,
∵OD=OC,CD=4,
∴2OD2=42,
∴OD=2,
∴的长是==,
故选:D.
6.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )
A.h=R+r
B.R=2r
C.r=a
D.R=a
【解答】解:如图,∵△ABC是等边三角形,
∴△ABC的内切圆和外接圆是同心圆,圆心为O,
设OE=r,AO=R,AD=h,
∴h=R+r,故A正确;
∵AD⊥BC,
∴∠DAC=∠BAC=×60°=30°,
在Rt△AOE中,
∴R=2r,故B正确;
∵OD=OE=r,
∵AB=AC=BC=a,
∴AE=AC=a,
∴(a)2+r2=(2r)2,(a)2+(R)2=R2,
∴r=,R=a,故C错误,D正确;
故选:C.
7.如图,四边形ABCD内接于⊙O,连接BD.若,∠BDC=50°,则∠ADC的度数是( )
A.125°
B.130°
C.135°
D.140°
【解答】解:连接OA,OB,OC,
∵∠BDC=50°,
∴∠BOC=2∠BDC=100°,
∵,
∴∠BOC=∠AOC=100°,
∴∠ABC=∠AOC=50°,
∴∠ADC=180°﹣∠ABC=130°.
故选:B.
8.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55°
B.65°
C.60°
D.75°
【解答】解:连接CD,
∵∠A=50°,
∴∠CDB=180°﹣∠A=130°,
∵E是边BC的中点,
∴OD⊥BC,
∴BD=CD,
∴∠ODB=∠ODC=BDC=65°,
故选:B.
9.如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10°
B.20°
C.30°
D.40°
【解答】解:连接OD、OE,
∵OC=OA,
∴△OAC是等腰三角形,
∵点D为弦AC的中点,
∴∠DOC=40°,∠BOC=100°,
设∠BOE=x,则∠COE=100°﹣x,∠DOE=100°﹣x+40°,
∵OC=OE,∠COE=100°﹣x,
∴∠OEC=∠OCE=40°+x,
∵OD<OE,∠DOE=100°﹣x+40°=140°﹣x,
∴∠OED<20°+x,
∴∠CED=∠OEC﹣∠OED>(40°+x)﹣(20°+x)=20°,
∵∠CED<∠ABC=40°,
∴20°<∠CED<40°
故选:C.
10.如图,已知⊙O的半径为10,A、B是⊙O上的两点,∠AOB=90°,C是射线OB上一个动点,连结AC并延长交⊙O于点D,过点D作DE⊥OD交OB的延长线于点E.当∠A从30°增大到60°时,弦AD在圆内扫过的面积是( )
A.
B.
C.
D.
【解答】解:过点D作AO的垂线,交AO的延长线于F.
当∠A=30°时,∠DOF=60°,DF=OD?sin60°=10×=5,
S弓形ABD=﹣×10×5=π﹣25,
当∠A=60°时,
过点D'作D'F⊥OA于F',连接OD',
∠D'OF'=60°,D'F'=5,
S弓形ABD'=﹣×10×5=π﹣25,
∴S=π﹣25﹣(π﹣25)=π.
故选:B.
二、填空题
11.如图,点A、B、C在⊙O上,∠ACB=54°,则∠ABO的度数是
【解答】解:∵∠ACB=54°,
∴圆心角∠AOB=2∠ACB=108°,
∵OB=OA,
∴∠ABO=∠BAO=(180°﹣∠AOB)=36°,
12.如图,A,B,C都是⊙O上的点,OC与AB交于点E,过点B且与⊙O相切的直线与AC的延长线交于点D.∠BAC=45°,∠D=75°,则∠AEC的大小为
【解答】解:∵∠BAC=45°,∠D=75°,
∴∠ABD=180°﹣45°﹣75°=60°,
连接OB,
∵BD是⊙O的切线,
∴∠OBD=90°,
∵∠BAC=45°,
∴∠BOC=90°,
∴∠BOC+∠OBD=180°,
∴OC∥BD,
∴∠AEC=∠ABD=60°,
13.如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
【解答】解:连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,
∴∠D=180°﹣∠B=60°,
∵AD是直径,
∴∠ACD=90°,
∵∠CAD=30°,AD=8,
∴CD=AD=4,
∴AC===4,
14.如图,在半径为2的⊙O中,半径OC垂直弦AB,D为⊙O上的点,∠ADC=30°,则AB的长是
【解答】解:设半径OC⊥弦AB于点E,
∴=,
∴∠D=∠BOC=30°,
∴∠BOC=60°,
∵OB=2,
∴AE=EB=OB?sin60°=,
∴AB=2AE=2,
15.如图,PA、PB切⊙O于A、B两点,连接OP交AB于点C,交弧AB于点D,∠APB=70°,点Q为优弧AmB上一点,OQ∥PB,则∠OQA的大小为 .
【解答】解:如图,连接OA.
∵PA,PB是⊙O的切线,
∴∠OPB=∠OPA=∠APB=35°,PA⊥OA,
∴∠OAP=90°,
∴∠POA=90°﹣35°=55°,
∵OQ∥PB,
∴∠POQ=180°﹣∠OPB=145°,
∴AOQ=360°﹣145°﹣55°=160°,
∵OQ=OA,
∴∠OQA=∠OAQ=(180°﹣∠AOQ)=10°,
故答案为10°.
16.如图,半径为2cm的⊙O与边长为2cm的正方形ABCD的边AB相切于E,点F为正方形的中心,直线OE过F点.当正方形ABCD沿直线OF以每秒(2﹣)cm的速度向左运动 秒时,⊙O与正方形重叠部分的面积为(π﹣)cm2.
【解答】解:如图1中,当点A,B落在⊙O上时,⊙O与正方形重叠部分的面积为(π﹣)cm2
此时,运动时间t=(2﹣)÷(2﹣)=1(秒)
如图2中,当点C,D落在⊙O上时,⊙O与正方形重叠部分的面积为(π﹣)cm2
此时,运动时间t=[4+2﹣(2﹣)]÷(2﹣)=(11+6)(秒),
综上所述,满足条件的t的值为1秒或(11+6)秒.
故答案为1或(11+6).
三.解答题
17.如图,已知锐角△ABC的外心为O,线段OA和BC的中点分别为点M,N.若∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN的大小.
【解答】解:连接OC.设∠OMN=x,则∠ABC=4x,∠ACB=6x;
∴∠NOC=180°﹣10x,∠AOC=8x,
∴∠ONM=180°﹣(180°﹣10x+8x+x)=x,
∴△MON为等腰三角形,
∴;
∴∠OBN=30°,
∴180°﹣10x=60°,
∴x=12°.
18.如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
【解答】(1)证明:∵AE=DE,OC是半径,
∴=,
∴∠CAD=∠CBA.
(2)解:∵AB是直径,
∴∠ACB=90°,
∵AE=DE,
∴OC⊥AD,
∴∠AEC=90°,
∴∠AEC=∠ACB,
∴△AEC∽△BCA,
∴=,
∴=,
∴CE=3.6,
∵OC=AB=5,
∴OE=OC﹣EC=5﹣3.6=1.4.
19.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E.F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2,BF=2,求⊙O的半径.
【解答】解:(1)线BC与⊙O的位置关系是相切,
理由是:连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠CAB,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC,
∵OD为半径,
∴线BC与⊙O的位置关系是相切;
(2)设⊙O的半径为R,
则OD=OF=R,
在Rt△BDO中,由勾股定理得:OB2=BD2+OD2,
即(R+2)2=(2)2+R2,
解得:R=4,
即⊙O的半径是4.
20.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为20,求线段AC、AB的长.
【解答】证明:(1)连接OC.
∵点C在⊙O上,OA=OC,
∴∠OCA=∠OAC,
∵CD⊥PA,
∴∠CDA=90°,
∴∠CAD+∠DCA=90°,
∵AC平分∠PAE,
∴∠DAC=∠CAO,
∴∠DCO=∠DCA+∠ACO=∠DCA+∠DAC=90°,
∴CD是⊙O切线.
(2)作OF⊥AB于F,
∴∠OCD=∠CDF=∠OFD=90°,
∴四边形CDFO是矩形,
∴OC=FD,OF=CD,
∵CD=2AD,设AD=x,则OF=CD=2x,
∵DF=OC=10,
∴AF=10﹣x,
在Rt△AOF中,AF2+OF2=OA2,
∴(10﹣x)2+(2x)2=102,
解得x=4或0(舍弃),
∴AD=4,AF=6,AC=4,
∵OF⊥AB,
∴AB=2AF=12.
21.如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E.
(1)求证:DE与⊙O相切;
(2)若AB=5,BE=4,求BD的长;
(3)请用线段AB、BE表示CE的长,并说明理由.
【解答】(1)证明:连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BE,
∵BE⊥DE,
∴OD⊥DE,
∴DE与⊙O相切;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵BE⊥DE,
∴∠ADB=∠BED=90°,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴△ABD∽△DBE,
∴,
∴=,
∴BD=2;
(3)解:结论CE=AB﹣BE,
理由:过D作DH⊥AB于H,
∵BD平分∠ABC,DE⊥BE,
∴DH=DE,
在Rt△BED与Rt△BHD中,,
∴Rt△BED≌Rt△BHD(HL),
∴BH=BE,
∵∠DCE=∠A,∠DHA=∠DEC=90°,
∴△ADH≌△CDE(AAS),
∴AH=CE,
∵AB=AH+BH,
∴AB=BE+CE,
∴CE=AB﹣BE.
22.如图①,AB为⊙O的直径,点C在⊙O上,AD平分∠CAB,AD与BC交于点F,过点D作DE⊥AB于点E.
(1)求证:BC=2DE;
(2)如图②,连接OF,若∠AFO=45°,半径为2时,求AC的长.
【解答】(1)证明:如图①中,延长DE交⊙O于G,连接AG.
∵AB⊥DG,AB是直径,
∴=,DE=EG,
∵AD平分∠CAB,
∴∠CAD=∠DAB,
∴=,
∴=,
∴BC=DG=2DE.
(2)解:如图②中,作FR⊥AB于R,OS⊥AD于S.
∵AD平分∠CAB,FC⊥AC,FR⊥AB,
∴∠CAD=∠BAD=x,FC=FR,
∴∠FBO=90°﹣2x,
∵∠AFO=45°,
∴∠FOB=45°+x,
∴∠OFB=180°﹣(90°﹣2x)﹣(45°+x)=45°+x,
∴∠FOB=∠OFB
∴BF=BO=OA,
∵∠FRB=∠ACB=90°,∠FBR=∠ABC,
∴△BFR∽△BAC,
∴==,
∴AC=2FR=2FC,
∴tan∠FAR=tan∠FAC=,
设SO=t,AS=2t,SF=SO=t,
则t2+4t2=4,
∵t>0,
∴t=,
∴AF=3t=,设CF=m,则AC=2m,
则有5m2=,
∵m>0,
∴m=,
∴AC=2m=.
23.如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
【解答】(1)证明:连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴EF是⊙O切线.
(2)解:在△FEA与△FBE中,
∵∠F=∠F,∠FEA=∠FBE,
∴△FEA∽△FBE,
∴==,
∴AF?BF=EF?EF,
∴AF×(AF+15)=10×10,
解得AF=5.
∴BF=20.
∴=,
∴BE=2AE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴AE2+BE2=152,
∴AE2+(2AE)2=225,
∴AE=3.
