初中数学青岛版九年级上册2.5解直角三角形的应用同步练习(Word版解析版)
文档属性
| 名称 | 初中数学青岛版九年级上册2.5解直角三角形的应用同步练习(Word版解析版) | 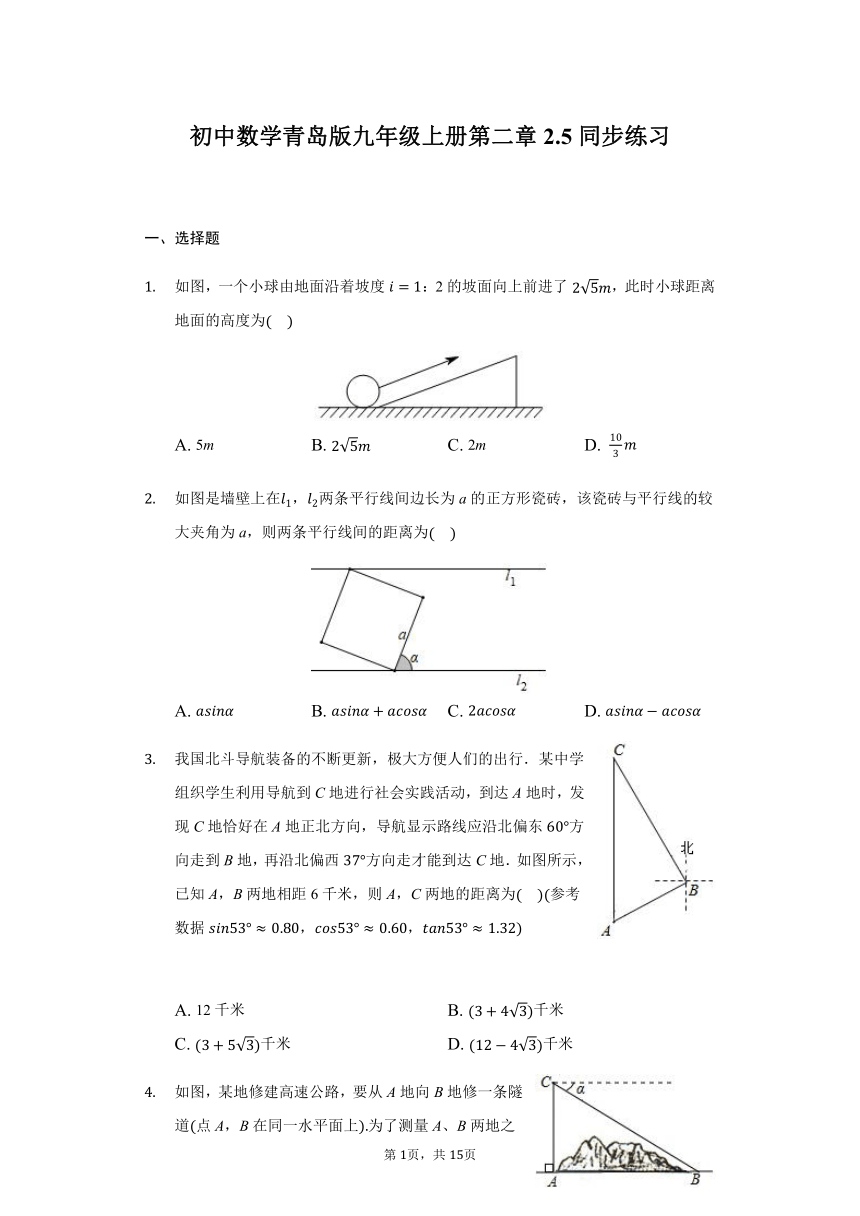 | |
| 格式 | zip | ||
| 文件大小 | 181.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 14:29:38 | ||
图片预览




文档简介
初中数学青岛版九年级上册第二章2.5同步练习
一、选择题
如图,一个小球由地面沿着坡度:2的坡面向上前进了,此时小球距离地面的高度为
A.
5m
B.
C.
2m
D.
如图是墙壁上在,两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为a,则两条平行线间的距离为
A.
B.
C.
D.
我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东方向走到B地,再沿北偏西方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为参考数据,,
A.
12千米
B.
千米
C.
千米
D.
千米
如图,某地修建高速公路,要从A地向B地修一条隧道点A,B在同一水平面上为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为,则A,B两地之间的距离为
A.
400米
B.
米
C.
1600米
D.
米
如图,撬钉子的工具是一个杠杆,动力臂,阻力臂,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是
A.
越来越小
B.
不变
C.
越来越大
D.
无法确定
从一艘船上测得海岸上高为42米的灯塔顶部的仰角为时,船离灯塔的水平距离是
A.
米
B.
米
C.
21米
D.
42米
如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节AE间的距离.若AE间的距离调节到60cm,菱形的边长,则的度数是
A.
B.
C.
D.
某长江大桥采用低塔斜拉桥桥型如甲图,图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是,拉索BD与水平桥面的夹角是,两拉索底端距离米,则立柱BC的高为
A.
米
B.
10米
C.
米
D.
20米
如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西方向,则河宽的长可以表示为
A.
米
B.
米
C.
200sin?米
D.
米
如图,小刚家在甲楼,他想利用最近所学知识测量对面的乙楼的高度,小刚在甲楼楼底B点测得乙楼楼顶C点的仰角为,当他爬上楼顶,在A点处测得乙楼D点的仰角为若,,则乙楼的高度CE为参考数据:,,精确到
A.
B.
C.
D.
二、填空题
一名长跑运动员沿着斜角为的斜坡,从B点跑至A点,已知米,则运动员的高度下降了______米.
如图是一个地铁站入口的双翼闸机.它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘,且与闸机侧立面夹角当双翼收起时,可以通过闸机的物体的最大宽度为______cm.
如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为,测得底部C的俯角为,此时航拍无人机与该建筑物的水平距离AD为120m,那么该建筑物的高度BC约为______结果保留整数,.
某人沿着有一定坡度的坡面前进了6米,此时他在垂直方向的距离上升了2米,则这个坡面的坡度为______.
三、解答题
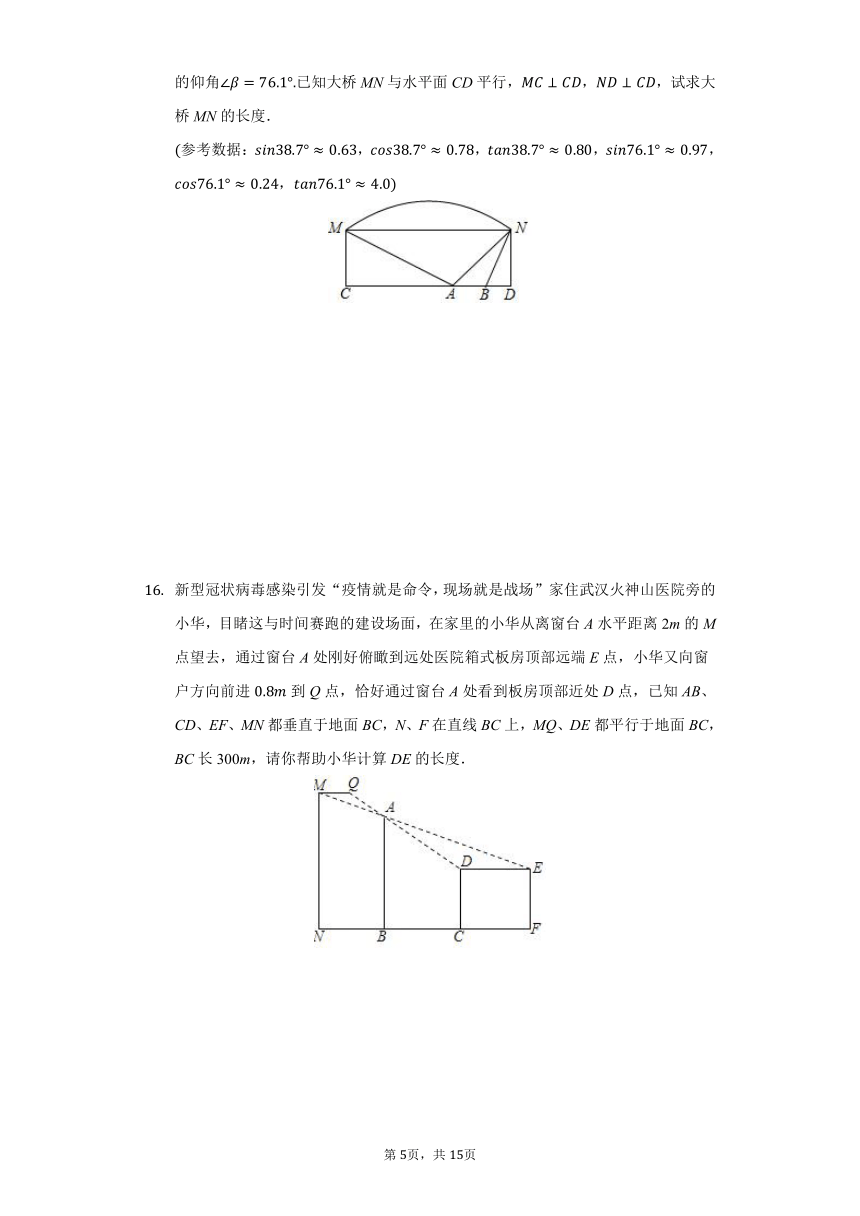
为推进山区经济发展,往往首先要架桥修路.某工程队计划将两座山的山腰M、N两点处连接起来修建一座大桥MN,现需要测量大桥MN的长度.如图,测量小组在山谷底部A处测得观察M处时的仰角,转身观察N处时的仰角:然后测量小组向前走了50米来到点B处,在B处测得观察N处时的仰角已知大桥MN与水平面CD平行,,,试求大桥MN的长度.
参考数据:,,,,,
新型冠状病毒感染引发“疫情就是命令,现场就是战场”家住武汉火神山医院旁的小华,目睹这与时间赛跑的建设场面,在家里的小华从离窗台A水平距离2m的M点望去,通过窗台A处刚好俯瞰到远处医院箱式板房顶部远端E点,小华又向窗户方向前进到Q点,恰好通过窗台A处看到板房顶部近处D点,已知AB、CD、EF、MN都垂直于地面BC,N、F在直线BC上,MQ、DE都平行于地面BC,BC长300m,请你帮助小华计算DE的长度.
如图,学校的教学楼对面是一幢办公楼,教学楼与办公楼的水平距离,卓玛在教学楼顶部A处测得办公楼顶部D处的俯角为,测得办公楼底部C处俯角为,求办公楼的高结果保留根号
答案和解析
1.【答案】C
【解析】解:,.
设,,
由勾股定理得,,
即,
解得:,
故小球距离地面的高度为2m.
故选:C.
可利用勾股定理及所给的比值得到所求的线段长.
本题主要考查了勾股定理在直角三角形中的运用,i的定义,能从实际问题中整理出直角三角形是解答本题的关键.
2.【答案】B
【解析】解:如图,过B作于点E,EF与交于点F,则,
四边形ABCD是正方形,
,,
,
,
,
≌,
,
在中,,,
,
,
即两条平行线间的距离为,
故选:B.
如图,过B作于点E,EF与交于点F,则,证明≌,得,解便可得结果.
本题考查解直角三角形,正方形的性质,全等三角形的性质与判定,解题的关键是熟练运用锐角三角函数的定义,本题属于中等题型.
3.【答案】B
【解析】解:如图,作于点D,
根据题意可知:
在中,,,
,,
在中,,
,
.
则A,C两地的距离为千米.
故选:B.
作于点D,根据题意可得,,,,再根据锐角三角函数即可求出AD和CD的值,进而求出A,C两地的距离.
本题考查了解直角三角形的应用方向角问题,解决本题的关键是掌握方向角定义.
4.【答案】D
【解析】解:根据题意可知:
,,,
米.
答:A,B两地之间的距离为米.
故选:D.
根据题意可得,,,,进而可求A,B两地之间的距离.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
5.【答案】A
【解析】解:动力动力臂阻力阻力臂,
当阻力及阻力臂不变时,动力动力臂为定值,且定值,
动力随着动力臂的增大而减小,
杠杆向下运动时的度数越来越小,此时的值越来越大,
又动力臂,
此时动力臂也越来越大,
此时的动力越来越小,
故选:A.
根据杠杆原理及的值随着的减小而增大结合反比例函数的增减性即可求得答案.
本题主要考查了杠杆原理以及锐角三角函数和反比例函数的增减性等知识;熟练掌握相关知识是解决本题的关键.
6.【答案】A
【解析】解:根据题意可得:船离海岸线的距离为米
故选:A.
在直角三角形中,已知角的对边求邻边,可以用正切函数来解决.
本题考查解直角三角形的应用仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
7.【答案】C
【解析】解:连结AE,
间的距离调节到60cm,木制活动衣帽架是由三个全等的菱形构成,
,
菱形的边长,
,
,
是等边三角形,
,
.
故选:C.
连结AE,根据全等的性质可得,根据菱形的性质和等边三角形的判定可得是等边三角形,再根据等边三角形和菱形的性质即可求解.
考查了菱形的性质,全等图形,等边三角形的判定与性质,解题的关键是得到是等边三角形.
8.【答案】C
【解析】解:,,,
,
,
米,
米,
故选:C.
首先证明米,解直角三角形求出BC即可.
本题考查解直角三角形的应用,等腰三角形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
9.【答案】B
【解析】解:在中,
,,
,
,
,
即河宽米,
故选:B.
在直角三角形PQT中,利用PQ的长,以及的度数,进而得到的度数,根据三角函数即可求得PT的长.
此题考查了解直角三角形的应用方向角问题,掌握方向角与正切函数的定义是解题的关键.
10.【答案】C
【解析】解:如图,过点A作于点F,
根据题意可知:
,,
四边形ABEF是矩形,
,,
在中,,
,
在中,,
,
,
解得,
.
答:乙楼的高度CE为.
故选:C.
过点A作于点F,根据题意可得,四边形ABEF是矩形,再根据特殊角三角函数即可求出乙楼的高度.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
11.【答案】500
【解析】解:在中,
米,,
米.
故答案为:500.
根据题意,从B点跑至A点,实际下降的高度为BC,在中,求出BC的长度即可.
本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数的知识求解.
12.【答案】64
【解析】解:如图,连接AB,CD,过点A作于E,过点B作于F.
,,
四边形ABFE是平行四边形,
,
四边形AEFB是矩形,
,
,
,
,
同法可得,
,
故答案为64.
如图,连接AB,CD,过点A作于E,过点B作于求出CE,EF,DF即可解决问题.
本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线面构造直角三角形解决问题.
13.【答案】328
【解析】解:如图,在中,,,
,
在中,,
,
答:该建筑物的高度BC约为328米.
故答案为:328.
在中,根据正切函数求得,在中,求得,再根据,代入数据计算即可.
此题考查了解直角三角形的应用仰角俯角问题.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.
14.【答案】
【解析】解:由题意可得:,,
则在直角中,
,
故这个坡面的坡度为:.
故答案为:.
直接利用勾股定理得出AC的长,再利用坡角的定义得出答案.
此题主要考查了坡角的定义,正确把握坡角的定义是解题关键.
15.【答案】解:,,
,
,
四边形CDNM是矩形,
,,
在中,,
,
在中,,
,
,
,
,,
在中,,
,
米.
【解析】根据平行线的判定定理得到,推出四边形CDNM是矩形,根据矩形的性质得到,,解直角三角形即可得到结论.
本题考查了解直角三角形仰角俯角问题,矩形的判定和性质,正确的识别图形是解题的关键.
16.【答案】解:延长ED交AB于H,延长MQ交BA的延长线于T.
由题意,,
,
四边形BCDH是矩形,
,
,
,
,
,
,
.
【解析】延长ED交AB于H,延长MQ交BA的延长线于利用平行线分线段成比例定理解决问题即可.
本题考查解直角三角形的应用,平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.
17.【答案】解:过A作交CD的延长线于E,
则,
在中,,
,
,
在中,,
,
,
,
答:办公楼的高CD为
【解析】过A作交CD的延长线于E,在和中,由三角函数定义求出DE、CE的长,即可解决问题.
本题考查了解直角三角形的应用仰角俯角问题;解题的关键是借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.
第2页,共2页
第1页,共1页
一、选择题
如图,一个小球由地面沿着坡度:2的坡面向上前进了,此时小球距离地面的高度为
A.
5m
B.
C.
2m
D.
如图是墙壁上在,两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为a,则两条平行线间的距离为
A.
B.
C.
D.
我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东方向走到B地,再沿北偏西方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为参考数据,,
A.
12千米
B.
千米
C.
千米
D.
千米
如图,某地修建高速公路,要从A地向B地修一条隧道点A,B在同一水平面上为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为,则A,B两地之间的距离为
A.
400米
B.
米
C.
1600米
D.
米
如图,撬钉子的工具是一个杠杆,动力臂,阻力臂,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是
A.
越来越小
B.
不变
C.
越来越大
D.
无法确定
从一艘船上测得海岸上高为42米的灯塔顶部的仰角为时,船离灯塔的水平距离是
A.
米
B.
米
C.
21米
D.
42米
如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节AE间的距离.若AE间的距离调节到60cm,菱形的边长,则的度数是
A.
B.
C.
D.
某长江大桥采用低塔斜拉桥桥型如甲图,图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是,拉索BD与水平桥面的夹角是,两拉索底端距离米,则立柱BC的高为
A.
米
B.
10米
C.
米
D.
20米
如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西方向,则河宽的长可以表示为
A.
米
B.
米
C.
200sin?米
D.
米
如图,小刚家在甲楼,他想利用最近所学知识测量对面的乙楼的高度,小刚在甲楼楼底B点测得乙楼楼顶C点的仰角为,当他爬上楼顶,在A点处测得乙楼D点的仰角为若,,则乙楼的高度CE为参考数据:,,精确到
A.
B.
C.
D.
二、填空题
一名长跑运动员沿着斜角为的斜坡,从B点跑至A点,已知米,则运动员的高度下降了______米.
如图是一个地铁站入口的双翼闸机.它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘,且与闸机侧立面夹角当双翼收起时,可以通过闸机的物体的最大宽度为______cm.
如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为,测得底部C的俯角为,此时航拍无人机与该建筑物的水平距离AD为120m,那么该建筑物的高度BC约为______结果保留整数,.
某人沿着有一定坡度的坡面前进了6米,此时他在垂直方向的距离上升了2米,则这个坡面的坡度为______.
三、解答题
为推进山区经济发展,往往首先要架桥修路.某工程队计划将两座山的山腰M、N两点处连接起来修建一座大桥MN,现需要测量大桥MN的长度.如图,测量小组在山谷底部A处测得观察M处时的仰角,转身观察N处时的仰角:然后测量小组向前走了50米来到点B处,在B处测得观察N处时的仰角已知大桥MN与水平面CD平行,,,试求大桥MN的长度.
参考数据:,,,,,
新型冠状病毒感染引发“疫情就是命令,现场就是战场”家住武汉火神山医院旁的小华,目睹这与时间赛跑的建设场面,在家里的小华从离窗台A水平距离2m的M点望去,通过窗台A处刚好俯瞰到远处医院箱式板房顶部远端E点,小华又向窗户方向前进到Q点,恰好通过窗台A处看到板房顶部近处D点,已知AB、CD、EF、MN都垂直于地面BC,N、F在直线BC上,MQ、DE都平行于地面BC,BC长300m,请你帮助小华计算DE的长度.
如图,学校的教学楼对面是一幢办公楼,教学楼与办公楼的水平距离,卓玛在教学楼顶部A处测得办公楼顶部D处的俯角为,测得办公楼底部C处俯角为,求办公楼的高结果保留根号
答案和解析
1.【答案】C
【解析】解:,.
设,,
由勾股定理得,,
即,
解得:,
故小球距离地面的高度为2m.
故选:C.
可利用勾股定理及所给的比值得到所求的线段长.
本题主要考查了勾股定理在直角三角形中的运用,i的定义,能从实际问题中整理出直角三角形是解答本题的关键.
2.【答案】B
【解析】解:如图,过B作于点E,EF与交于点F,则,
四边形ABCD是正方形,
,,
,
,
,
≌,
,
在中,,,
,
,
即两条平行线间的距离为,
故选:B.
如图,过B作于点E,EF与交于点F,则,证明≌,得,解便可得结果.
本题考查解直角三角形,正方形的性质,全等三角形的性质与判定,解题的关键是熟练运用锐角三角函数的定义,本题属于中等题型.
3.【答案】B
【解析】解:如图,作于点D,
根据题意可知:
在中,,,
,,
在中,,
,
.
则A,C两地的距离为千米.
故选:B.
作于点D,根据题意可得,,,,再根据锐角三角函数即可求出AD和CD的值,进而求出A,C两地的距离.
本题考查了解直角三角形的应用方向角问题,解决本题的关键是掌握方向角定义.
4.【答案】D
【解析】解:根据题意可知:
,,,
米.
答:A,B两地之间的距离为米.
故选:D.
根据题意可得,,,,进而可求A,B两地之间的距离.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
5.【答案】A
【解析】解:动力动力臂阻力阻力臂,
当阻力及阻力臂不变时,动力动力臂为定值,且定值,
动力随着动力臂的增大而减小,
杠杆向下运动时的度数越来越小,此时的值越来越大,
又动力臂,
此时动力臂也越来越大,
此时的动力越来越小,
故选:A.
根据杠杆原理及的值随着的减小而增大结合反比例函数的增减性即可求得答案.
本题主要考查了杠杆原理以及锐角三角函数和反比例函数的增减性等知识;熟练掌握相关知识是解决本题的关键.
6.【答案】A
【解析】解:根据题意可得:船离海岸线的距离为米
故选:A.
在直角三角形中,已知角的对边求邻边,可以用正切函数来解决.
本题考查解直角三角形的应用仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
7.【答案】C
【解析】解:连结AE,
间的距离调节到60cm,木制活动衣帽架是由三个全等的菱形构成,
,
菱形的边长,
,
,
是等边三角形,
,
.
故选:C.
连结AE,根据全等的性质可得,根据菱形的性质和等边三角形的判定可得是等边三角形,再根据等边三角形和菱形的性质即可求解.
考查了菱形的性质,全等图形,等边三角形的判定与性质,解题的关键是得到是等边三角形.
8.【答案】C
【解析】解:,,,
,
,
米,
米,
故选:C.
首先证明米,解直角三角形求出BC即可.
本题考查解直角三角形的应用,等腰三角形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
9.【答案】B
【解析】解:在中,
,,
,
,
,
即河宽米,
故选:B.
在直角三角形PQT中,利用PQ的长,以及的度数,进而得到的度数,根据三角函数即可求得PT的长.
此题考查了解直角三角形的应用方向角问题,掌握方向角与正切函数的定义是解题的关键.
10.【答案】C
【解析】解:如图,过点A作于点F,
根据题意可知:
,,
四边形ABEF是矩形,
,,
在中,,
,
在中,,
,
,
解得,
.
答:乙楼的高度CE为.
故选:C.
过点A作于点F,根据题意可得,四边形ABEF是矩形,再根据特殊角三角函数即可求出乙楼的高度.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
11.【答案】500
【解析】解:在中,
米,,
米.
故答案为:500.
根据题意,从B点跑至A点,实际下降的高度为BC,在中,求出BC的长度即可.
本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数的知识求解.
12.【答案】64
【解析】解:如图,连接AB,CD,过点A作于E,过点B作于F.
,,
四边形ABFE是平行四边形,
,
四边形AEFB是矩形,
,
,
,
,
同法可得,
,
故答案为64.
如图,连接AB,CD,过点A作于E,过点B作于求出CE,EF,DF即可解决问题.
本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线面构造直角三角形解决问题.
13.【答案】328
【解析】解:如图,在中,,,
,
在中,,
,
答:该建筑物的高度BC约为328米.
故答案为:328.
在中,根据正切函数求得,在中,求得,再根据,代入数据计算即可.
此题考查了解直角三角形的应用仰角俯角问题.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.
14.【答案】
【解析】解:由题意可得:,,
则在直角中,
,
故这个坡面的坡度为:.
故答案为:.
直接利用勾股定理得出AC的长,再利用坡角的定义得出答案.
此题主要考查了坡角的定义,正确把握坡角的定义是解题关键.
15.【答案】解:,,
,
,
四边形CDNM是矩形,
,,
在中,,
,
在中,,
,
,
,
,,
在中,,
,
米.
【解析】根据平行线的判定定理得到,推出四边形CDNM是矩形,根据矩形的性质得到,,解直角三角形即可得到结论.
本题考查了解直角三角形仰角俯角问题,矩形的判定和性质,正确的识别图形是解题的关键.
16.【答案】解:延长ED交AB于H,延长MQ交BA的延长线于T.
由题意,,
,
四边形BCDH是矩形,
,
,
,
,
,
,
.
【解析】延长ED交AB于H,延长MQ交BA的延长线于利用平行线分线段成比例定理解决问题即可.
本题考查解直角三角形的应用,平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.
17.【答案】解:过A作交CD的延长线于E,
则,
在中,,
,
,
在中,,
,
,
,
答:办公楼的高CD为
【解析】过A作交CD的延长线于E,在和中,由三角函数定义求出DE、CE的长,即可解决问题.
本题考查了解直角三角形的应用仰角俯角问题;解题的关键是借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.
第2页,共2页
第1页,共1页
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
