人教版八年级数学上册同步练习题 : 13.4 课题学习--最短路径问题(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册同步练习题 : 13.4 课题学习--最短路径问题(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 281.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 00:00:00 | ||
图片预览


文档简介
人教版八年级数学上册同步练习题
第十三章轴对称
13.4
课题学习--最短路径问题
一、单选题
1.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.点A
B.点B
C.AB之间
D.BC之间
2.已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为(
)
A.(
,-4)
B.(
,0)
C.(
,0)
D.(
,0)
3.平面直角坐标系xOy中,已知A(-1,0),B(3,0),C(0,-1)三点,D(1,m)是一个动点,当△ACD的周长最小时,则△ABD的面积为(
)
A.
B.
C.
D.
4.x是数轴上任意一点表示的数,若|x﹣3|+|x+2|的值最小,则x的取值范围是(
)
A.x≥3
B.x≤﹣2
C.﹣2≤x≤3
D.﹣2<x<3
5.如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是(
)
A.2
B.4
C.6
D.8
6.如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(
)
A.①②
B.②③
C.①③
D.①④
7.如图,中,,,,,是的平分线.若P、Q分别是和上的动点,则的最小值是(
)
A.
B.4
C.
D.5
8.如图,在矩形中,,将矩形沿折叠,使点与点重合,则折痕的长为(
)
A.6
B.12
C.
D.
9.A,B,C三个车站在东西方向笔直的一条公路上,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在( )
A.在A的左侧
B.在AB之间
C.在BC之间
D.B处
10.A、B是直线l上的两点,P是直线l上的任意一点,要使PA+PB的值最小,那么点P的位置应在( )
A.线段AB上
B.线段AB的延长线上
C.线段AB的反向延长线上
D.直线l上
二、填空题
11.如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4,E是AB边的中点,F是AC边的中点,则(1)EF=____;(2)若D是BC边上一动点,则△EFD的周长最小值是____.
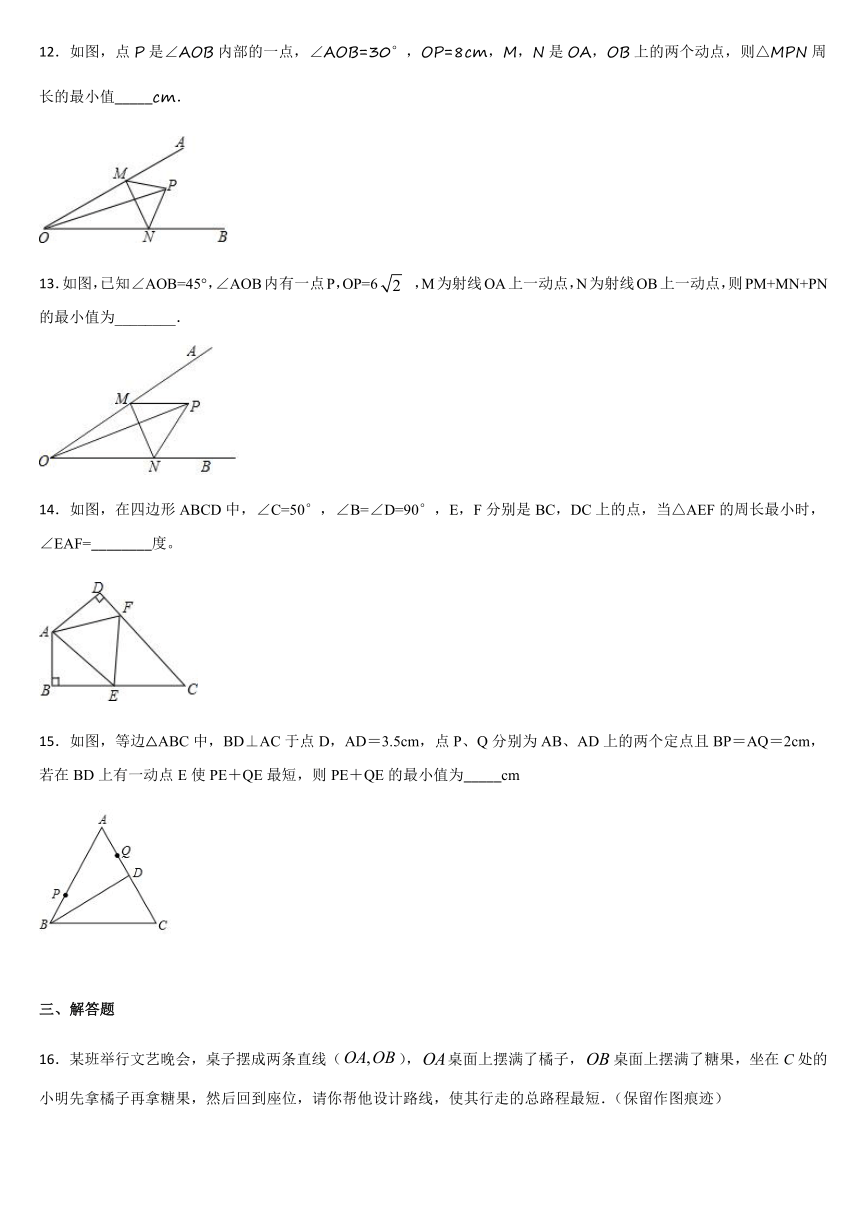
12.如图,点P是∠AOB内部的一点,∠AOB=30°,OP=8cm,M,N是OA,OB上的两个动点,则△MPN周长的最小值_____cm.
13.如图,已知∠AOB=45°,∠AOB内有一点P,OP=6
,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为________.
14.如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF=________度。
15.如图,等边△ABC中,BD⊥AC于点D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE最短,则PE+QE的最小值为_____cm
三、解答题
16.某班举行文艺晚会,桌子摆成两条直线(),桌面上摆满了橘子,桌面上摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮他设计路线,使其行走的总路程最短.(保留作图痕迹)
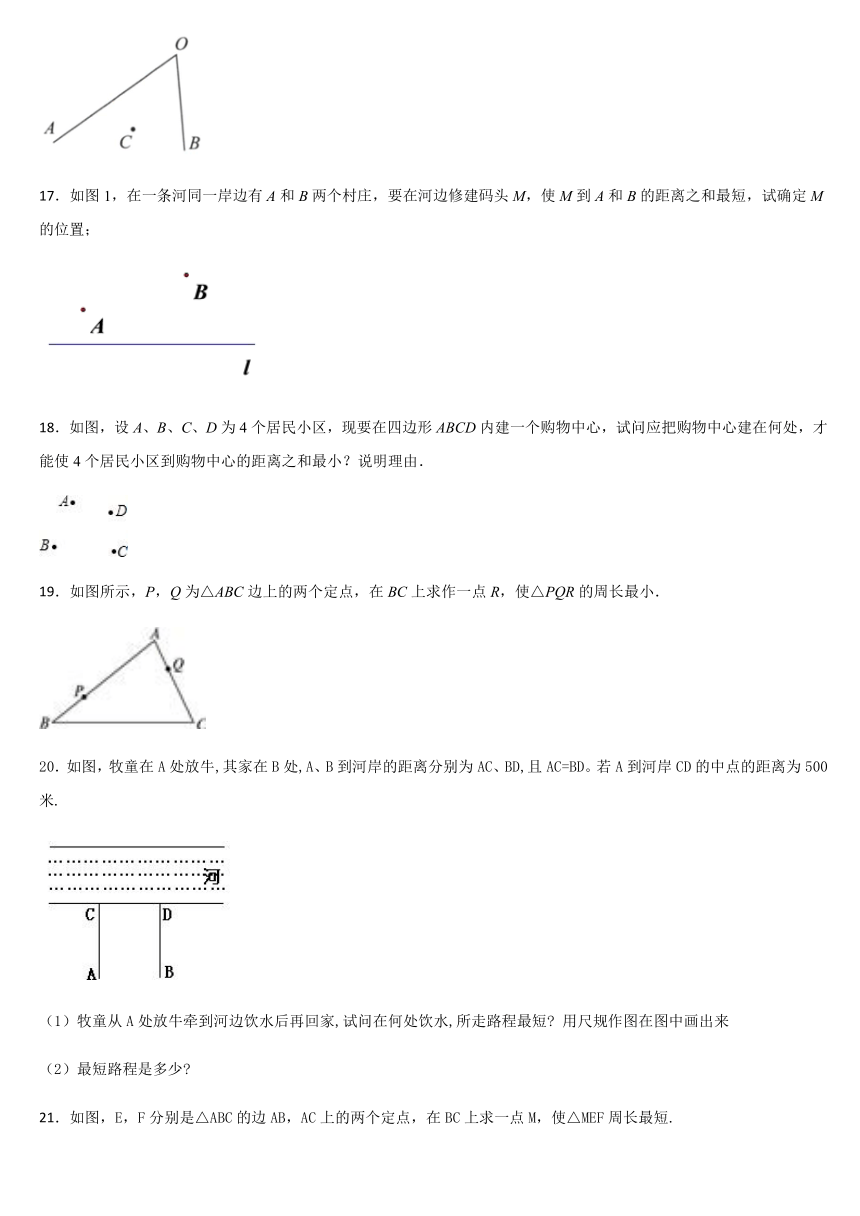
17.如图1,在一条河同一岸边有A和B两个村庄,要在河边修建码头M,使M到A和B的距离之和最短,试确定M的位置;
18.如图,设A、B、C、D为4个居民小区,现要在四边形ABCD内建一个购物中心,试问应把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?说明理由.
19.如图所示,P,Q为△ABC边上的两个定点,在BC上求作一点R,使△PQR的周长最小.
20.如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD。若A到河岸CD的中点的距离为500米.
(1)牧童从A处放牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?
用尺规作图在图中画出来
(2)最短路程是多少?
21.如图,E,F分别是△ABC的边AB,AC上的两个定点,在BC上求一点M,使△MEF周长最短.
22.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,求∠AMN+∠ANM的度数.
23.如图所示的是某风景区的旅游路线示意图,其中B,C,D为风景点,E为两条路的交叉点,图中数据为两相应点间的距离(单位:千米).一位游客从A处出发,以2千米/时的速度步行游览,每个景点的逗留时间均为小时.
(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了4小时,求CE的长;
(2)若此学生打算从A处出发,步行速度与景点的逗留时间保持不变,且在最短时间内看完三个景点返回到A处,请你为他设计一条步行路线,说明这样设计的理由
【参考答案】
1.A
2.C
3.C
4.C
5.B
6.D
7.C
8.D
9.D
10.A
11.2
2+2
12.8
13.12
14.80°
15.5
16.如图所示,小明的行走路线为,此时所走的总路程为的长,总路程最短.
17.所求点如下图所示:
∵两点之间线段最短,
∴需要能将AM、BM两边转化到一条直线上,
∴用轴对称可以办到,
求点M的位置的具体步骤如下:
①作作点A关于直线BC的轴对称点A’,
②连结A’B交BC于点M,
③连结AM,
则点M就是所求作的点,能够使M到A和B的距离之和最短.
18.应建在AC、BD连线的交点处.
理由:根据两点之间线段最短,将A、C,B、D用线段连起来,路程最短,
两线段的交点处建购物中心则使4个居民小区到购物中心的距离之和最小.
19.(1)作点P关于BC所在直线的对称点P′,
(2)连接P′Q,交BC于点R,则点R就是所求作的点(如图所示).
20.(1)作出A的对称点A′,连接A′B与CD相交于M,则牧童从A处把牛牵到河边饮水再回家,最短距离是A′B的长.
(2)易得△A′CM≌△BDM,AC=BD,
所以A′C=BD,
则
,
所以CM=DM,M为CD的中点,
由于A到河岸CD的中点的距离为500米,
所以A′到M的距离为500米,
A′B=1000米.
故最短距离是1000米.
21.作关于的对称点,连结交于
则周长最短,如图所示:
22.作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,连接AM,AN,则A′A″即为△AMN的周长最小值.作DA延长线AH.
∵∠DAB=120°,
∴∠HAA′=60°.
∴∠A′+∠A″=∠HAA′=60°.
∵∠A′=∠MAA′,∠NAD=∠A″,且∠A′+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAD+∠A″=2(∠A′+∠A″)=2×60°=120°.
23.(1)设CE长为x千米,则2.2+1.4+x+1.2=2×(4-2×0.75),解得:x=0.2(千米).
(2)若步行路线为A→D→C→B→E→A(或A→E→B→C→D→A),则所用时间为:
(2.2+1.4+2+0.6+1.2)÷2+3×0.75=5.95(小时).
若步行路线为A→D→C→E→B→E→A(或A→E→B→E→C→D→A),则所用时间为:
(2.2+1.4+0.2+0.6×2+1.2)÷2+3×0.75=5.35(小时).
因为5.95>5.35,所以步行路线应为A→D→C→E→B→E→A(或A→E→B→E→C→D→A).
第十三章轴对称
13.4
课题学习--最短路径问题
一、单选题
1.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.点A
B.点B
C.AB之间
D.BC之间
2.已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为(
)
A.(
,-4)
B.(
,0)
C.(
,0)
D.(
,0)
3.平面直角坐标系xOy中,已知A(-1,0),B(3,0),C(0,-1)三点,D(1,m)是一个动点,当△ACD的周长最小时,则△ABD的面积为(
)
A.
B.
C.
D.
4.x是数轴上任意一点表示的数,若|x﹣3|+|x+2|的值最小,则x的取值范围是(
)
A.x≥3
B.x≤﹣2
C.﹣2≤x≤3
D.﹣2<x<3
5.如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是(
)
A.2
B.4
C.6
D.8
6.如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(
)
A.①②
B.②③
C.①③
D.①④
7.如图,中,,,,,是的平分线.若P、Q分别是和上的动点,则的最小值是(
)
A.
B.4
C.
D.5
8.如图,在矩形中,,将矩形沿折叠,使点与点重合,则折痕的长为(
)
A.6
B.12
C.
D.
9.A,B,C三个车站在东西方向笔直的一条公路上,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在( )
A.在A的左侧
B.在AB之间
C.在BC之间
D.B处
10.A、B是直线l上的两点,P是直线l上的任意一点,要使PA+PB的值最小,那么点P的位置应在( )
A.线段AB上
B.线段AB的延长线上
C.线段AB的反向延长线上
D.直线l上
二、填空题
11.如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4,E是AB边的中点,F是AC边的中点,则(1)EF=____;(2)若D是BC边上一动点,则△EFD的周长最小值是____.
12.如图,点P是∠AOB内部的一点,∠AOB=30°,OP=8cm,M,N是OA,OB上的两个动点,则△MPN周长的最小值_____cm.
13.如图,已知∠AOB=45°,∠AOB内有一点P,OP=6
,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为________.
14.如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF=________度。
15.如图,等边△ABC中,BD⊥AC于点D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE最短,则PE+QE的最小值为_____cm
三、解答题
16.某班举行文艺晚会,桌子摆成两条直线(),桌面上摆满了橘子,桌面上摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮他设计路线,使其行走的总路程最短.(保留作图痕迹)
17.如图1,在一条河同一岸边有A和B两个村庄,要在河边修建码头M,使M到A和B的距离之和最短,试确定M的位置;
18.如图,设A、B、C、D为4个居民小区,现要在四边形ABCD内建一个购物中心,试问应把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?说明理由.
19.如图所示,P,Q为△ABC边上的两个定点,在BC上求作一点R,使△PQR的周长最小.
20.如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD。若A到河岸CD的中点的距离为500米.
(1)牧童从A处放牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?
用尺规作图在图中画出来
(2)最短路程是多少?
21.如图,E,F分别是△ABC的边AB,AC上的两个定点,在BC上求一点M,使△MEF周长最短.
22.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,求∠AMN+∠ANM的度数.
23.如图所示的是某风景区的旅游路线示意图,其中B,C,D为风景点,E为两条路的交叉点,图中数据为两相应点间的距离(单位:千米).一位游客从A处出发,以2千米/时的速度步行游览,每个景点的逗留时间均为小时.
(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了4小时,求CE的长;
(2)若此学生打算从A处出发,步行速度与景点的逗留时间保持不变,且在最短时间内看完三个景点返回到A处,请你为他设计一条步行路线,说明这样设计的理由
【参考答案】
1.A
2.C
3.C
4.C
5.B
6.D
7.C
8.D
9.D
10.A
11.2
2+2
12.8
13.12
14.80°
15.5
16.如图所示,小明的行走路线为,此时所走的总路程为的长,总路程最短.
17.所求点如下图所示:
∵两点之间线段最短,
∴需要能将AM、BM两边转化到一条直线上,
∴用轴对称可以办到,
求点M的位置的具体步骤如下:
①作作点A关于直线BC的轴对称点A’,
②连结A’B交BC于点M,
③连结AM,
则点M就是所求作的点,能够使M到A和B的距离之和最短.
18.应建在AC、BD连线的交点处.
理由:根据两点之间线段最短,将A、C,B、D用线段连起来,路程最短,
两线段的交点处建购物中心则使4个居民小区到购物中心的距离之和最小.
19.(1)作点P关于BC所在直线的对称点P′,
(2)连接P′Q,交BC于点R,则点R就是所求作的点(如图所示).
20.(1)作出A的对称点A′,连接A′B与CD相交于M,则牧童从A处把牛牵到河边饮水再回家,最短距离是A′B的长.
(2)易得△A′CM≌△BDM,AC=BD,
所以A′C=BD,
则
,
所以CM=DM,M为CD的中点,
由于A到河岸CD的中点的距离为500米,
所以A′到M的距离为500米,
A′B=1000米.
故最短距离是1000米.
21.作关于的对称点,连结交于
则周长最短,如图所示:
22.作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,连接AM,AN,则A′A″即为△AMN的周长最小值.作DA延长线AH.
∵∠DAB=120°,
∴∠HAA′=60°.
∴∠A′+∠A″=∠HAA′=60°.
∵∠A′=∠MAA′,∠NAD=∠A″,且∠A′+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAD+∠A″=2(∠A′+∠A″)=2×60°=120°.
23.(1)设CE长为x千米,则2.2+1.4+x+1.2=2×(4-2×0.75),解得:x=0.2(千米).
(2)若步行路线为A→D→C→B→E→A(或A→E→B→C→D→A),则所用时间为:
(2.2+1.4+2+0.6+1.2)÷2+3×0.75=5.95(小时).
若步行路线为A→D→C→E→B→E→A(或A→E→B→E→C→D→A),则所用时间为:
(2.2+1.4+0.2+0.6×2+1.2)÷2+3×0.75=5.35(小时).
因为5.95>5.35,所以步行路线应为A→D→C→E→B→E→A(或A→E→B→E→C→D→A).
