华东师大版八年级上册 数学 课件: 13.2.2全等三角形的判定条件(31张PPT)
文档属性
| 名称 | 华东师大版八年级上册 数学 课件: 13.2.2全等三角形的判定条件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 716.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 00:00:00 | ||
图片预览



文档简介
(共31张PPT)
全等三角形的判定条件
A
B
C
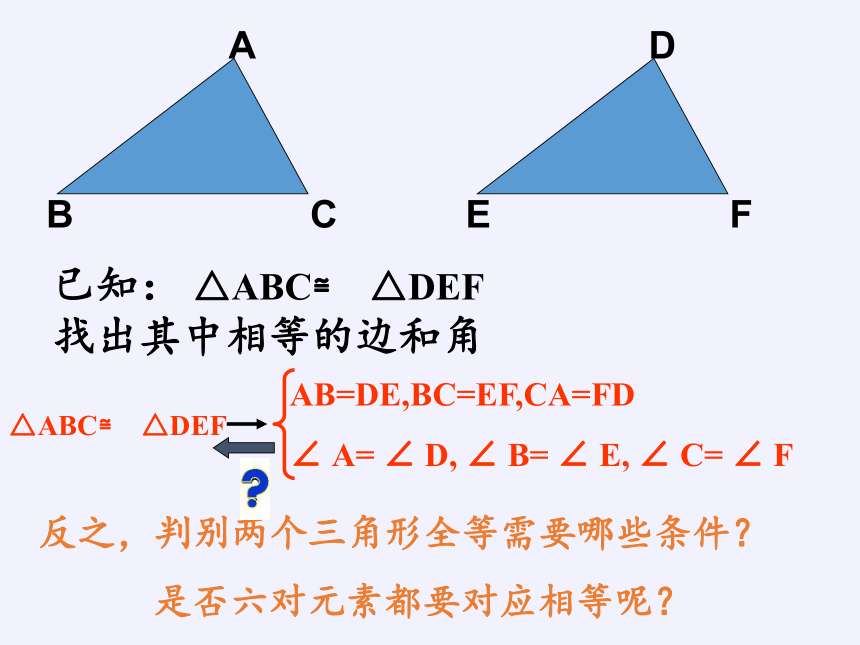
已知:
△ABC≌
△DEF
找出其中相等的边和角
反之,判别两个三角形全等需要哪些条件?
是否六对元素都要对应相等呢?
D
E
F
AB=DE,BC=EF,CA=FD
∠
A=
∠
D,
∠
B=
∠
E,
∠
C=
∠
F
△ABC≌
△DEF
一个条件
不能判定三角形全等
寻求判别三角形全等的条件
三个条件
边边边
角角角
两角一边
两边一角
两个条件
全等三角形:三组边相等,三对角相等
一组边相等
一对角相等
不能判定三角形全等
两边和它的夹角
两边和它一边的对角
两角和它的夹边
两角和一角的对边
一边一角相等
两对角相等
两组边相等
已知一个三角形的三个内角分别为40o,60o,80o,你能画出这个三角形吗?与同学比较,它们全等吗?
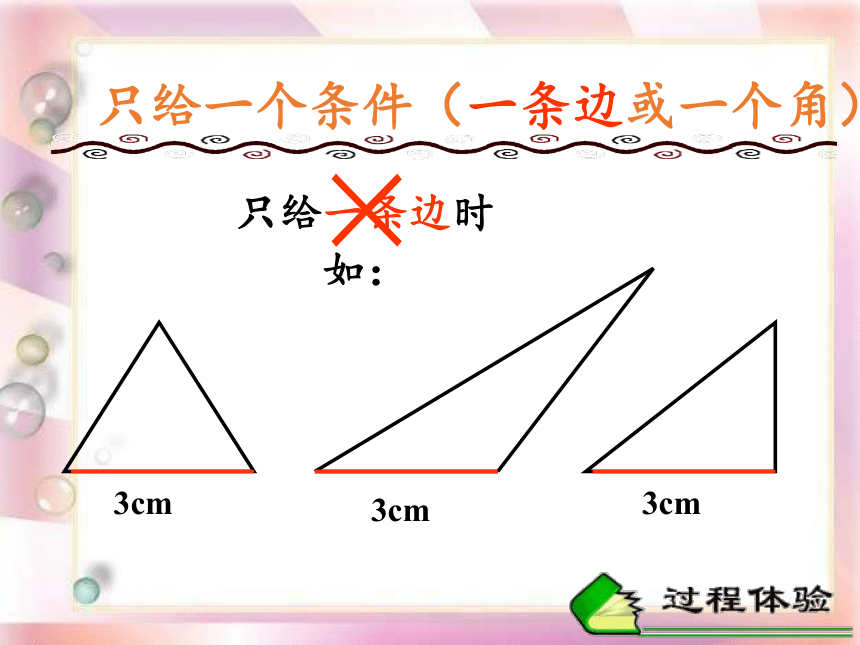
只给一个条件(一条边或一个角)
只给一条边时
如:
3cm
3cm
3cm
×
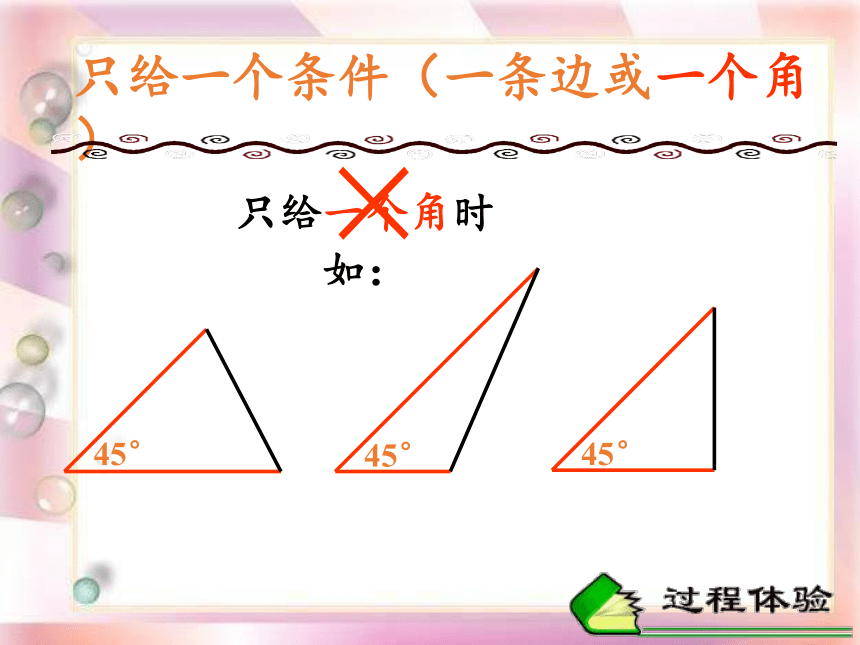
只给一个角时
如:
45°
45°
45°
只给一个条件(一条边或一个角)
×
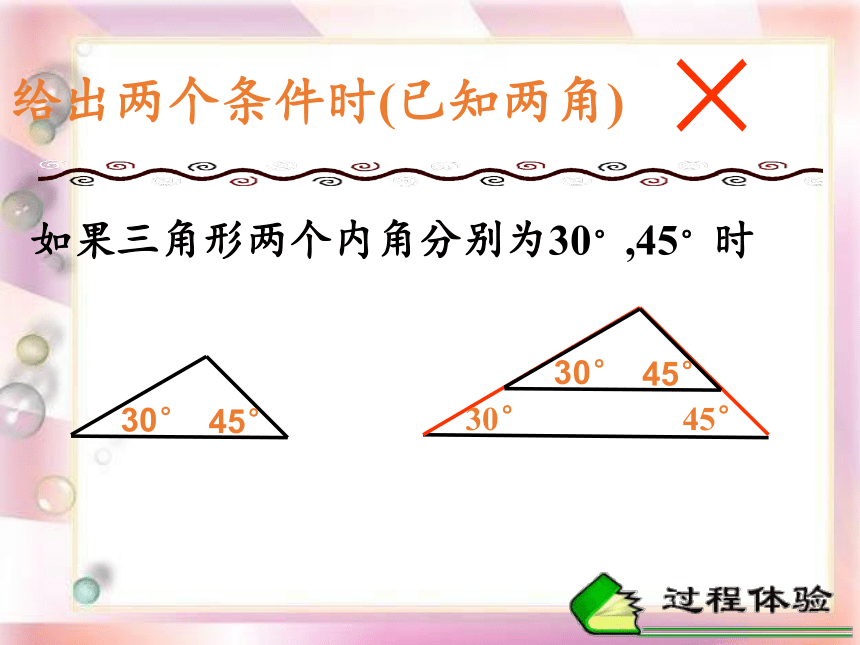
给出两个条件时(已知两角)
如果三角形两个内角分别为30°,45°时
30°
45°
30°
45°
30°
45°
×
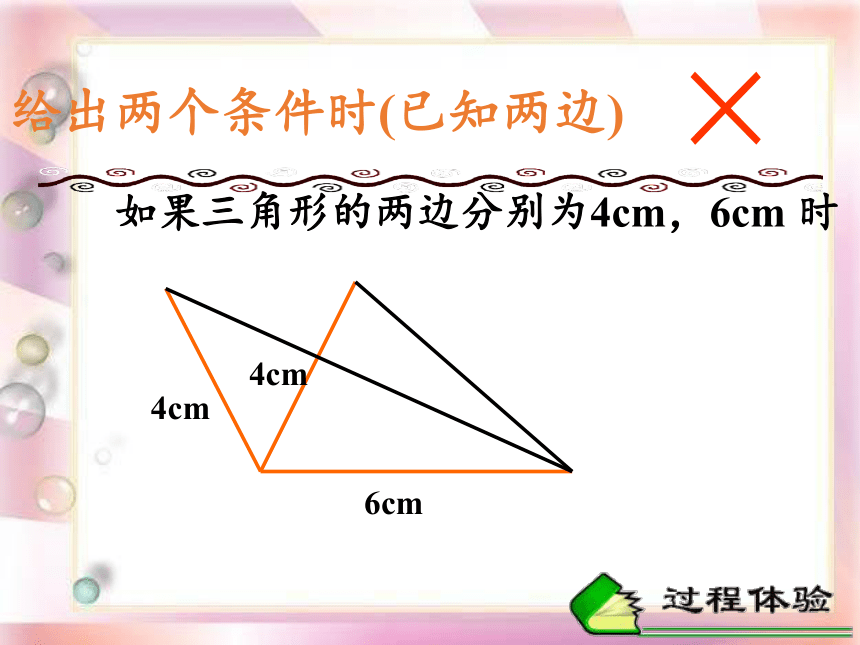
给出两个条件时(已知两边)
如果三角形的两边分别为4cm,6cm
时
6cm
4cm
4cm
×
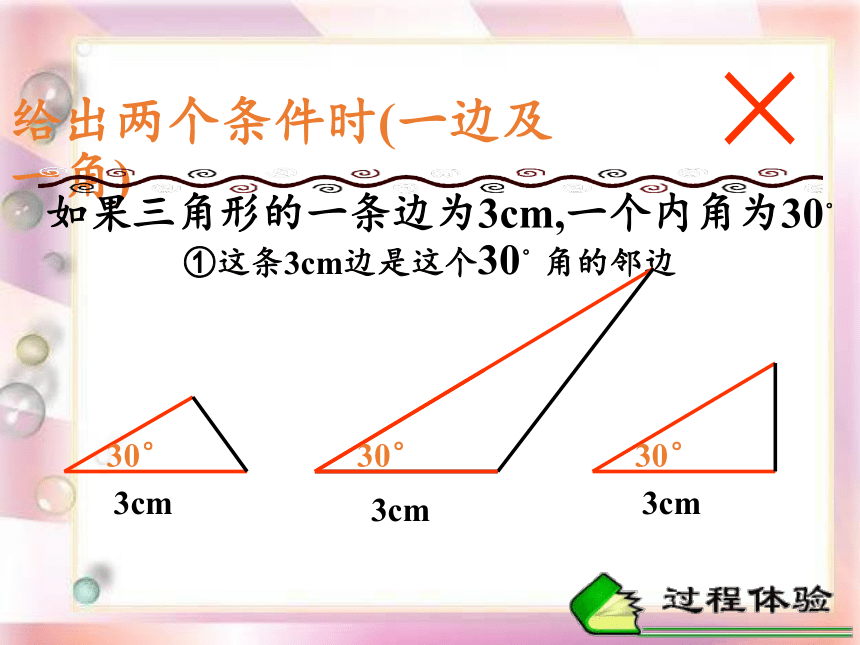
给出两个条件时(一边及一角)
如果三角形的一条边为3cm,一个内角为30°
①这条3cm边是这个30°角的邻边
3cm
3cm
3cm
30°
30°
30°
×
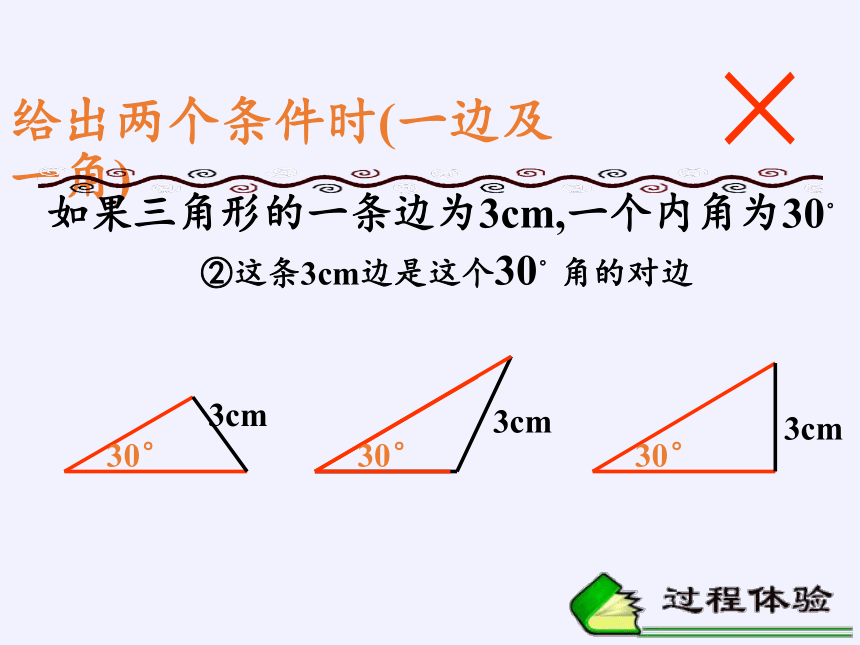
给出两个条件时(一边及一角)
如果三角形的一条边为3cm,一个内角为30°
②这条3cm边是这个30°角的对边
3cm
3cm
3cm
30°
30°
30°
×
一个条件
不能判定三角形全等
寻求判别三角形全等的条件
两个条件
全等三角形:三组边相等,三对角相等
一组边相等
一对角相等
不能判定三角形全等
一边一角相等
两对角相等
两组边相等
如果两个三角形有三组对应相等的元素(边或角),那么会有几种可能的情况?请列举出来。
13.2探索三角形全等的条件
两边一角对应相等
两边夹角对应相等
(边角边)
两边一对角对应相等
(边边角)
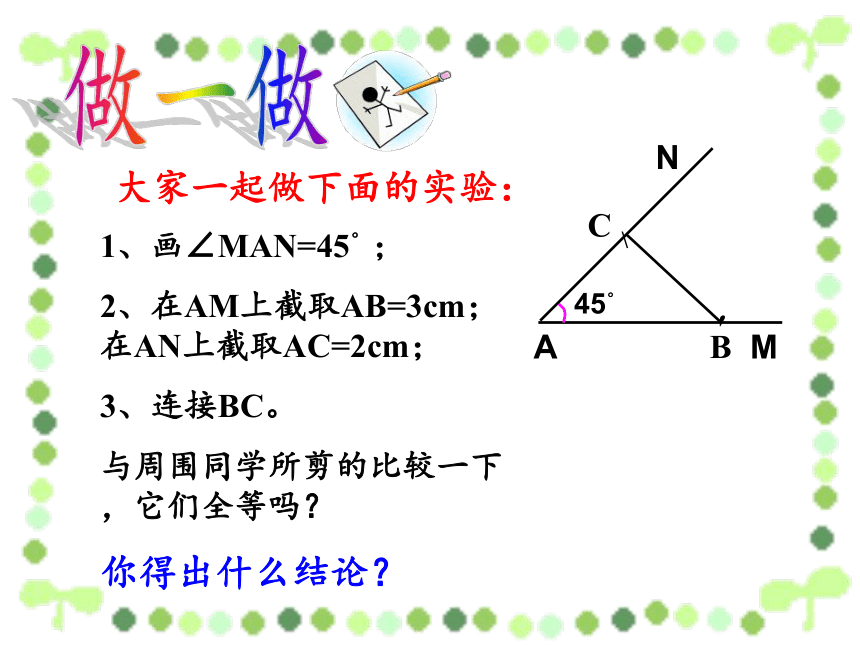
大家一起做下面的实验:
1、画∠MAN=45°;
2、在AM上截取AB=3cm;在AN上截取AC=2cm;
3、连接BC。
与周围同学所剪的比较一下,它们全等吗?
你得出什么结论?
B
C
A
M
N
45°
′
\
做一做
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
\\
\
A
B
C
\\
\
D
E
F
在△ABC和△
DEF中,
AB=DE
∠B=∠E
BC=EF
∴
△ABC≌△DEF
(SAS)
若两个三角形两边以及这两边的夹角对应相等
则这两个三角形全等
条件:
AB=DE,
∠B=∠E,
BC=EF
结论:
△ABC≌△DEF
11.3探索三角形全等的条件(1.2)
两边一角对应相等
两边夹角对应相等
(边角边)
两边一对角对应相等
(边边角)
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
\\
\
A
B
C
\\
\
D
E
F
在△ABC和△
DEF中,
AB=DE
∠B=∠E
BC=EF
∴
△ABC≌△DEF
(SAS)
写出在哪两个三角形中证明全等。
按边、角、边的顺序列出三个条件,
用大括号合在一起.
写出结论.每步要有推理的依据
证明三角形全等的步骤:
?1.写出在哪两个三角形中证明全等。(注意把表示对应顶点的字母写在对应的位置上).
?2.按边、角、边的顺序列出三个条件,用大括号合在一起.
?3.写出结论.每步要有推理的依据.
P141练一练1:
在下列三角形中,哪两个三角形全等?
40°
4
4
30°
4
4
4
5
30°
4
5
30°
4
6
40°
4
6
40°
⑴
⑵
⑶
⑷
⑸
⑹
解:全等的三角形有:⑴和⑷,
⑶和⑸.
两边以及其中一边的对角对应相等的两个三角形全等吗?
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,
你发现了什么?
做一做
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其中一边所对的角对应相等,两个三角形不一定全等.
先画一个40°的角,然后在其中一边上取3.5厘米,最后画40°的角所对的边2.5厘米.
两边一角对应相等
两边夹角对应相等
(边角边)
两边一对角对应相等
(边边角)
×
√
再次明确
已知:如图,
AB=CB
,∠ABD=
∠CBD
△ABD
和△CBD
全等吗?
例1
分析:
△
ABD
≌△
CBD
边:
角:
边:
AB=CB
(已知)
∠ABD=∠CBD
(已知)
?
A
B
C
D
(SAS)
现在例1的已知条件不改变,而问题改变成:
问:AD与CD相等吗,BD平分∠ADC吗?
已知:如图,AB=CB,∠ABD=∠CBD
.
问:
AD与CD相等吗?
BD
平分∠
ADC
吗?
例题推广
A
B
C
D
归纳:判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
例2
如图,已知AD=AE,BE=CD,∠ADE=∠AED,△ADB与△AEC全等吗?请说明理由。
如图:MP=MQ,MN=MG,
∠
PMN=
∠
QMG.
请在图中找出全等三角形。并说明理由。
例3
A
B
C
D
O
1.
如图,AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
注意:
要充分利用图形中“对顶角相等”这个条件.
练一练:
2、如图:AB=AC,AD=AE,△ABE和△ACD全等吗?请说明理由。
A
E
D
C
B
练一练:
注意:
要充分利用图形中“公共角”这个条件.
你还能得到哪些相等的线段?说明理由.
A
E
D
B
C
3.已知:如图,AB=AC,AD=AE,不用量角器量,能得出∠B=∠C吗?请说明理由
练一练:
这节课你学到了什么?
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
两边以及其中一边的对角对应相等的两个三角形不一定全等.
注意:要充分利用图形中“对顶角相等,公共角”这些条件.
判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
课堂感悟
作业
评价手册:P79~81
第1课时2、3
本子
书P151~152:1
书P151~152:4(写在书上)
2.
如图,AC=BD,∠CAB=
∠DBA,你能判断BC=AD吗?说明理由。
A
B
C
D
谢
谢
全等三角形的判定条件
A
B
C
已知:
△ABC≌
△DEF
找出其中相等的边和角
反之,判别两个三角形全等需要哪些条件?
是否六对元素都要对应相等呢?
D
E
F
AB=DE,BC=EF,CA=FD
∠
A=
∠
D,
∠
B=
∠
E,
∠
C=
∠
F
△ABC≌
△DEF
一个条件
不能判定三角形全等
寻求判别三角形全等的条件
三个条件
边边边
角角角
两角一边
两边一角
两个条件
全等三角形:三组边相等,三对角相等
一组边相等
一对角相等
不能判定三角形全等
两边和它的夹角
两边和它一边的对角
两角和它的夹边
两角和一角的对边
一边一角相等
两对角相等
两组边相等
已知一个三角形的三个内角分别为40o,60o,80o,你能画出这个三角形吗?与同学比较,它们全等吗?
只给一个条件(一条边或一个角)
只给一条边时
如:
3cm
3cm
3cm
×
只给一个角时
如:
45°
45°
45°
只给一个条件(一条边或一个角)
×
给出两个条件时(已知两角)
如果三角形两个内角分别为30°,45°时
30°
45°
30°
45°
30°
45°
×
给出两个条件时(已知两边)
如果三角形的两边分别为4cm,6cm
时
6cm
4cm
4cm
×
给出两个条件时(一边及一角)
如果三角形的一条边为3cm,一个内角为30°
①这条3cm边是这个30°角的邻边
3cm
3cm
3cm
30°
30°
30°
×
给出两个条件时(一边及一角)
如果三角形的一条边为3cm,一个内角为30°
②这条3cm边是这个30°角的对边
3cm
3cm
3cm
30°
30°
30°
×
一个条件
不能判定三角形全等
寻求判别三角形全等的条件
两个条件
全等三角形:三组边相等,三对角相等
一组边相等
一对角相等
不能判定三角形全等
一边一角相等
两对角相等
两组边相等
如果两个三角形有三组对应相等的元素(边或角),那么会有几种可能的情况?请列举出来。
13.2探索三角形全等的条件
两边一角对应相等
两边夹角对应相等
(边角边)
两边一对角对应相等
(边边角)
大家一起做下面的实验:
1、画∠MAN=45°;
2、在AM上截取AB=3cm;在AN上截取AC=2cm;
3、连接BC。
与周围同学所剪的比较一下,它们全等吗?
你得出什么结论?
B
C
A
M
N
45°
′
\
做一做
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
\\
\
A
B
C
\\
\
D
E
F
在△ABC和△
DEF中,
AB=DE
∠B=∠E
BC=EF
∴
△ABC≌△DEF
(SAS)
若两个三角形两边以及这两边的夹角对应相等
则这两个三角形全等
条件:
AB=DE,
∠B=∠E,
BC=EF
结论:
△ABC≌△DEF
11.3探索三角形全等的条件(1.2)
两边一角对应相等
两边夹角对应相等
(边角边)
两边一对角对应相等
(边边角)
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
\\
\
A
B
C
\\
\
D
E
F
在△ABC和△
DEF中,
AB=DE
∠B=∠E
BC=EF
∴
△ABC≌△DEF
(SAS)
写出在哪两个三角形中证明全等。
按边、角、边的顺序列出三个条件,
用大括号合在一起.
写出结论.每步要有推理的依据
证明三角形全等的步骤:
?1.写出在哪两个三角形中证明全等。(注意把表示对应顶点的字母写在对应的位置上).
?2.按边、角、边的顺序列出三个条件,用大括号合在一起.
?3.写出结论.每步要有推理的依据.
P141练一练1:
在下列三角形中,哪两个三角形全等?
40°
4
4
30°
4
4
4
5
30°
4
5
30°
4
6
40°
4
6
40°
⑴
⑵
⑶
⑷
⑸
⑹
解:全等的三角形有:⑴和⑷,
⑶和⑸.
两边以及其中一边的对角对应相等的两个三角形全等吗?
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,
你发现了什么?
做一做
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其中一边所对的角对应相等,两个三角形不一定全等.
先画一个40°的角,然后在其中一边上取3.5厘米,最后画40°的角所对的边2.5厘米.
两边一角对应相等
两边夹角对应相等
(边角边)
两边一对角对应相等
(边边角)
×
√
再次明确
已知:如图,
AB=CB
,∠ABD=
∠CBD
△ABD
和△CBD
全等吗?
例1
分析:
△
ABD
≌△
CBD
边:
角:
边:
AB=CB
(已知)
∠ABD=∠CBD
(已知)
?
A
B
C
D
(SAS)
现在例1的已知条件不改变,而问题改变成:
问:AD与CD相等吗,BD平分∠ADC吗?
已知:如图,AB=CB,∠ABD=∠CBD
.
问:
AD与CD相等吗?
BD
平分∠
ADC
吗?
例题推广
A
B
C
D
归纳:判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
例2
如图,已知AD=AE,BE=CD,∠ADE=∠AED,△ADB与△AEC全等吗?请说明理由。
如图:MP=MQ,MN=MG,
∠
PMN=
∠
QMG.
请在图中找出全等三角形。并说明理由。
例3
A
B
C
D
O
1.
如图,AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
注意:
要充分利用图形中“对顶角相等”这个条件.
练一练:
2、如图:AB=AC,AD=AE,△ABE和△ACD全等吗?请说明理由。
A
E
D
C
B
练一练:
注意:
要充分利用图形中“公共角”这个条件.
你还能得到哪些相等的线段?说明理由.
A
E
D
B
C
3.已知:如图,AB=AC,AD=AE,不用量角器量,能得出∠B=∠C吗?请说明理由
练一练:
这节课你学到了什么?
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
两边以及其中一边的对角对应相等的两个三角形不一定全等.
注意:要充分利用图形中“对顶角相等,公共角”这些条件.
判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
课堂感悟
作业
评价手册:P79~81
第1课时2、3
本子
书P151~152:1
书P151~152:4(写在书上)
2.
如图,AC=BD,∠CAB=
∠DBA,你能判断BC=AD吗?说明理由。
A
B
C
D
谢
谢
