华东师大版九年级上册 数学 课件: 23.1.2平行线分线段成比例(21张PPT)
文档属性
| 名称 | 华东师大版九年级上册 数学 课件: 23.1.2平行线分线段成比例(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 522.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 14:57:05 | ||
图片预览






文档简介
(共21张PPT)
平行线分线段成比例
1.知识目标:
①了解平行线分线段成比例定理
②会用平行线分线段成比例定理解决
实际问题
2.能力目标:
掌握推理证明的方法,发展演绎推
理能力
学习目标:
四条线段
a、b、c、d
中,如果
a:b=c:d,那么这四条线段a、b、c、d
叫做成比例的线段,简称比例线段.
2.比例的基本性质
如果
a:b
=c:d
,那么ad
=bc.
如果
ad
=bc,那么
a:b
=c:d
.
1.比例线段的概念:
回顾复习
如图3-6中,小方格边长都为1,平行线l1
∥l2∥
l3.分别交直线m,n
。
(1)计算
的值,你有什么发现?
(2)将
向下平移到如图3-7的位置,直线m,n
与
的交点分别为
你在问题(1)中发现结论还成立吗?如果将
平移到其它位置呢?
图3-6
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
动-动-脑!
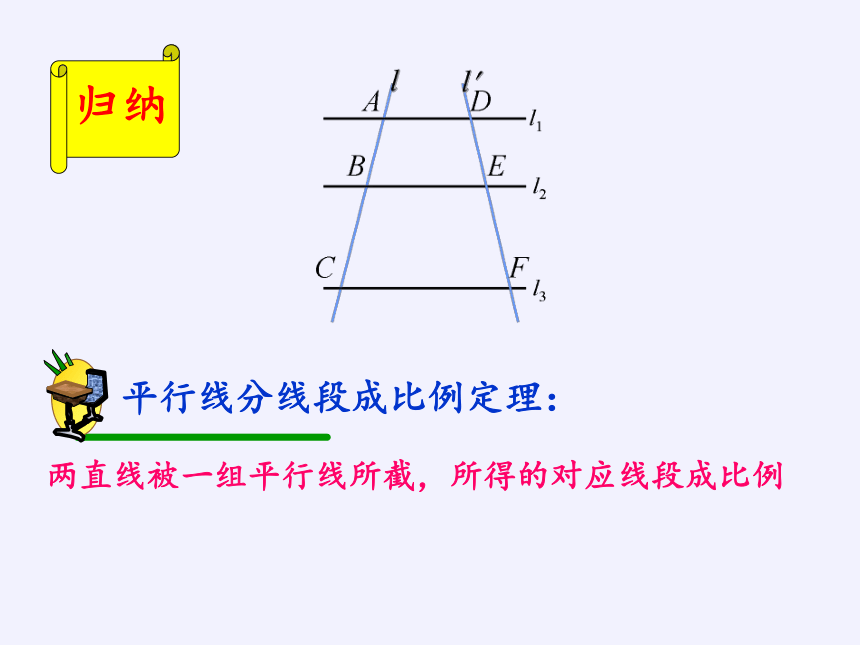
两直线被一组平行线所截,所得的对应线段成比例
归纳
平行线分线段成比例定理:
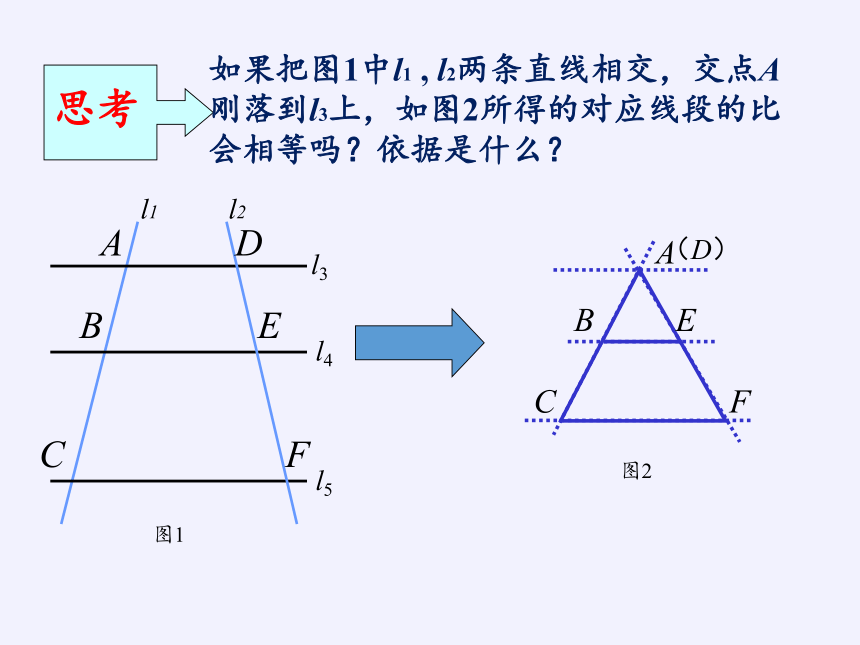
思考
如果把图1中l1
,
l2两条直线相交,交点A刚落到l3上,如图2所得的对应线段的比会相等吗?依据是什么?
A
B
C
E
F
图2
A
B
C
D
E
F
l3
l4
l5
l1
l2
(D)
图1
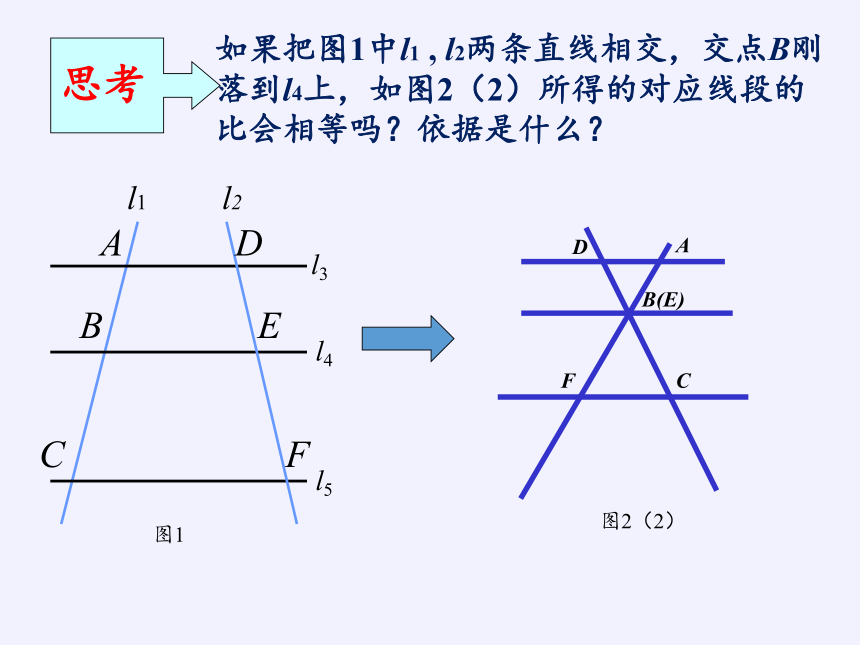
思考
如果把图1中l1
,
l2两条直线相交,交点B刚落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
A
B
C
D
E
F
l3
l4
l5
l1
l2
B(E)
F
C
D
A
图1
图2(2)
l2
l3
l1
l3
l
l?
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
推
论
1.已知:如图,在△ABC中,DE∥BC,以下结论正确的是( )
A.AE∶AC=AD∶BD
B.AE∶AC=BD∶AB
C.AE∶CE=AD∶BD
D.AC∶CE=AD∶BD
习题巩固
c
A
试一试
3.如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC。
(1)如果AE=7
,EB=5,FC=4.那么AF的长是多少?
(2)如果AB=10
,AE=6,AF=5.那么FC的长是多少?
A
B
C
E
F
4.如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB
DF∥AC,
EF∥BC
证明:
1、平行线分线段成比例定理:
(1)两直线被一组平行线所截,所得的对应线段成比例(关键要能熟练地找出对应线段)
(2)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
2、要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
课堂小结
3、注意该定理在三角形中的应用
习题巩固
2.如图,在△ABC中,DE∥BC,AC=4
,AB=3,EC=1.求AD和BD.
∴AE=3.
解∵AC=4,EC=1,
∵
DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
2.如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,
BC=8.求BF和CF的长.
F
A
C
B
分析:运用平行线分线段成比例定理的推论分别列出比例式求解.
解
∵DE//BC
∵DF//AC
D
E
拓展延伸
拓展延伸
.
(1)若AD1=
AB,AE1=
AC,则D1E1=
;
(2)若D1D2=
D1B,E1E2=
E1C,则D2E2=
;
D2B,E2E3=
E2C,则D3E3=
;……
(3)若D2D3=
Dn-1B,En-1En=
En-1C,则DnEn=
.
(4)若Dn-1Dn=
3.
如图,ΔABC中,BC=a.
习题23.1
作业布置
谢
谢
平行线分线段成比例
1.知识目标:
①了解平行线分线段成比例定理
②会用平行线分线段成比例定理解决
实际问题
2.能力目标:
掌握推理证明的方法,发展演绎推
理能力
学习目标:
四条线段
a、b、c、d
中,如果
a:b=c:d,那么这四条线段a、b、c、d
叫做成比例的线段,简称比例线段.
2.比例的基本性质
如果
a:b
=c:d
,那么ad
=bc.
如果
ad
=bc,那么
a:b
=c:d
.
1.比例线段的概念:
回顾复习
如图3-6中,小方格边长都为1,平行线l1
∥l2∥
l3.分别交直线m,n
。
(1)计算
的值,你有什么发现?
(2)将
向下平移到如图3-7的位置,直线m,n
与
的交点分别为
你在问题(1)中发现结论还成立吗?如果将
平移到其它位置呢?
图3-6
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
动-动-脑!
两直线被一组平行线所截,所得的对应线段成比例
归纳
平行线分线段成比例定理:
思考
如果把图1中l1
,
l2两条直线相交,交点A刚落到l3上,如图2所得的对应线段的比会相等吗?依据是什么?
A
B
C
E
F
图2
A
B
C
D
E
F
l3
l4
l5
l1
l2
(D)
图1
思考
如果把图1中l1
,
l2两条直线相交,交点B刚落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
A
B
C
D
E
F
l3
l4
l5
l1
l2
B(E)
F
C
D
A
图1
图2(2)
l2
l3
l1
l3
l
l?
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
推
论
1.已知:如图,在△ABC中,DE∥BC,以下结论正确的是( )
A.AE∶AC=AD∶BD
B.AE∶AC=BD∶AB
C.AE∶CE=AD∶BD
D.AC∶CE=AD∶BD
习题巩固
c
A
试一试
3.如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC。
(1)如果AE=7
,EB=5,FC=4.那么AF的长是多少?
(2)如果AB=10
,AE=6,AF=5.那么FC的长是多少?
A
B
C
E
F
4.如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB
DF∥AC,
EF∥BC
证明:
1、平行线分线段成比例定理:
(1)两直线被一组平行线所截,所得的对应线段成比例(关键要能熟练地找出对应线段)
(2)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
2、要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
课堂小结
3、注意该定理在三角形中的应用
习题巩固
2.如图,在△ABC中,DE∥BC,AC=4
,AB=3,EC=1.求AD和BD.
∴AE=3.
解∵AC=4,EC=1,
∵
DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
2.如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,
BC=8.求BF和CF的长.
F
A
C
B
分析:运用平行线分线段成比例定理的推论分别列出比例式求解.
解
∵DE//BC
∵DF//AC
D
E
拓展延伸
拓展延伸
.
(1)若AD1=
AB,AE1=
AC,则D1E1=
;
(2)若D1D2=
D1B,E1E2=
E1C,则D2E2=
;
D2B,E2E3=
E2C,则D3E3=
;……
(3)若D2D3=
Dn-1B,En-1En=
En-1C,则DnEn=
.
(4)若Dn-1Dn=
3.
如图,ΔABC中,BC=a.
习题23.1
作业布置
谢
谢
