华东师大版九年级上册22.3实践与探索3 变化率问题课件(共18张PPT)
文档属性
| 名称 | 华东师大版九年级上册22.3实践与探索3 变化率问题课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 373.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 16:39:10 | ||
图片预览





文档简介
(共20张PPT)
22.3实践与探索
3、变化率问题
华东师大版九年级上册
学而不疑则怠,疑而不探则空
知识链接
增加一倍,就是增加了100%;?翻一番,也是增加了100%。除了一倍与一番相当外,两倍与两番以上的数字含义就不同了。而且数字越大,差距越大。如增加两倍,就指增加200%;翻两番,就是400%(一番是二,二番是四,三番就是八),所以说翻两番就是增加了300%,翻三番就是增加了700%。“番”是按几何级数计算的(就是2的x次方),“倍”是按算术级数计算的。
翻番数与增长倍数
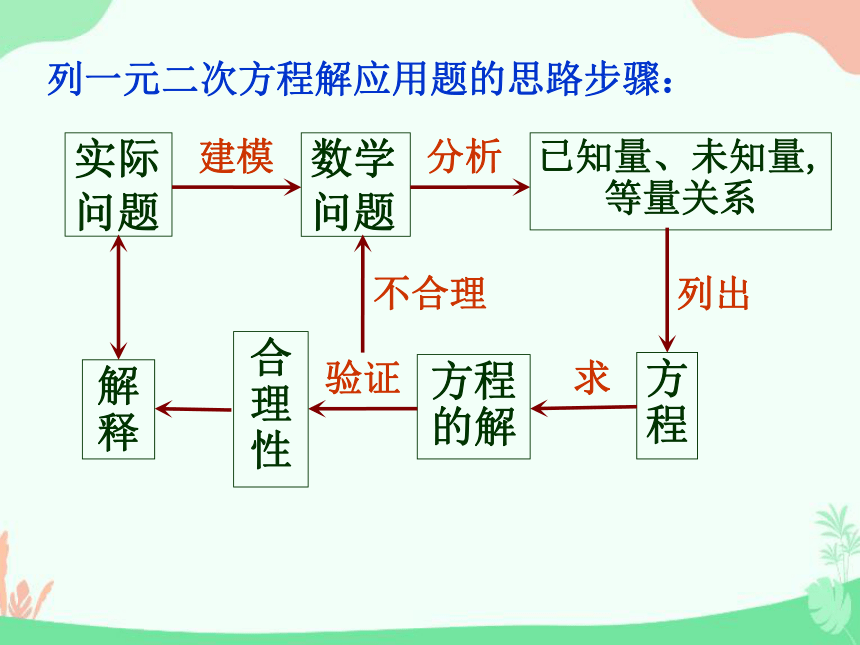
列一元二次方程解应用题的思路步骤:
实际
问题
建模
数学
问题
分析
已知量、未知量,等量关系
列出
方程
求
方程的解
验证
合理性
不合理
解释
探索求知
增长率问题:
若用a表示增长(降低)前的数据,x表示
增长率(降低率),b表示变化后的新量,
n表示连续变化的次数,则有公式为:
a(1+x)n=b或a(1-x)n=b
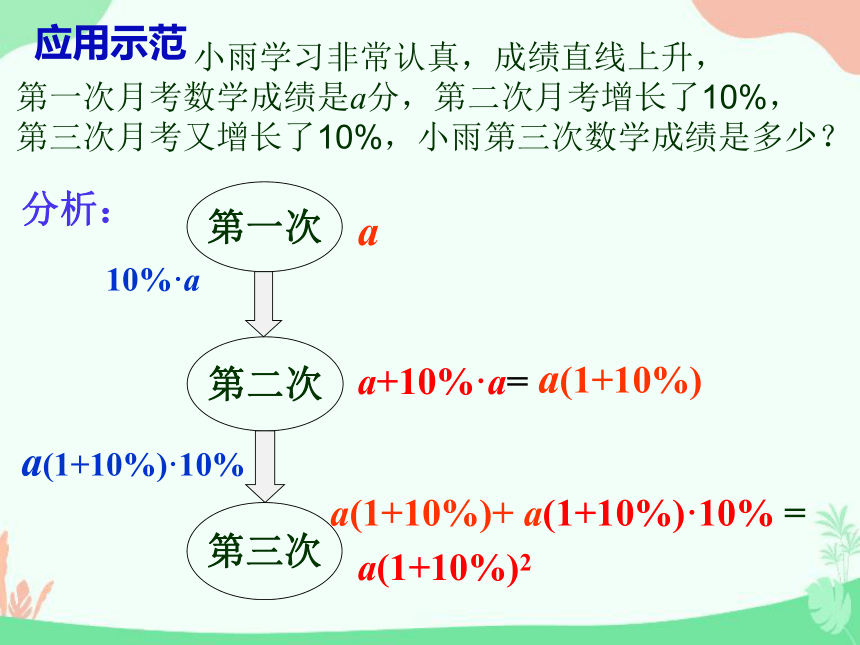
小雨学习非常认真,成绩直线上升,
第一次月考数学成绩是a分,第二次月考增长了10%,
第三次月考又增长了10%,小雨第三次数学成绩是多少?
分析:
第三次
第二次
第一次
a
10%·a
a+10%·a=
a(1+10%)·10%
a(1+10%)+
a(1+10%)·10%
=
a(1+10%)2
a(1+10%)
应用示范
1、天道村的水稻2018年平均每公顷产
8000kg,2020年平均每公顷产9680kg,
求该村水稻每公顷产量的年平均增长率。
例题解析
设该村水稻每公顷产量的年平均增长率为x
(2)根据题意,列出相应方程
解题步骤:
(3)解这个方程,得x1=0.1,x2=-2.1.
(1)用含x的代数式表示:
①2019年种的水稻平均每公顷的产量为
②2020年种的水稻平均每公顷的产量为
8000(1+x)kg
8000(1+x)2kg
8000(1+x)2=9680
(4)检验:x1=0.1,x2=-2.1均为原方程的解,
但x2=-1.1不符合题意,舍去.
(5)答:该村水稻每公顷产量的年平均增长率为10%.
2、西部某区县楼盘准备以每平方米6000元的
均价对外销售,由于新冠疫情的影响,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)大强准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米100元,试问哪种方案更优惠?
例题解析
分析:
设平均每次下调的百分率为x,那么下调一次后
的价格为(6000-6000x)元,即6000(1-x)元,
下调两次后的价格为[6000(1-x)-6000(1-x)·x]元,即6000(1-x)2元,
由题意得,经两次下调后的价格为4860元,
由此可列方程为6000(1-x)2=4860.
解:(1)设平均每次下调的百分率为x,
根据题意,得6000(1-x)2=4860,
解方程,得x1=0.1,x2=1.9(舍去),
故每次下调的百分率为10%.
(2)方案①可以优惠4860×100×(1-0.98)
=9720元;方案②可以优惠100×100
=10000元.所以方案②更优惠。
方法归纳
对于经过两次变化的增长率问题,如果设基数
为a,增长率为x,那么第一次增长后的量为
a+ax,即a(1+x);而a(1+x)又是第二次增长的
基数,增长两次后的量是a(1+x)+a(1+x)x,
即a(1+x)2;同样地,经过两次下调(或降低)后
的量是a(1
-
x)2.
还要注意根据具体问题的实际意义检验结果的
合理性.
3、(1)小海的爸爸计划在两年后实现家庭年
收入翻一番,那么这两年中收入的平均
年增长率应为多少?
(2)如果调整计划,两年后的收入为原收入
的1.5倍、1.2倍、......那么两年中的平均
年增长率分别为多少?
(3)如果第二年的增长率为第一年的2倍,
那么第一年的增长率为多少时,可以实现
两年后收入翻一番?
例题解析
3、(1)小海的爸爸计划在两年后实现家庭年
收入翻一番,那么这两年中收入的平均
年增长率应为多少?
解:设年收入原为a元,这两年平均年增长率为x.
根据题意,得a(1+x)2=2a
解方程,得x1=-1+
≈41.4%,
x2=-1-
(不合题意,舍去)
答:这两年平均年增长率约为41.4%.
(2)如果调整计划,两年后的收入为原收入的1.5倍、1.2倍,那么两年中的平均年增长率分别为多少?
解:设平均年增长率为x.
根据题意,得(1+x)2=1.5
解方程,得x1=-1+
≈22.5%,
x2=-1-
(不合题意,舍去)
再设平均年增长率为y.
根据题意,得即(1+y)2=1.2
解方程,得x1=-1+
≈9.5%,
x2=-1-
(不合题意,舍去)
答:....,年增长率约为22.5%、9.5%.
(3)如果第二年的增长率为第一年的2倍,
那么第一年的增长率为多少时,可以实现
两年后收入翻一番?
解:设第一年增长率为x,则第二年增长率为2x.
根据题意,得(1+x)(1+2x)=2
解方程,得x1=
≈28.1%,
x2=
(不合题意,舍去)
故第一年的增长率约为28.1%时,可以实现
两年后年收入翻一番。
某种手表,原来每只售价96元,经过
连续2次降价后,现在每只售价54元,
平均每次降价的百分率是多少?
解:设平均每次降价的百分率是x.
由题意,得96
(1-x)
2
=54
解得x1=0.25,
x2=-1.75(不合题意,舍去)
答:平均每次降价的百分率是25%
.
应用练习
知识小结
本节课要掌握:
列一元二次方程解变化率问题.
解决问题的关键是找准每次变化前的基数;
理解公式a(1±x)n=b中每一个字母表示的量;
能区分“翻番”与“倍增”之间的区别;
由具体问题的实际意义检验结果的合理性.
课后作业
列一元二次方程解应用题:
1、某电冰箱厂每个月的产量都比上个月增长
的百分数相同。已知该厂今年4月份的电冰箱
产量为5万台,6月份比5月份多生产了120000
台,求该厂今年产量的月平均增长率为多少?
2、某汽车销售公司2018年盈利1500万元,到
2020年盈利2160万元,且从2018年到2020年,
每年盈利的年增长率相同.(1)该公司2019年盈
利多少万元?(2)若该公司盈利的年增长率继
续保持不变,预计2021年盈利多少万元?
3、2017年某市出口贸易总值为22.52亿美元,
至2019年出口贸易总值达到50.67亿美元.
(1)求这两年该市出口贸易的年平均增长率;
(提示:2252=4×563,5067=9×563)
(2)按这样的速度增长,请你预测2021年该市
的出口贸易总值。
4、在国家政策的宏观调控下,某市的商品房
成交均价由今年6月份的14000元/m2下降到8
月份的12600元/m2.
(1)问4、5两月平均每月
降价的百分率是多少?(参考:
)
(2)如果房价继续回落,按此降价的百分率,
到10月份是否跌破10000元/m2?请说明理由.
22.3实践与探索
3、变化率问题
华东师大版九年级上册
学而不疑则怠,疑而不探则空
知识链接
增加一倍,就是增加了100%;?翻一番,也是增加了100%。除了一倍与一番相当外,两倍与两番以上的数字含义就不同了。而且数字越大,差距越大。如增加两倍,就指增加200%;翻两番,就是400%(一番是二,二番是四,三番就是八),所以说翻两番就是增加了300%,翻三番就是增加了700%。“番”是按几何级数计算的(就是2的x次方),“倍”是按算术级数计算的。
翻番数与增长倍数
列一元二次方程解应用题的思路步骤:
实际
问题
建模
数学
问题
分析
已知量、未知量,等量关系
列出
方程
求
方程的解
验证
合理性
不合理
解释
探索求知
增长率问题:
若用a表示增长(降低)前的数据,x表示
增长率(降低率),b表示变化后的新量,
n表示连续变化的次数,则有公式为:
a(1+x)n=b或a(1-x)n=b
小雨学习非常认真,成绩直线上升,
第一次月考数学成绩是a分,第二次月考增长了10%,
第三次月考又增长了10%,小雨第三次数学成绩是多少?
分析:
第三次
第二次
第一次
a
10%·a
a+10%·a=
a(1+10%)·10%
a(1+10%)+
a(1+10%)·10%
=
a(1+10%)2
a(1+10%)
应用示范
1、天道村的水稻2018年平均每公顷产
8000kg,2020年平均每公顷产9680kg,
求该村水稻每公顷产量的年平均增长率。
例题解析
设该村水稻每公顷产量的年平均增长率为x
(2)根据题意,列出相应方程
解题步骤:
(3)解这个方程,得x1=0.1,x2=-2.1.
(1)用含x的代数式表示:
①2019年种的水稻平均每公顷的产量为
②2020年种的水稻平均每公顷的产量为
8000(1+x)kg
8000(1+x)2kg
8000(1+x)2=9680
(4)检验:x1=0.1,x2=-2.1均为原方程的解,
但x2=-1.1不符合题意,舍去.
(5)答:该村水稻每公顷产量的年平均增长率为10%.
2、西部某区县楼盘准备以每平方米6000元的
均价对外销售,由于新冠疫情的影响,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)大强准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米100元,试问哪种方案更优惠?
例题解析
分析:
设平均每次下调的百分率为x,那么下调一次后
的价格为(6000-6000x)元,即6000(1-x)元,
下调两次后的价格为[6000(1-x)-6000(1-x)·x]元,即6000(1-x)2元,
由题意得,经两次下调后的价格为4860元,
由此可列方程为6000(1-x)2=4860.
解:(1)设平均每次下调的百分率为x,
根据题意,得6000(1-x)2=4860,
解方程,得x1=0.1,x2=1.9(舍去),
故每次下调的百分率为10%.
(2)方案①可以优惠4860×100×(1-0.98)
=9720元;方案②可以优惠100×100
=10000元.所以方案②更优惠。
方法归纳
对于经过两次变化的增长率问题,如果设基数
为a,增长率为x,那么第一次增长后的量为
a+ax,即a(1+x);而a(1+x)又是第二次增长的
基数,增长两次后的量是a(1+x)+a(1+x)x,
即a(1+x)2;同样地,经过两次下调(或降低)后
的量是a(1
-
x)2.
还要注意根据具体问题的实际意义检验结果的
合理性.
3、(1)小海的爸爸计划在两年后实现家庭年
收入翻一番,那么这两年中收入的平均
年增长率应为多少?
(2)如果调整计划,两年后的收入为原收入
的1.5倍、1.2倍、......那么两年中的平均
年增长率分别为多少?
(3)如果第二年的增长率为第一年的2倍,
那么第一年的增长率为多少时,可以实现
两年后收入翻一番?
例题解析
3、(1)小海的爸爸计划在两年后实现家庭年
收入翻一番,那么这两年中收入的平均
年增长率应为多少?
解:设年收入原为a元,这两年平均年增长率为x.
根据题意,得a(1+x)2=2a
解方程,得x1=-1+
≈41.4%,
x2=-1-
(不合题意,舍去)
答:这两年平均年增长率约为41.4%.
(2)如果调整计划,两年后的收入为原收入的1.5倍、1.2倍,那么两年中的平均年增长率分别为多少?
解:设平均年增长率为x.
根据题意,得(1+x)2=1.5
解方程,得x1=-1+
≈22.5%,
x2=-1-
(不合题意,舍去)
再设平均年增长率为y.
根据题意,得即(1+y)2=1.2
解方程,得x1=-1+
≈9.5%,
x2=-1-
(不合题意,舍去)
答:....,年增长率约为22.5%、9.5%.
(3)如果第二年的增长率为第一年的2倍,
那么第一年的增长率为多少时,可以实现
两年后收入翻一番?
解:设第一年增长率为x,则第二年增长率为2x.
根据题意,得(1+x)(1+2x)=2
解方程,得x1=
≈28.1%,
x2=
(不合题意,舍去)
故第一年的增长率约为28.1%时,可以实现
两年后年收入翻一番。
某种手表,原来每只售价96元,经过
连续2次降价后,现在每只售价54元,
平均每次降价的百分率是多少?
解:设平均每次降价的百分率是x.
由题意,得96
(1-x)
2
=54
解得x1=0.25,
x2=-1.75(不合题意,舍去)
答:平均每次降价的百分率是25%
.
应用练习
知识小结
本节课要掌握:
列一元二次方程解变化率问题.
解决问题的关键是找准每次变化前的基数;
理解公式a(1±x)n=b中每一个字母表示的量;
能区分“翻番”与“倍增”之间的区别;
由具体问题的实际意义检验结果的合理性.
课后作业
列一元二次方程解应用题:
1、某电冰箱厂每个月的产量都比上个月增长
的百分数相同。已知该厂今年4月份的电冰箱
产量为5万台,6月份比5月份多生产了120000
台,求该厂今年产量的月平均增长率为多少?
2、某汽车销售公司2018年盈利1500万元,到
2020年盈利2160万元,且从2018年到2020年,
每年盈利的年增长率相同.(1)该公司2019年盈
利多少万元?(2)若该公司盈利的年增长率继
续保持不变,预计2021年盈利多少万元?
3、2017年某市出口贸易总值为22.52亿美元,
至2019年出口贸易总值达到50.67亿美元.
(1)求这两年该市出口贸易的年平均增长率;
(提示:2252=4×563,5067=9×563)
(2)按这样的速度增长,请你预测2021年该市
的出口贸易总值。
4、在国家政策的宏观调控下,某市的商品房
成交均价由今年6月份的14000元/m2下降到8
月份的12600元/m2.
(1)问4、5两月平均每月
降价的百分率是多少?(参考:
)
(2)如果房价继续回落,按此降价的百分率,
到10月份是否跌破10000元/m2?请说明理由.
