新人教版七年级数学上册总复习教案(目标教学)
文档属性
| 名称 | 新人教版七年级数学上册总复习教案(目标教学) |  | |
| 格式 | rar | ||
| 文件大小 | 56.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-09 12:16:12 | ||
图片预览




文档简介
登陆21世纪教育 助您教考全无忧
新人教版(2003年初审通过)七年级数学上册(目标教学模式)
第一章 有理数
[知识回顾]
一、基本概念
1、正数与负数
①表示大小 ②在实际中表示意义相反的量 ③带“-”号的数并不都是负数
2、数轴
原点
①三要素 正方向 ②如何画数轴 ③数轴上的点与有理数
单位长度
3、相反数
①只有符号不同的两个数,叫做互为相反数,0的相反数是0
②a的相反数-a ③a与b互为相反数a+b=0
4、绝对值
①一般地,数轴上表示数a的点与原点距离,表示成|a|。
a (a≥0)
②|a|=
a (a≤0)
5、倒数
①乘积是1的两个数叫作互为倒数。 ②a的倒数是(a≠0)
③a与b互为倒数ab=1
6、相反数是它本身的数是0
①倒数是它本身的数是±1 ②绝对值是它本身的数是非负数
③平方等于它本身的数是0,1 ④立方等于经本身的数是±1,0
7、乘方
①求几个相同因数的积的运算叫做乘方a·a·…·a=an
②底数、指数、幂
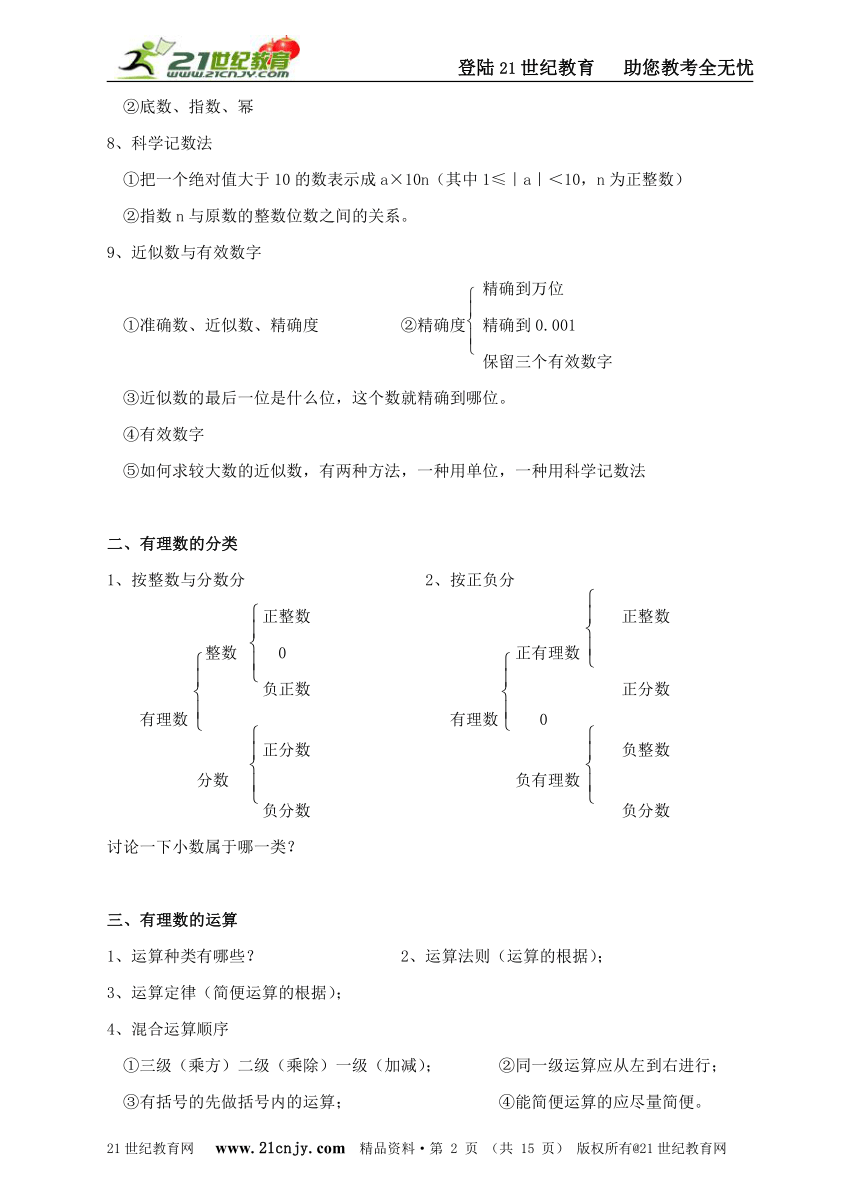
8、科学记数法
①把一个绝对值大于10的数表示成a×10n(其中1≤|a|<10,n为正整数)
②指数n与原数的整数位数之间的关系。
9、近似数与有效数字
精确到万位
①准确数、近似数、精确度 ②精确度 精确到0.001
保留三个有效数字
③近似数的最后一位是什么位,这个数就精确到哪位。
④有效数字
⑤如何求较大数的近似数,有两种方法,一种用单位,一种用科学记数法
二、有理数的分类
1、按整数与分数分 2、按正负分
正整数 正整数
整数 0 正有理数
负正数 正分数
有理数 有理数 0
正分数 负整数
分数 负有理数
负分数 负分数
讨论一下小数属于哪一类?
三、有理数的运算
1、运算种类有哪些? 2、运算法则(运算的根据);
3、运算定律(简便运算的根据);
4、混合运算顺序
①三级(乘方)二级(乘除)一级(加减); ②同一级运算应从左到右进行;
③有括号的先做括号内的运算; ④能简便运算的应尽量简便。
四、课堂练习与作业
1、下列语句正确的的( )个
(1)带“-”号的数是负数 (2)如果a为正数,则- a一定是负数
(3)不存在既不是正数又不是负数的数 (4)00C表示没有温度
A、0 B、1 C、2 D、3
2、最小的整数是( )
A、- 1 B、0 C、1 D、不存在
3、向东走10米记作+10米,则向西走8米记作___________
4、在- ,π,0,0.333……,3.14,- 10中,有理数有( )个
A、1 B、2 C、4 D、5
5、正整数集合与负整数集合合并在一起构成( )
A、整数集合 B、有理数集合 C、自然数集合 D、以上都不对
6、有理数中,最小的正整数是_________,最大的负整数是___________
7、下列说法错误的是( )
A、数轴是一条直线; B、表示- 1的点,离原点1个单位长度;
C、数轴上表示- 3的点与表示- 1的点相距2个单位长度;
D、距原点3个单位长度的点表示—3或3。
8、数轴上表示整数的点称为整点某数轴的单位长度为1cm,若在数轴上随意画出一条长2005cm长的线段AB,则线段AB盖住的的整点有( )个
A、2003或2004 B、2004或2005; C、2005或2006; D、2006或2007
9、- 3的相反数、绝对值、倒数分别是___________________________;
10、- a表示的数是( )
A、负数 B、正数 C、正数或负数 D、a的相反数
11、若|x+1|=2,则x=_______________;
12、若|x+2|+(y-3)2=0,则=______________;
13、若|a|+|b|=4,且a=- 3,则b=_________;
14、下列叙述正确的是( )
A、若|a|=|b|,则a=b B、若|a|>|b|,则a>b
C、若a15、当a<0时,7a+8|a|= ______________;
16、下列名组数中,相等的一组是( )
A、(- 3)3与—33 B、(- 3)2与- 32
C、43与34 D、- 32与(- 3)+(- 3)
17、(- 2)2004+(- 2)2005=__________________
18、我国某石油产量为170000000吨,用科学记数法表示为__________________;
19、近似数0.0302精确到______ 位,有__________个有效数字。
20、(-1)+(-1)2+(-1)3+……+(-1)2005=__________________;
A、-2005 B、2005 C、-1 D、1
21、若两数之和为负数,则这两个数一定是( )
A、同为正数 B、同为负数 C、一正一负 D、无法确定
22、已知有理数a,b,c在数轴上的位置如图所示,
下列错误的是( )
A、b+c<0 B、-a+b+c<0 c b 0 a
C、|a+b|<|a+c| D、|a+b|>|a+c|
23、若b<0,则a,a+b,a-b中最大的是( )
A、a B、a+b C、a-b D、还要看a的符号才能确定
24、计算( )×(-12)=________________
25、绝对值小于5的所有整数有__________________________;
26、用“<”符号连接:-3,1,0,(-3)2,-12为__________________________;
27、已知a与b互为相反数,c与d互为倒数,m的绝对值为2,求 -cd+m的值。
28、已知有理数a,b,c在数轴上对应点如图秘示,
化简|a-b|+|b-c|-|c-a|。 c 0 b a
第二章 整式的加减
[知识回顾]
1、______和______统称整式。
①单项式:由 与 的乘积式子称为单项式。单独一个数或一个字母也是单项式,如a ,5。
·单项式的系数:单式项里的 叫做单项式的系数。
·单项式的次数:单项式中 叫做单项式的次数。
②多项式:几个 的和叫做多项式。其中,每个单项式叫做多项式的 ,不含字母的项叫做 。
·多项式的次数:多项式里 的次数,叫做多项式的次数。
·多项式的命:一个多项式含有几项,就叫几项式。所以我们就根据多项式的项数和次数来命名一个多项式。如:3n4-2n2+1是一个四次三项式。
2、同类项——必须同时具备的两个条件(缺一不可):
①所含的 相同;
②相同 也相同。
·合并同类项,就是把多项式中的同类项合并成一项。
方法:把各项的 相加,而 不变。
3、去括号法则
法则1.括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都 符号;
法则2.括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都 符号。
▲去括号法则的依据实际是 。
〖注意1〗要注意括号前面的符号,它是去括号后括号内各项是否变号的依据.
〖注意2〗去括号时应将括号前的符号连同括号一起去掉.
〖注意3〗括号前面是“-”时,去掉括号后,括号内的各项均要改变符号,不能只改变括号内第一项或前几项的符号,而忘记改变其余的符号. 若括号前是数字因数时,可运用乘法分配律先将数与括号内的各项分别相乘再去括号,以免发生错误.
〖注意4〗遇到多层括号一般由里到外,逐层去括号,也可由外到里.数“-”的个数.
4、整式的加减
整式的加减的过程就是 。如遇到括号,则先 ,再 ,合并到 为止。
5、本单元需要注意的几个问题
①整式(既单项式和多项式)中,分母一律不能含有字母。
②π不是字母,而是一个数字,
③多项式相加(减)时,必须用括号把多项式括起来,才能进行计算。
④去括号时,要特别注意括号前面的因数。
二、课堂练习与作业
1、在,中,
单项式有:
多项式有: 。
2、填一填
整式 -ab πr2 -a+b A3b2-2a2b2+b3-7ab+5
系数
次数
项
3、一种商品每件a元,按成本增加20%定出的价格是 ;后来因库存积压,又以原价的八五折出售,则现价是 元;每件还能盈利 元。
4、已知-7x2ym是7次单项式则m= 。
5、已知-5xmy3与4x3yn能合并,则mn = 。
6、7-2xy-3x2y3+5x3y2z-9x4y3z2是 次 项式,其中最高次项是 ,最高次项的系数是 ,常数项是 ,是按字母 作 幂排列。
7、-3a+3a=-3( ), 2 a-2a=2( ),
-5 a-5a=-5( ), 4a + 4a= 4 ( ),
8、已知x-y=5,xy=3,则3xy-7x+7y= 。
9、已知A=3x+1,B=6x-3,则3A-B= 。
10、计算
①(a3-2a2+1)-2(3a2-2a+) ②x-2(1-2x+x2)+3(-2+3x-x2)
11、已知ab=3,a+b=4,求3ab-[2a - (2ab-2b)+3]的值。
12、若(x2+ax-2y+7)―(bx2―2x+9 y-1)的值与字母x的取值无关,求a、b的值。
第三章 一元一次方程
[知识回顾]
一、主要概念
1、方程:含有未知数的等式叫做方程。
2、一元一次方程:只含有一个未知数,未知数的指数是1的方程叫做一元一次方程。
3、方程的解:使方程左右两边相等的未知数的值叫做方程的解。
4、解方程:求方程的解的过程叫做解方程。
二、等式的性质
等式的性质1:等式两边都加(或减)同一个数(或式子),结果仍相等。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
三、解一元一次方程的一般步骤及根据
1、去分母-------------------等式的性质2
2、去括号-------------------分配律
3、移项----------------------等式的性质1
4、合并----------------------分配律
5、系数化为1--------------等式的性质2
6、验根--------------------把根分别代入方程的左右边看求得的值是否相等
四、解一元一次方程的注意事项
1、分母是小数时,根据分数的基本性质,把分母转化为整数;
2、去分母时,方程两边各项都乘各分母的最小公倍数,此时不含分母的项切勿
漏乘,分数线相当于括号,去分母后分子各项应加括号;
3、去括号时,不要漏乘括号内的项,不要弄错符号;
4、移项时,切记要变号,不要丢项,有时先合并再移项,以免丢项;
5、系数化为1时,方程两边同乘以系数的倒数或同除以系数,不要弄错符号;
6、不要生搬硬套解方程的步骤,具体问题具体分析,找到最佳解法。
五、列方程解应用题的一般步骤
1、审题 2、设未数 3、找相等关系 4、列方程
5、解方程 6、检验 7、写出答案
六、课堂练习与作业
1、下列是一元一次方程的是( )
A、2x+1 B、x+2y=1 C、x2+2=0 D、x=3
2、解为x=-3的方程是( )
A、2x-6=0 B、=6 C、3(x-2)-2(x-3)=5x D、
3、下列说法错误的是( )
A、若 = ,则x=y B、若x2=y2,则-4ax2=-4ay2
C、若- x=-6,则x= D、若1=x,则x=1
4、已知2x2-3=7,则x2+1=_______
5、已知ax=ay,下列等式不一定成立的是( )
A、b+ax=b+ay B、x=y C、ax-y=ay-y D、
6、下列方程由前一方程变到后一方程,正确的是( )
A、9x=4,x=- B、5x=- ,x=-
C、0.2x=1,x=0.2 D、-0.5x=- ,x=1
7、方程2x-kx+1=5x-2的解是-1时,k=_______
8、解方程2(x-2)-3(4x-1)=9,下列解答正确的是( )
A、2x-4-12x+3=9,-10x=9+4-3=10,x=1; B、2x-4-12x+3=9,-10x=10,x=-1
C、2x-4-12x-3=9,-10x=2,x=- ; D、2x-4-12x-3=9,-10x=10,x=1
9、如果=6与 的值相等,则x=_________
10、已知方程 3x+8=-a的解满足|x-2|=0,则 =_______
11、若方程3x+5=11与6x+3a=22的解相同,则a=______
12、某书中一道方程题 +1=x, 处在印刷时被墨盖住了,查后面的答案,这道方程的解为x=-2.5,则 处的数 字为( )
A、-2.5 B、2.5 C、5 D、7
13、已知3x+1=7,则2x+2=_______
14、|3x-2|=4,则x=____________
15、已知2xm-1+4=0是一元一次方程,则m=________
16、解方程
(1)1+17x=8x+3 (2)2(x+3)-5(1-x)=3(x-1)
(3)-(x-5)= - (4)+8x=+4
17、已知关于x的方程(m+1)x|m|+3=0是一元一次方程,求m2-2+3m的值。
18、若(2x-1)3=a+bx+cx2+dx3, 要求a+b+c+d的值,可令x=1,原等式变形为
(2×1-1)3=a+b+c+d,所以a+b+c+d=1,想一想,利用上述a+b+c+d的方法,
能不能求
(1)a的值
(2)a+c的值?若能,写出解答过程。若不能,请说明理由。
22、商场出售两种冰箱:A型冰箱每台售价2190元,每日耗电量为1度;B型冰箱每台售价比A型冰箱高出10﹪,每日耗电量为0.55度。现将A型冰箱打八五折出售。按使用期都是10年,每年都为365天,每度电费0.4元计算。问购买A型冰箱合算吗?若不合算,A型冰箱至少要折几折才合算?
第四章 图形初步认识
[知识回顾]
(一)多姿多彩的图形
立体图形:棱柱、棱锥、圆柱、圆锥、球等。
1、几何图形
平面图形:三角形、四边形、圆等。
主(正)视图---------从正面看
2、几何体的三视图 侧(左、右)视图-----从左(右)边看
俯视图---------------从上面看
(1)会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图。
(2)能根据三视图描述基本几何体或实物原型。
3、立体图形的平面展开图
(1)同一个立体图形按不同的方式展开,得到的平现图形不一样的。
(2)了解直棱柱、圆柱、圆锥、的平面展开图,能根据展开图判断和制作立体模型。
4、点、线、面、体
(1)几何图形的组成
点:线和线相交的地方是点,它是几何图形最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
(2)点动成线,线动成面,面动成体。
(二)直线、射线、线段
1、基本概念
直线 射线 线段
图形
端点个数 无 一个 两个
表示法 直线a,直线AB(BA) 射线AB 线段a,线段AB(BA)
作法叙述 作直线AB;作直线a 作射线AB 作线段a;作线段AB;连接AB
延长叙述 不能延长 反向延长射线AB 延长线段AB;反向延长线段BA
2、直线的性质
经过两点有一条直线,并且只有一条直线。简单地:两点确定一条直线。
3、画一条线段等于已知线段
(1)度量法 (2)用尺规作图法
4、线段的大小比较方法
(1)度量法 (2)叠合法
5、线段的中点(二等分点)、三等分点、四等分点等
定义:把一条线段平均分成两条相等线段的点。
图形:
A M B
符号:若点M是线段AB的中点,则AM=BM=AB,AB=2AM=2BM。
6、线段的性质
两点的所有连线中,线段最短。简单地:两点之间,线段最短。
7、两点的距离
连接两点的线段长度叫做两点的距离。
8、点与直线的位置关系
(1)点在直线上 (2)点在直线外。
(三)角
1、角:由公共端点的两条射线所组成的图形叫做角。 2、角的表示法(四种):
3、角的度量单位及换算 4、角的分类
∠β 锐角 直角 钝角 平角 周角
范围 0<∠β<90° ∠β=90° 90°<∠β<180° ∠β=180° ∠β=360°
5、角的比较方法
(1)度量法 (2)叠合法
6、角的和、差、倍、分及其近似值
7、画一个角等于已知角
(1)借助三角尺能画出15°的倍数的角,在0~180°之间共能画出11个角。
(2)借助量角器能画出给定度数的角。
(3)用尺规作图法。
8、角的平线线
定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线。
9、互余、互补
(1)若∠1+∠2=90°,则∠1与∠2互为余角。其中∠1是∠2的余角,∠2是∠1的余角。
(2)若∠1+∠2=180°,则∠1与∠2互为补角。其中∠1是∠2的补角,∠2是∠1的补角。
(3)余(补)角的性质:等角的补(余)角相等。
10、方向角
(1)正方向
(2)北(南)偏东(西)方向
(3)东(西)北(南)方向
四、课堂练习与作业
1、下列说法中正确的是( )
A、延长射线OP B、延长直线CD C、延长线段CD D、反向延长直线CD
2、下面是我们制作的正方体的展开图,每个平面内都标注了字母,请根据要求回答问题:
(1)和面A所对的会是哪一面?
(2)和B面所对的会是哪一面?
(3)面E会和哪些面相交?
3、 两条直线相交有几个交点?
三条直线两两相交有几个交点?
四条直线两两相交有几个交点?
思考:n条直线两两相交有几个交点?
4、 已知平面内有四个点A、B、C、D,过其中任意两点画直线,最少可画多少条直线,
最多可画多少条直线?画出图来.
5、已知点C是线段AB的中点,点D是线段BC的中点,CD=2.5厘米,请你求出线段AB、AC、AD、BD的长各为多少?
6、已知线段AB=4厘米,延长AB到C,使B C=2AB,取AC的中点P,求PB的长.
7、计算:30.26°=____ °____′____″; 18°15′36″ =____ __ °;
36°56′+18°14′=____ ; 108°- 56°23′ =________;
27°17′×5 =____ ; 15°20′÷6 =____ (精确到分)
8、 60°=____平角 ;直角=______度;周角=______度。
9、 如图,∠ACB = 90°,∠CDA = 90°,写出图中
(1)所有的线段:_______________;
(2)所有的锐角:________________
(3)与∠CDA互补的角:_______________
10、如图:AOC= + __
BOC=BOD- =AOC-
11、如图, BC=4cm,BD=7cm,且D是AC的中点,则AC=________
12.已知点A、B、C三个点在同一条直线上,若线段AB=8,BC=5,则线段AC=_________
13、一个角与它的余角相等,则这个角是______,它的补角是_______
14、三点半时,时针和分针之间所形的成的(小于平角)角的度数是_______
15、若∠1∶∠2∶∠3∶∠4=1∶2∶3∶4,四个角的和为180°,则∠2=______;∠3=______;1与4互为 角。
《去(添)括号法则[记法]》
去括号、添括号,
符号变化最重要。
括号前面是正号,
里面各项保留好*。
括号前面是负号,
里面各项都变号
[*“各项保留好”指保留项的符号不变]
13、求5ab-2[3ab- (4ab2+ab)] -5ab2的值,其中a=,b=-
14、如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有n(n>1)个点,每个图形总的点数S是多少?当n=7,100时,S是多少?
(第10题)
B
D
C
A
(第9题)
.
.
.
.
A
D
C
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 15 页) 版权所有@21世纪教育网
新人教版(2003年初审通过)七年级数学上册(目标教学模式)
第一章 有理数
[知识回顾]
一、基本概念
1、正数与负数
①表示大小 ②在实际中表示意义相反的量 ③带“-”号的数并不都是负数
2、数轴
原点
①三要素 正方向 ②如何画数轴 ③数轴上的点与有理数
单位长度
3、相反数
①只有符号不同的两个数,叫做互为相反数,0的相反数是0
②a的相反数-a ③a与b互为相反数a+b=0
4、绝对值
①一般地,数轴上表示数a的点与原点距离,表示成|a|。
a (a≥0)
②|a|=
a (a≤0)
5、倒数
①乘积是1的两个数叫作互为倒数。 ②a的倒数是(a≠0)
③a与b互为倒数ab=1
6、相反数是它本身的数是0
①倒数是它本身的数是±1 ②绝对值是它本身的数是非负数
③平方等于它本身的数是0,1 ④立方等于经本身的数是±1,0
7、乘方
①求几个相同因数的积的运算叫做乘方a·a·…·a=an
②底数、指数、幂
8、科学记数法
①把一个绝对值大于10的数表示成a×10n(其中1≤|a|<10,n为正整数)
②指数n与原数的整数位数之间的关系。
9、近似数与有效数字
精确到万位
①准确数、近似数、精确度 ②精确度 精确到0.001
保留三个有效数字
③近似数的最后一位是什么位,这个数就精确到哪位。
④有效数字
⑤如何求较大数的近似数,有两种方法,一种用单位,一种用科学记数法
二、有理数的分类
1、按整数与分数分 2、按正负分
正整数 正整数
整数 0 正有理数
负正数 正分数
有理数 有理数 0
正分数 负整数
分数 负有理数
负分数 负分数
讨论一下小数属于哪一类?
三、有理数的运算
1、运算种类有哪些? 2、运算法则(运算的根据);
3、运算定律(简便运算的根据);
4、混合运算顺序
①三级(乘方)二级(乘除)一级(加减); ②同一级运算应从左到右进行;
③有括号的先做括号内的运算; ④能简便运算的应尽量简便。
四、课堂练习与作业
1、下列语句正确的的( )个
(1)带“-”号的数是负数 (2)如果a为正数,则- a一定是负数
(3)不存在既不是正数又不是负数的数 (4)00C表示没有温度
A、0 B、1 C、2 D、3
2、最小的整数是( )
A、- 1 B、0 C、1 D、不存在
3、向东走10米记作+10米,则向西走8米记作___________
4、在- ,π,0,0.333……,3.14,- 10中,有理数有( )个
A、1 B、2 C、4 D、5
5、正整数集合与负整数集合合并在一起构成( )
A、整数集合 B、有理数集合 C、自然数集合 D、以上都不对
6、有理数中,最小的正整数是_________,最大的负整数是___________
7、下列说法错误的是( )
A、数轴是一条直线; B、表示- 1的点,离原点1个单位长度;
C、数轴上表示- 3的点与表示- 1的点相距2个单位长度;
D、距原点3个单位长度的点表示—3或3。
8、数轴上表示整数的点称为整点某数轴的单位长度为1cm,若在数轴上随意画出一条长2005cm长的线段AB,则线段AB盖住的的整点有( )个
A、2003或2004 B、2004或2005; C、2005或2006; D、2006或2007
9、- 3的相反数、绝对值、倒数分别是___________________________;
10、- a表示的数是( )
A、负数 B、正数 C、正数或负数 D、a的相反数
11、若|x+1|=2,则x=_______________;
12、若|x+2|+(y-3)2=0,则=______________;
13、若|a|+|b|=4,且a=- 3,则b=_________;
14、下列叙述正确的是( )
A、若|a|=|b|,则a=b B、若|a|>|b|,则a>b
C、若a
16、下列名组数中,相等的一组是( )
A、(- 3)3与—33 B、(- 3)2与- 32
C、43与34 D、- 32与(- 3)+(- 3)
17、(- 2)2004+(- 2)2005=__________________
18、我国某石油产量为170000000吨,用科学记数法表示为__________________;
19、近似数0.0302精确到______ 位,有__________个有效数字。
20、(-1)+(-1)2+(-1)3+……+(-1)2005=__________________;
A、-2005 B、2005 C、-1 D、1
21、若两数之和为负数,则这两个数一定是( )
A、同为正数 B、同为负数 C、一正一负 D、无法确定
22、已知有理数a,b,c在数轴上的位置如图所示,
下列错误的是( )
A、b+c<0 B、-a+b+c<0 c b 0 a
C、|a+b|<|a+c| D、|a+b|>|a+c|
23、若b<0,则a,a+b,a-b中最大的是( )
A、a B、a+b C、a-b D、还要看a的符号才能确定
24、计算( )×(-12)=________________
25、绝对值小于5的所有整数有__________________________;
26、用“<”符号连接:-3,1,0,(-3)2,-12为__________________________;
27、已知a与b互为相反数,c与d互为倒数,m的绝对值为2,求 -cd+m的值。
28、已知有理数a,b,c在数轴上对应点如图秘示,
化简|a-b|+|b-c|-|c-a|。 c 0 b a
第二章 整式的加减
[知识回顾]
1、______和______统称整式。
①单项式:由 与 的乘积式子称为单项式。单独一个数或一个字母也是单项式,如a ,5。
·单项式的系数:单式项里的 叫做单项式的系数。
·单项式的次数:单项式中 叫做单项式的次数。
②多项式:几个 的和叫做多项式。其中,每个单项式叫做多项式的 ,不含字母的项叫做 。
·多项式的次数:多项式里 的次数,叫做多项式的次数。
·多项式的命:一个多项式含有几项,就叫几项式。所以我们就根据多项式的项数和次数来命名一个多项式。如:3n4-2n2+1是一个四次三项式。
2、同类项——必须同时具备的两个条件(缺一不可):
①所含的 相同;
②相同 也相同。
·合并同类项,就是把多项式中的同类项合并成一项。
方法:把各项的 相加,而 不变。
3、去括号法则
法则1.括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都 符号;
法则2.括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都 符号。
▲去括号法则的依据实际是 。
〖注意1〗要注意括号前面的符号,它是去括号后括号内各项是否变号的依据.
〖注意2〗去括号时应将括号前的符号连同括号一起去掉.
〖注意3〗括号前面是“-”时,去掉括号后,括号内的各项均要改变符号,不能只改变括号内第一项或前几项的符号,而忘记改变其余的符号. 若括号前是数字因数时,可运用乘法分配律先将数与括号内的各项分别相乘再去括号,以免发生错误.
〖注意4〗遇到多层括号一般由里到外,逐层去括号,也可由外到里.数“-”的个数.
4、整式的加减
整式的加减的过程就是 。如遇到括号,则先 ,再 ,合并到 为止。
5、本单元需要注意的几个问题
①整式(既单项式和多项式)中,分母一律不能含有字母。
②π不是字母,而是一个数字,
③多项式相加(减)时,必须用括号把多项式括起来,才能进行计算。
④去括号时,要特别注意括号前面的因数。
二、课堂练习与作业
1、在,中,
单项式有:
多项式有: 。
2、填一填
整式 -ab πr2 -a+b A3b2-2a2b2+b3-7ab+5
系数
次数
项
3、一种商品每件a元,按成本增加20%定出的价格是 ;后来因库存积压,又以原价的八五折出售,则现价是 元;每件还能盈利 元。
4、已知-7x2ym是7次单项式则m= 。
5、已知-5xmy3与4x3yn能合并,则mn = 。
6、7-2xy-3x2y3+5x3y2z-9x4y3z2是 次 项式,其中最高次项是 ,最高次项的系数是 ,常数项是 ,是按字母 作 幂排列。
7、-3a+3a=-3( ), 2 a-2a=2( ),
-5 a-5a=-5( ), 4a + 4a= 4 ( ),
8、已知x-y=5,xy=3,则3xy-7x+7y= 。
9、已知A=3x+1,B=6x-3,则3A-B= 。
10、计算
①(a3-2a2+1)-2(3a2-2a+) ②x-2(1-2x+x2)+3(-2+3x-x2)
11、已知ab=3,a+b=4,求3ab-[2a - (2ab-2b)+3]的值。
12、若(x2+ax-2y+7)―(bx2―2x+9 y-1)的值与字母x的取值无关,求a、b的值。
第三章 一元一次方程
[知识回顾]
一、主要概念
1、方程:含有未知数的等式叫做方程。
2、一元一次方程:只含有一个未知数,未知数的指数是1的方程叫做一元一次方程。
3、方程的解:使方程左右两边相等的未知数的值叫做方程的解。
4、解方程:求方程的解的过程叫做解方程。
二、等式的性质
等式的性质1:等式两边都加(或减)同一个数(或式子),结果仍相等。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
三、解一元一次方程的一般步骤及根据
1、去分母-------------------等式的性质2
2、去括号-------------------分配律
3、移项----------------------等式的性质1
4、合并----------------------分配律
5、系数化为1--------------等式的性质2
6、验根--------------------把根分别代入方程的左右边看求得的值是否相等
四、解一元一次方程的注意事项
1、分母是小数时,根据分数的基本性质,把分母转化为整数;
2、去分母时,方程两边各项都乘各分母的最小公倍数,此时不含分母的项切勿
漏乘,分数线相当于括号,去分母后分子各项应加括号;
3、去括号时,不要漏乘括号内的项,不要弄错符号;
4、移项时,切记要变号,不要丢项,有时先合并再移项,以免丢项;
5、系数化为1时,方程两边同乘以系数的倒数或同除以系数,不要弄错符号;
6、不要生搬硬套解方程的步骤,具体问题具体分析,找到最佳解法。
五、列方程解应用题的一般步骤
1、审题 2、设未数 3、找相等关系 4、列方程
5、解方程 6、检验 7、写出答案
六、课堂练习与作业
1、下列是一元一次方程的是( )
A、2x+1 B、x+2y=1 C、x2+2=0 D、x=3
2、解为x=-3的方程是( )
A、2x-6=0 B、=6 C、3(x-2)-2(x-3)=5x D、
3、下列说法错误的是( )
A、若 = ,则x=y B、若x2=y2,则-4ax2=-4ay2
C、若- x=-6,则x= D、若1=x,则x=1
4、已知2x2-3=7,则x2+1=_______
5、已知ax=ay,下列等式不一定成立的是( )
A、b+ax=b+ay B、x=y C、ax-y=ay-y D、
6、下列方程由前一方程变到后一方程,正确的是( )
A、9x=4,x=- B、5x=- ,x=-
C、0.2x=1,x=0.2 D、-0.5x=- ,x=1
7、方程2x-kx+1=5x-2的解是-1时,k=_______
8、解方程2(x-2)-3(4x-1)=9,下列解答正确的是( )
A、2x-4-12x+3=9,-10x=9+4-3=10,x=1; B、2x-4-12x+3=9,-10x=10,x=-1
C、2x-4-12x-3=9,-10x=2,x=- ; D、2x-4-12x-3=9,-10x=10,x=1
9、如果=6与 的值相等,则x=_________
10、已知方程 3x+8=-a的解满足|x-2|=0,则 =_______
11、若方程3x+5=11与6x+3a=22的解相同,则a=______
12、某书中一道方程题 +1=x, 处在印刷时被墨盖住了,查后面的答案,这道方程的解为x=-2.5,则 处的数 字为( )
A、-2.5 B、2.5 C、5 D、7
13、已知3x+1=7,则2x+2=_______
14、|3x-2|=4,则x=____________
15、已知2xm-1+4=0是一元一次方程,则m=________
16、解方程
(1)1+17x=8x+3 (2)2(x+3)-5(1-x)=3(x-1)
(3)-(x-5)= - (4)+8x=+4
17、已知关于x的方程(m+1)x|m|+3=0是一元一次方程,求m2-2+3m的值。
18、若(2x-1)3=a+bx+cx2+dx3, 要求a+b+c+d的值,可令x=1,原等式变形为
(2×1-1)3=a+b+c+d,所以a+b+c+d=1,想一想,利用上述a+b+c+d的方法,
能不能求
(1)a的值
(2)a+c的值?若能,写出解答过程。若不能,请说明理由。
22、商场出售两种冰箱:A型冰箱每台售价2190元,每日耗电量为1度;B型冰箱每台售价比A型冰箱高出10﹪,每日耗电量为0.55度。现将A型冰箱打八五折出售。按使用期都是10年,每年都为365天,每度电费0.4元计算。问购买A型冰箱合算吗?若不合算,A型冰箱至少要折几折才合算?
第四章 图形初步认识
[知识回顾]
(一)多姿多彩的图形
立体图形:棱柱、棱锥、圆柱、圆锥、球等。
1、几何图形
平面图形:三角形、四边形、圆等。
主(正)视图---------从正面看
2、几何体的三视图 侧(左、右)视图-----从左(右)边看
俯视图---------------从上面看
(1)会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图。
(2)能根据三视图描述基本几何体或实物原型。
3、立体图形的平面展开图
(1)同一个立体图形按不同的方式展开,得到的平现图形不一样的。
(2)了解直棱柱、圆柱、圆锥、的平面展开图,能根据展开图判断和制作立体模型。
4、点、线、面、体
(1)几何图形的组成
点:线和线相交的地方是点,它是几何图形最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
(2)点动成线,线动成面,面动成体。
(二)直线、射线、线段
1、基本概念
直线 射线 线段
图形
端点个数 无 一个 两个
表示法 直线a,直线AB(BA) 射线AB 线段a,线段AB(BA)
作法叙述 作直线AB;作直线a 作射线AB 作线段a;作线段AB;连接AB
延长叙述 不能延长 反向延长射线AB 延长线段AB;反向延长线段BA
2、直线的性质
经过两点有一条直线,并且只有一条直线。简单地:两点确定一条直线。
3、画一条线段等于已知线段
(1)度量法 (2)用尺规作图法
4、线段的大小比较方法
(1)度量法 (2)叠合法
5、线段的中点(二等分点)、三等分点、四等分点等
定义:把一条线段平均分成两条相等线段的点。
图形:
A M B
符号:若点M是线段AB的中点,则AM=BM=AB,AB=2AM=2BM。
6、线段的性质
两点的所有连线中,线段最短。简单地:两点之间,线段最短。
7、两点的距离
连接两点的线段长度叫做两点的距离。
8、点与直线的位置关系
(1)点在直线上 (2)点在直线外。
(三)角
1、角:由公共端点的两条射线所组成的图形叫做角。 2、角的表示法(四种):
3、角的度量单位及换算 4、角的分类
∠β 锐角 直角 钝角 平角 周角
范围 0<∠β<90° ∠β=90° 90°<∠β<180° ∠β=180° ∠β=360°
5、角的比较方法
(1)度量法 (2)叠合法
6、角的和、差、倍、分及其近似值
7、画一个角等于已知角
(1)借助三角尺能画出15°的倍数的角,在0~180°之间共能画出11个角。
(2)借助量角器能画出给定度数的角。
(3)用尺规作图法。
8、角的平线线
定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线。
9、互余、互补
(1)若∠1+∠2=90°,则∠1与∠2互为余角。其中∠1是∠2的余角,∠2是∠1的余角。
(2)若∠1+∠2=180°,则∠1与∠2互为补角。其中∠1是∠2的补角,∠2是∠1的补角。
(3)余(补)角的性质:等角的补(余)角相等。
10、方向角
(1)正方向
(2)北(南)偏东(西)方向
(3)东(西)北(南)方向
四、课堂练习与作业
1、下列说法中正确的是( )
A、延长射线OP B、延长直线CD C、延长线段CD D、反向延长直线CD
2、下面是我们制作的正方体的展开图,每个平面内都标注了字母,请根据要求回答问题:
(1)和面A所对的会是哪一面?
(2)和B面所对的会是哪一面?
(3)面E会和哪些面相交?
3、 两条直线相交有几个交点?
三条直线两两相交有几个交点?
四条直线两两相交有几个交点?
思考:n条直线两两相交有几个交点?
4、 已知平面内有四个点A、B、C、D,过其中任意两点画直线,最少可画多少条直线,
最多可画多少条直线?画出图来.
5、已知点C是线段AB的中点,点D是线段BC的中点,CD=2.5厘米,请你求出线段AB、AC、AD、BD的长各为多少?
6、已知线段AB=4厘米,延长AB到C,使B C=2AB,取AC的中点P,求PB的长.
7、计算:30.26°=____ °____′____″; 18°15′36″ =____ __ °;
36°56′+18°14′=____ ; 108°- 56°23′ =________;
27°17′×5 =____ ; 15°20′÷6 =____ (精确到分)
8、 60°=____平角 ;直角=______度;周角=______度。
9、 如图,∠ACB = 90°,∠CDA = 90°,写出图中
(1)所有的线段:_______________;
(2)所有的锐角:________________
(3)与∠CDA互补的角:_______________
10、如图:AOC= + __
BOC=BOD- =AOC-
11、如图, BC=4cm,BD=7cm,且D是AC的中点,则AC=________
12.已知点A、B、C三个点在同一条直线上,若线段AB=8,BC=5,则线段AC=_________
13、一个角与它的余角相等,则这个角是______,它的补角是_______
14、三点半时,时针和分针之间所形的成的(小于平角)角的度数是_______
15、若∠1∶∠2∶∠3∶∠4=1∶2∶3∶4,四个角的和为180°,则∠2=______;∠3=______;1与4互为 角。
《去(添)括号法则[记法]》
去括号、添括号,
符号变化最重要。
括号前面是正号,
里面各项保留好*。
括号前面是负号,
里面各项都变号
[*“各项保留好”指保留项的符号不变]
13、求5ab-2[3ab- (4ab2+ab)] -5ab2的值,其中a=,b=-
14、如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有n(n>1)个点,每个图形总的点数S是多少?当n=7,100时,S是多少?
(第10题)
B
D
C
A
(第9题)
.
.
.
.
A
D
C
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 15 页) 版权所有@21世纪教育网
