人教版八年级上册 数学 课件 13.4 课题学习 最短路径问题(25张)
文档属性
| 名称 | 人教版八年级上册 数学 课件 13.4 课题学习 最短路径问题(25张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 403.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 00:00:00 | ||
图片预览





文档简介
13.4 课题学习 最短路径问题
将军饮马问题:
早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:
将军每天骑马从城堡A出发,到城堡B,途中
马要到小河边饮水一次。将军问怎样走路程最短?
这就是广为流传的"将军饮马"问题。
P
两点之间线段最短.
根据:
B
A
(一)两点在一条直线两侧
例1.如图:古希腊一位将军骑马从城堡A到城堡B,途中
马要到小溪边饮水一次。问将军怎样走路程最短?
最短路线:
(
分类讨论:
A ---P--- B.
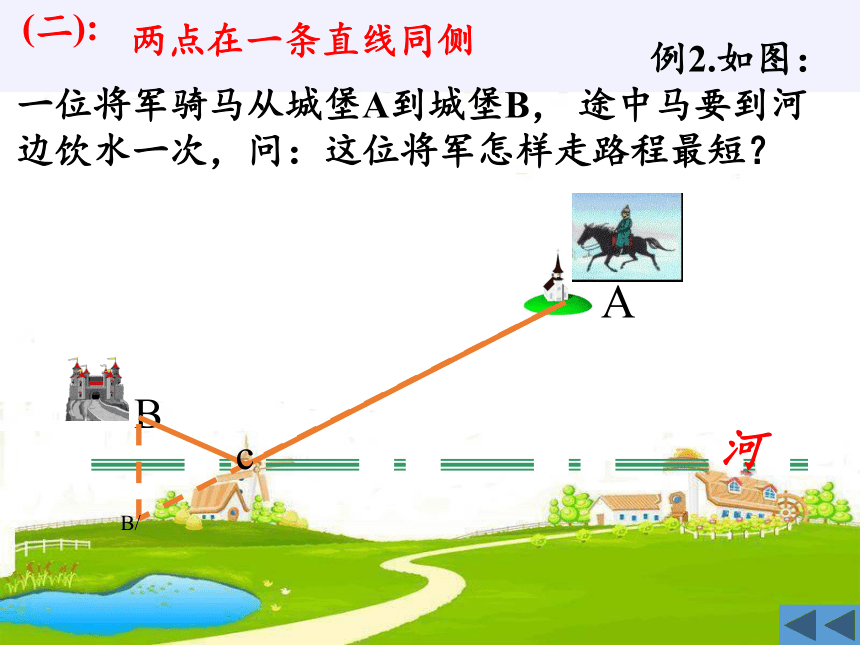
例2.如图:一位将军骑马从城堡A到城堡B, 途中马要到河边饮水一次,问:这位将军怎样走路程最短?
A
B
河
两点在一条直线同侧
(二):
B/
c
例2变式:已知:P、Q是△ABC的边AB、
AC上的点,你能在BC上确定一点R,
使△PQR的周长最短吗?
两点在一条直线同侧
(二)一次轴对称:
p/
R
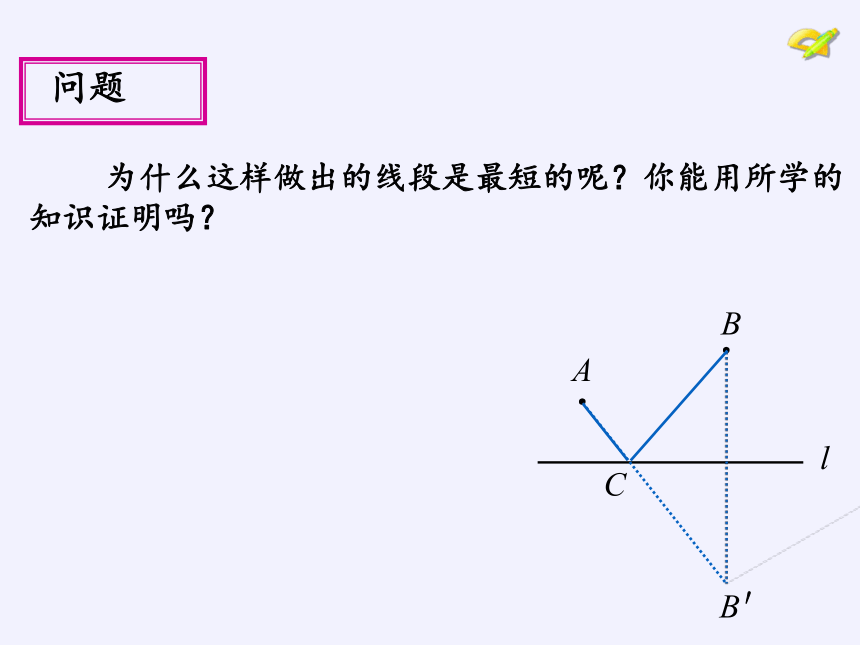
问题
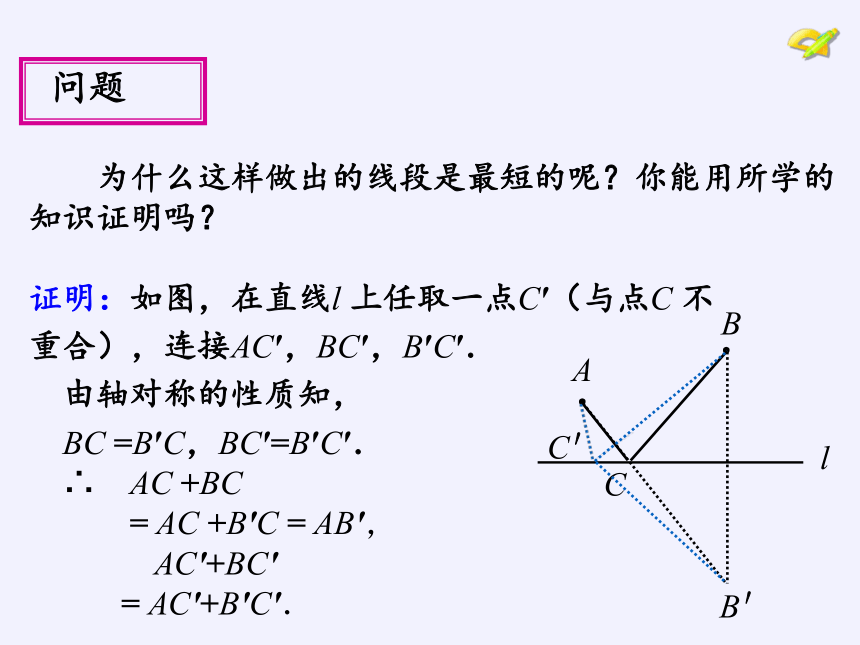
为什么这样做出的线段是最短的呢?你能用所学的知识证明吗?
B
·
l
A
·
B′
C
证明:如图,在直线l 上任取一点C′(与点C 不
重合),连接AC′,BC′,B′C′.
由轴对称的性质知,
BC =B′C,BC′=B′C′.
∴ AC +BC
= AC +B′C = AB′,
AC′+BC′
= AC′+B′C′.
问题
为什么这样做出的线段是最短的呢?你能用所学的知识证明吗?
B
·
l
A
·
B′
C
C′
问题
为什么这样做出的线段是最短的呢?你能用所学的知识证明吗?
B
·
l
A
·
B′
C
C′
证明:在△AB′C′中,
AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
即 AC +BC 最短.
若直线l 上任意一点(与点
C 不重合)与A,B 两点的距离
和都大于AC +BC,就说明AC +
BC 最小.
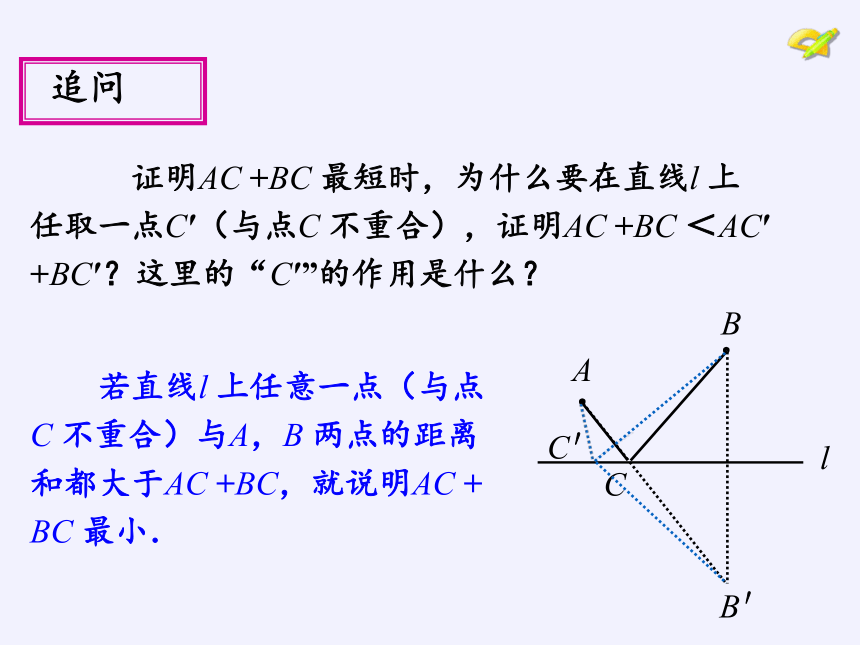
追问
B
·
l
A
·
B′
C
C′
证明AC +BC 最短时,为什么要在直线l 上
任取一点C′(与点C 不重合),证明AC +BC <AC′
+BC′?这里的“C′”的作用是什么?
例2变式:已知:P、Q是△ABC的边AB、
AC上的点,你能在BC上确定一点R,
使△PQR的周长最短吗?
两点在一条直线同侧
(二)一次轴对称:
P`
R
草地
河边
.驻地A
例3.如图:一位将军骑马从驻地A出发,先牵马去草地
OM吃草,再牵马去河边ON喝水, 最后回到驻地A,
问:这位将军怎样走路程最短?
O
M
N
(三):
一点在两相交直线内部
例3变式:已知P是△ABC的边BC上的点,
你能在AB、AC上分别确定一点Q和R,
使△PQR的周长最短吗?
(三):
一点在两相交直线内部
例4:如图,A为马厩,B为帐篷,将军某一天要
从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮助确定这一天的最短路线。
(四):
两点在两相交直线内部
A
B
A/
B/
P
Q
最短路线:A P Q B
l
M
N
例4变式:如图,OMCN是矩形的台球桌面,有黑、白两球分别位于B、A两点的位置上,
试问怎样撞击白球,使白球A依次碰撞球台边OM、ON后,反弹击中黑球?
(四)二次轴对称:
两点在两相交直线内部
.
.
.
.
.
A
A'
B
B'
C
D
M
O
N
例4变式:A、B在直线OM、ON内部,
在OM、ON上分别找点C、D,使四
边形ACDB的周长最小。
(四):
两点在两相交直线内部
小结 将军饮马问题的实质
最短路径问题------
利用轴对称知识确定最短路线:
(1)若动点只有一个,则只需做一次轴对称;
(2)若动点有两个,则需做两次轴对称;
(3)不论做一次轴对称,还是两次轴对称,动点所在的直线就是对称轴。
C
随堂练习:(如图)若城堡A、城堡B
到河岸最短距离分别为AC=1km,BD=2km,
CD=4km,求将军所走的最短路径是多少Km?
A
P
B
A′
D
E
1
2
4
1
1
4
5
小结 将军饮马问题的实质
最短路径问题------
利用轴对称知识确定最短路线:
(1)若动点只有一个,则只需做一次轴对称;
(2)若动点有两个,则需做两次轴对称;
求最短路径通常都需要构造直角三角形,然后用勾股定理进行求解。
综合应用:
著名的恩施大峡谷(A)和世界级自然保护区星斗山(B)位于笔直的沪渝高速公路X同侧,AB=50km,A、B到直线X的距离分别为10km和40km,要在沪渝高速公路旁修建一服务区P,向A、B两景区运送游客.小民设计了两种方案,图11(1)是方案一的示意图(AP与直线X垂直,垂足为P),P到A、B的距离之和S1=PA+PB; 图11(2)是方案二的示意图(点A关于直线X的对称点是A',连接BA'交直线X于点P),P到A、B的距离之和S2=PA+PB.
(1).求S1 、S2 ,并比较它们的大小.
(2).请你说明S2=PA+PB的值为最小.
(3).拟建的恩施到张家界高速公路Y与沪渝高速公路垂直,建立如图所示的直角坐标系,B到直线Y的距离为30km,请你在X,旁和Y旁各修建一服务区P、Q,使P、A、B、Q 组成的四边形的周长最小.并求出这个最小值.
C
Q
10
50
10
30
10
10
40
50
B/
A/
C
30
10
40
50
30
10
小结 将军饮马问题的实质
最短路径问题------
利用轴对称知识确定最短路线:
(1)若动点只有一个,则只需做一次轴对称;
(2)若动点有两个,则需做两次轴对称;
求最短路径通常都需要构造直角三角形,然后用勾股定理进行求解。
谢 谢
将军饮马问题:
早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:
将军每天骑马从城堡A出发,到城堡B,途中
马要到小河边饮水一次。将军问怎样走路程最短?
这就是广为流传的"将军饮马"问题。
P
两点之间线段最短.
根据:
B
A
(一)两点在一条直线两侧
例1.如图:古希腊一位将军骑马从城堡A到城堡B,途中
马要到小溪边饮水一次。问将军怎样走路程最短?
最短路线:
(
分类讨论:
A ---P--- B.
例2.如图:一位将军骑马从城堡A到城堡B, 途中马要到河边饮水一次,问:这位将军怎样走路程最短?
A
B
河
两点在一条直线同侧
(二):
B/
c
例2变式:已知:P、Q是△ABC的边AB、
AC上的点,你能在BC上确定一点R,
使△PQR的周长最短吗?
两点在一条直线同侧
(二)一次轴对称:
p/
R
问题
为什么这样做出的线段是最短的呢?你能用所学的知识证明吗?
B
·
l
A
·
B′
C
证明:如图,在直线l 上任取一点C′(与点C 不
重合),连接AC′,BC′,B′C′.
由轴对称的性质知,
BC =B′C,BC′=B′C′.
∴ AC +BC
= AC +B′C = AB′,
AC′+BC′
= AC′+B′C′.
问题
为什么这样做出的线段是最短的呢?你能用所学的知识证明吗?
B
·
l
A
·
B′
C
C′
问题
为什么这样做出的线段是最短的呢?你能用所学的知识证明吗?
B
·
l
A
·
B′
C
C′
证明:在△AB′C′中,
AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
即 AC +BC 最短.
若直线l 上任意一点(与点
C 不重合)与A,B 两点的距离
和都大于AC +BC,就说明AC +
BC 最小.
追问
B
·
l
A
·
B′
C
C′
证明AC +BC 最短时,为什么要在直线l 上
任取一点C′(与点C 不重合),证明AC +BC <AC′
+BC′?这里的“C′”的作用是什么?
例2变式:已知:P、Q是△ABC的边AB、
AC上的点,你能在BC上确定一点R,
使△PQR的周长最短吗?
两点在一条直线同侧
(二)一次轴对称:
P`
R
草地
河边
.驻地A
例3.如图:一位将军骑马从驻地A出发,先牵马去草地
OM吃草,再牵马去河边ON喝水, 最后回到驻地A,
问:这位将军怎样走路程最短?
O
M
N
(三):
一点在两相交直线内部
例3变式:已知P是△ABC的边BC上的点,
你能在AB、AC上分别确定一点Q和R,
使△PQR的周长最短吗?
(三):
一点在两相交直线内部
例4:如图,A为马厩,B为帐篷,将军某一天要
从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮助确定这一天的最短路线。
(四):
两点在两相交直线内部
A
B
A/
B/
P
Q
最短路线:A P Q B
l
M
N
例4变式:如图,OMCN是矩形的台球桌面,有黑、白两球分别位于B、A两点的位置上,
试问怎样撞击白球,使白球A依次碰撞球台边OM、ON后,反弹击中黑球?
(四)二次轴对称:
两点在两相交直线内部
.
.
.
.
.
A
A'
B
B'
C
D
M
O
N
例4变式:A、B在直线OM、ON内部,
在OM、ON上分别找点C、D,使四
边形ACDB的周长最小。
(四):
两点在两相交直线内部
小结 将军饮马问题的实质
最短路径问题------
利用轴对称知识确定最短路线:
(1)若动点只有一个,则只需做一次轴对称;
(2)若动点有两个,则需做两次轴对称;
(3)不论做一次轴对称,还是两次轴对称,动点所在的直线就是对称轴。
C
随堂练习:(如图)若城堡A、城堡B
到河岸最短距离分别为AC=1km,BD=2km,
CD=4km,求将军所走的最短路径是多少Km?
A
P
B
A′
D
E
1
2
4
1
1
4
5
小结 将军饮马问题的实质
最短路径问题------
利用轴对称知识确定最短路线:
(1)若动点只有一个,则只需做一次轴对称;
(2)若动点有两个,则需做两次轴对称;
求最短路径通常都需要构造直角三角形,然后用勾股定理进行求解。
综合应用:
著名的恩施大峡谷(A)和世界级自然保护区星斗山(B)位于笔直的沪渝高速公路X同侧,AB=50km,A、B到直线X的距离分别为10km和40km,要在沪渝高速公路旁修建一服务区P,向A、B两景区运送游客.小民设计了两种方案,图11(1)是方案一的示意图(AP与直线X垂直,垂足为P),P到A、B的距离之和S1=PA+PB; 图11(2)是方案二的示意图(点A关于直线X的对称点是A',连接BA'交直线X于点P),P到A、B的距离之和S2=PA+PB.
(1).求S1 、S2 ,并比较它们的大小.
(2).请你说明S2=PA+PB的值为最小.
(3).拟建的恩施到张家界高速公路Y与沪渝高速公路垂直,建立如图所示的直角坐标系,B到直线Y的距离为30km,请你在X,旁和Y旁各修建一服务区P、Q,使P、A、B、Q 组成的四边形的周长最小.并求出这个最小值.
C
Q
10
50
10
30
10
10
40
50
B/
A/
C
30
10
40
50
30
10
小结 将军饮马问题的实质
最短路径问题------
利用轴对称知识确定最短路线:
(1)若动点只有一个,则只需做一次轴对称;
(2)若动点有两个,则需做两次轴对称;
求最短路径通常都需要构造直角三角形,然后用勾股定理进行求解。
谢 谢
