冀教版八年级上册 数学 课件: 17.3勾股定理1(21张)
文档属性
| 名称 | 冀教版八年级上册 数学 课件: 17.3勾股定理1(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 23:10:45 | ||
图片预览



文档简介
勾股定理
B
A
C
b
a
c
直角三角形三边关系
一、 猜想
a、b、c之间的关系
?
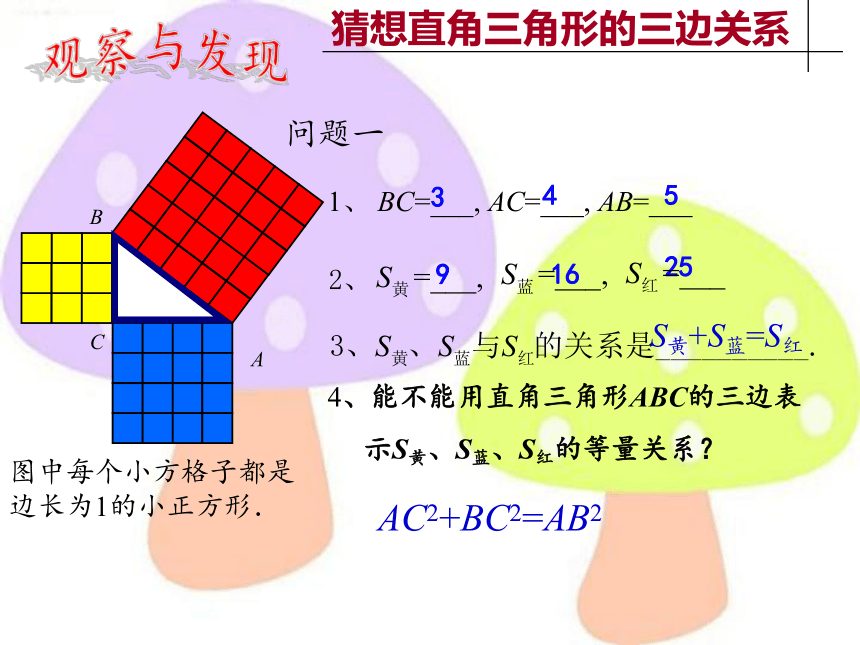
观察与发现
3
5
4
9
16
25
问题一
1、 BC=___, AC=___, AB=___
2、
猜想直角三角形的三边关系
4、能不能用直角三角形ABC的三边表
示S黄、S蓝、S红的等量关系?
S黄+S蓝=S红
AC2+BC2=AB2
图中每个小方格子都是边长为1的小正方形.
B
C
A
B
C
A
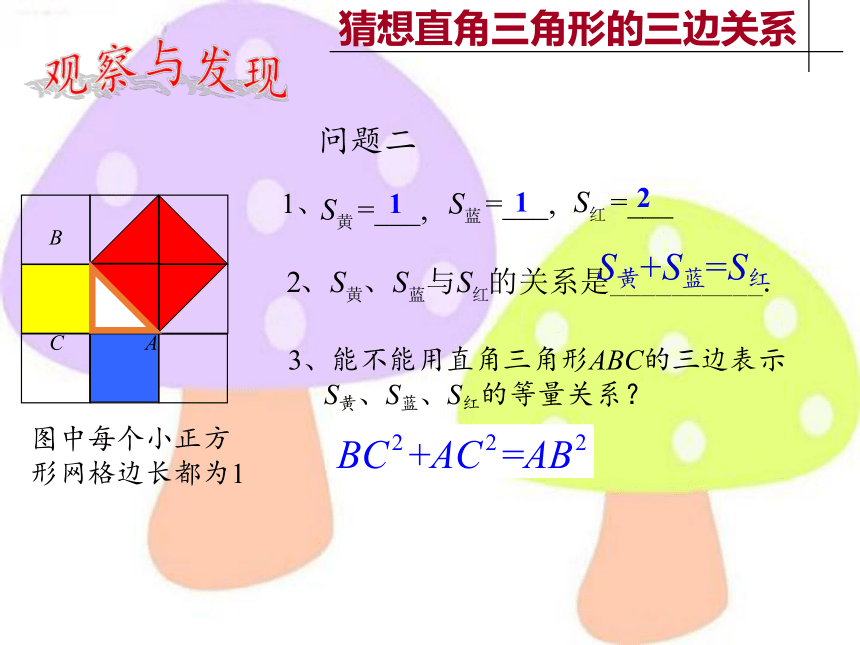
图中每个小正方形网格边长都为1
猜想直角三角形的三边关系
观察与发现
1
2
1
1、
问题二
S黄+S蓝=S红
3、能不能用直角三角形ABC的三边表示
S黄、S蓝、S红的等量关系?
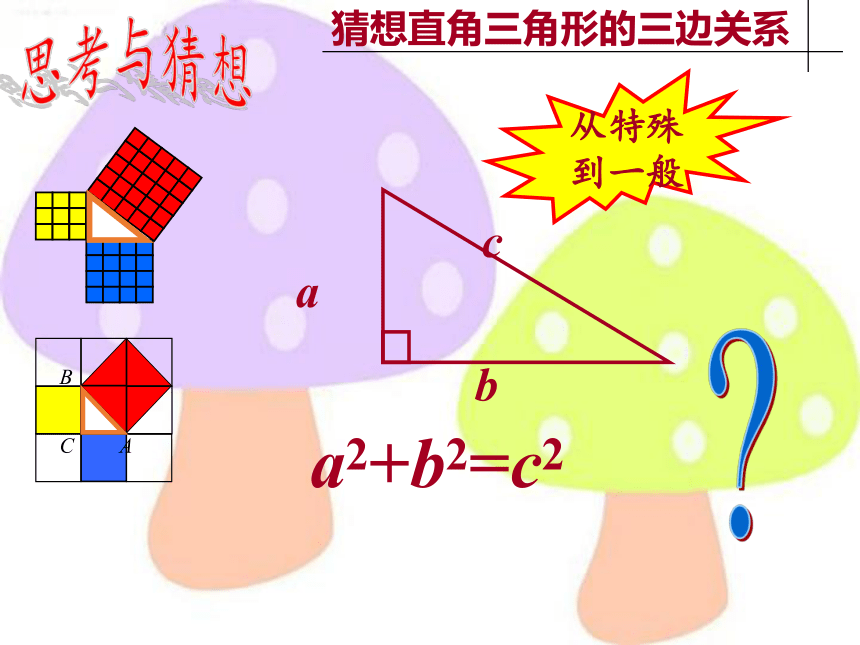
思考与猜想
猜想直角三角形的三边关系
a2+b2=c2
?
a
b
c
B
C
A
从特殊
到一般
B
A
C
b
a
c
直角三角形三边关系
二、 验证
a2+b2=c2
?
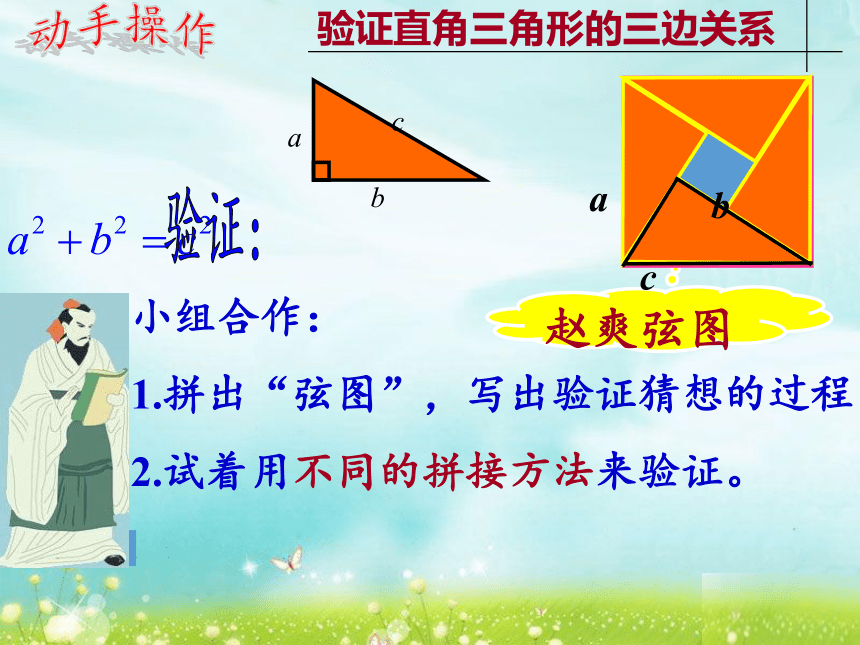
动手操作
验证直角三角形的三边关系
小组合作:
1.拼出“弦图”,写出验证猜想的过程;
2.试着用不同的拼接方法来验证。
赵爽弦图
b
a
c
验证:
a
b
c
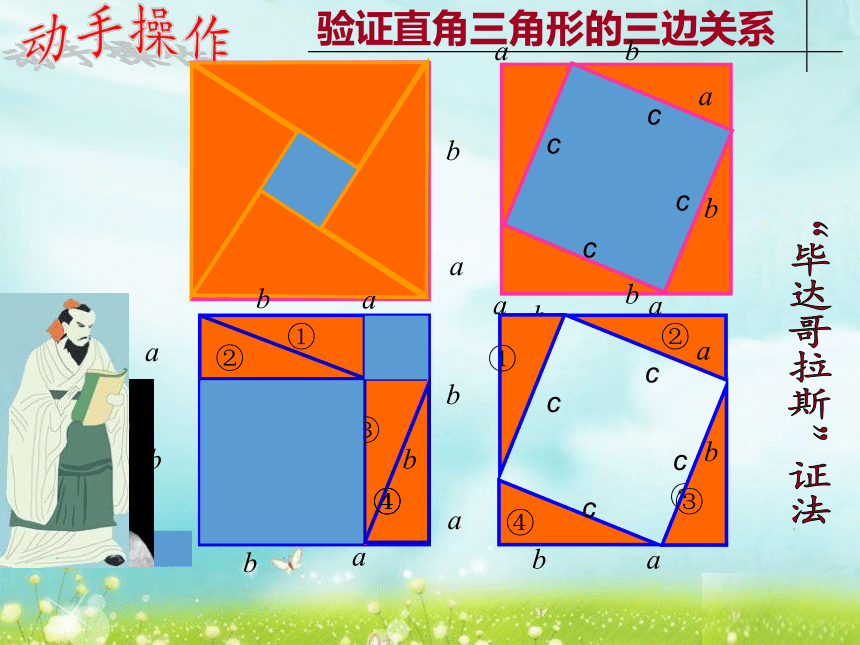
动手操作
验证直角三角形的三边关系
a
a
a
a
b
b
b
b
c
c
c
c
a
a
a
a
b
b
b
b
①
④
②
③
④
③
①
②
④
c
c
c
c
②
③
b
b
b
b
a
a
a
a
“毕达哥拉斯”证法
动手操作
验证直角三角形的三边关系
“总统证法”
数形结合
A
B
C
∴ ______________
( AB2 - AC2=BC2 ;
AB2 - BC2=AC2 )
∵ _____________
在△ABC中,
验证直角三角形的三边关系
勾股定理
符号语言:
如果直角三角形两直角边分别为a、b、斜边为c,那么 .
∵∠ACB= 90°
∴ AC2+BC2 =AB2
验证直角三角形的三边关系
勾
股
勾
股
弦
较短的直角边
较长的直角边
斜边
勾股定理
如果直角三角形两直角边分别为a、b、斜边为c,那么 .
B
A
C
b
a
c
直角三角形的三边关系
三、 应用
a2+b2=c2
3
4
5
1.求下面各直角三角形中未知的边长.
C
A
B
基础闯关
巩固与应用
在直角三角形 ABC中,∠C=90°,a=3,b=4, c=_______.
巩固与应用
基础闯关
5
在直角三角形 ABC中,a=3,
b=4, c=__________.
变式训练
分类讨论
3
4
C
A
B
善于思考的王明说:任意两个正方形,它们的面积和,一定等于某一个正方形的面积,你认为王明说的有道理吗?说明你的理由。
3.2拓展提升
+
=
?
挑战自我
?
挑战自我
回顾与反思
现实情境
猜 想
验 证
得到定理
巩固应用
知识的形成
1、 知识上……
2、方法上……
——让我们的认识升华
我来答!
深化理解
作业
选做题:
同学们课下查阅资料,写一篇关于勾股定理证明方法的小论文。
必做题:
课本P152,习题1、2、3.
感谢同学们和我一起度过快乐的一节课!
谢 谢
B
A
C
b
a
c
直角三角形三边关系
一、 猜想
a、b、c之间的关系
?
观察与发现
3
5
4
9
16
25
问题一
1、 BC=___, AC=___, AB=___
2、
猜想直角三角形的三边关系
4、能不能用直角三角形ABC的三边表
示S黄、S蓝、S红的等量关系?
S黄+S蓝=S红
AC2+BC2=AB2
图中每个小方格子都是边长为1的小正方形.
B
C
A
B
C
A
图中每个小正方形网格边长都为1
猜想直角三角形的三边关系
观察与发现
1
2
1
1、
问题二
S黄+S蓝=S红
3、能不能用直角三角形ABC的三边表示
S黄、S蓝、S红的等量关系?
思考与猜想
猜想直角三角形的三边关系
a2+b2=c2
?
a
b
c
B
C
A
从特殊
到一般
B
A
C
b
a
c
直角三角形三边关系
二、 验证
a2+b2=c2
?
动手操作
验证直角三角形的三边关系
小组合作:
1.拼出“弦图”,写出验证猜想的过程;
2.试着用不同的拼接方法来验证。
赵爽弦图
b
a
c
验证:
a
b
c
动手操作
验证直角三角形的三边关系
a
a
a
a
b
b
b
b
c
c
c
c
a
a
a
a
b
b
b
b
①
④
②
③
④
③
①
②
④
c
c
c
c
②
③
b
b
b
b
a
a
a
a
“毕达哥拉斯”证法
动手操作
验证直角三角形的三边关系
“总统证法”
数形结合
A
B
C
∴ ______________
( AB2 - AC2=BC2 ;
AB2 - BC2=AC2 )
∵ _____________
在△ABC中,
验证直角三角形的三边关系
勾股定理
符号语言:
如果直角三角形两直角边分别为a、b、斜边为c,那么 .
∵∠ACB= 90°
∴ AC2+BC2 =AB2
验证直角三角形的三边关系
勾
股
勾
股
弦
较短的直角边
较长的直角边
斜边
勾股定理
如果直角三角形两直角边分别为a、b、斜边为c,那么 .
B
A
C
b
a
c
直角三角形的三边关系
三、 应用
a2+b2=c2
3
4
5
1.求下面各直角三角形中未知的边长.
C
A
B
基础闯关
巩固与应用
在直角三角形 ABC中,∠C=90°,a=3,b=4, c=_______.
巩固与应用
基础闯关
5
在直角三角形 ABC中,a=3,
b=4, c=__________.
变式训练
分类讨论
3
4
C
A
B
善于思考的王明说:任意两个正方形,它们的面积和,一定等于某一个正方形的面积,你认为王明说的有道理吗?说明你的理由。
3.2拓展提升
+
=
?
挑战自我
?
挑战自我
回顾与反思
现实情境
猜 想
验 证
得到定理
巩固应用
知识的形成
1、 知识上……
2、方法上……
——让我们的认识升华
我来答!
深化理解
作业
选做题:
同学们课下查阅资料,写一篇关于勾股定理证明方法的小论文。
必做题:
课本P152,习题1、2、3.
感谢同学们和我一起度过快乐的一节课!
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
