冀教版九年级上册 数学 课件: 26.4 解直角三角形的应用1(16张)
文档属性
| 名称 | 冀教版九年级上册 数学 课件: 26.4 解直角三角形的应用1(16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 255.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 23:16:04 | ||
图片预览




文档简介
1.在解直角三角形时,除直角外还有5个元素,至少知道几个元素才能求出其他的元素?
A
B
a
b
c
C
回顾:
回顾:
2.除直角外的5个元素有哪些
关系?
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
a2+b2=c2
在解直角三角形的过程中,一般要用到的一些关系:
回顾:
解直角三角形及其应用:
--仰角俯角问题
1.理解仰角俯角的定义,并会用相关知识解决仰角俯角的问题.
2.将实际问题抽象为数学问题,建立起与解直角三角形知识有关的数学模型,培养学生的分析问题,解决问题的能力.
学习目标
A
B
C
6
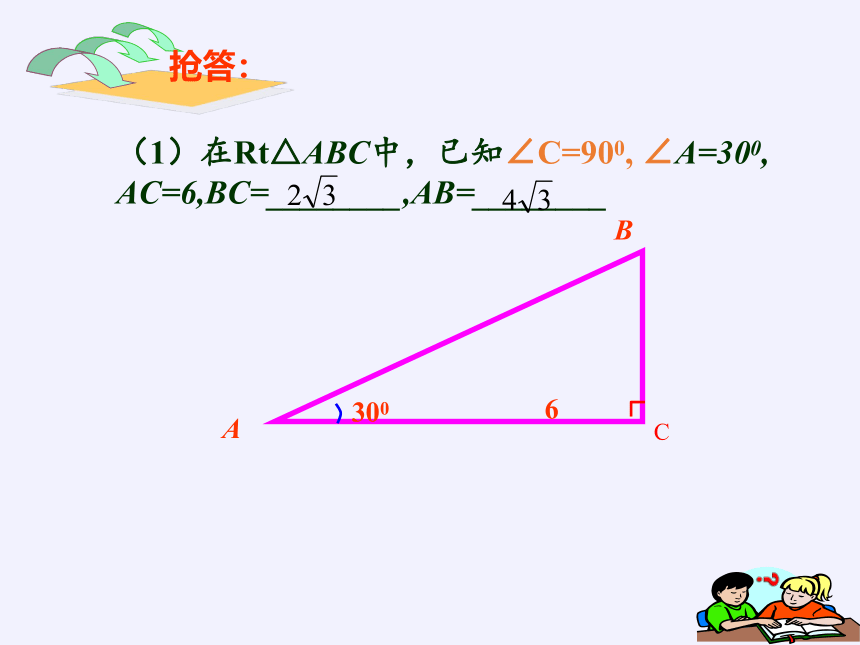
抢答:
(1)在Rt△ABC中,已知∠C=900, ∠A=300,
AC=6,BC=________,AB=________
300
A
B
C
6
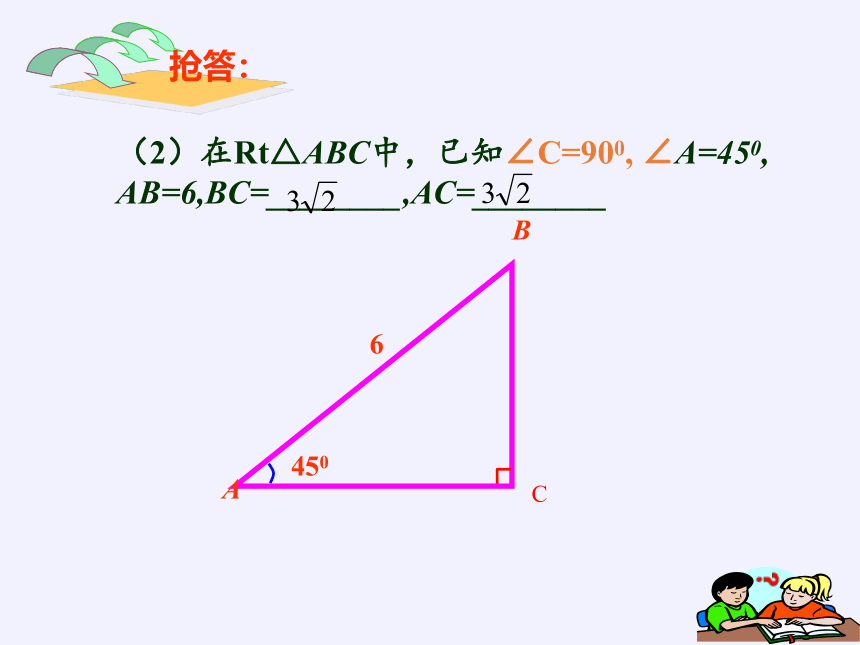
抢答:
(2)在Rt△ABC中,已知∠C=900, ∠A=450,
AB=6,BC=________,AC=________
450
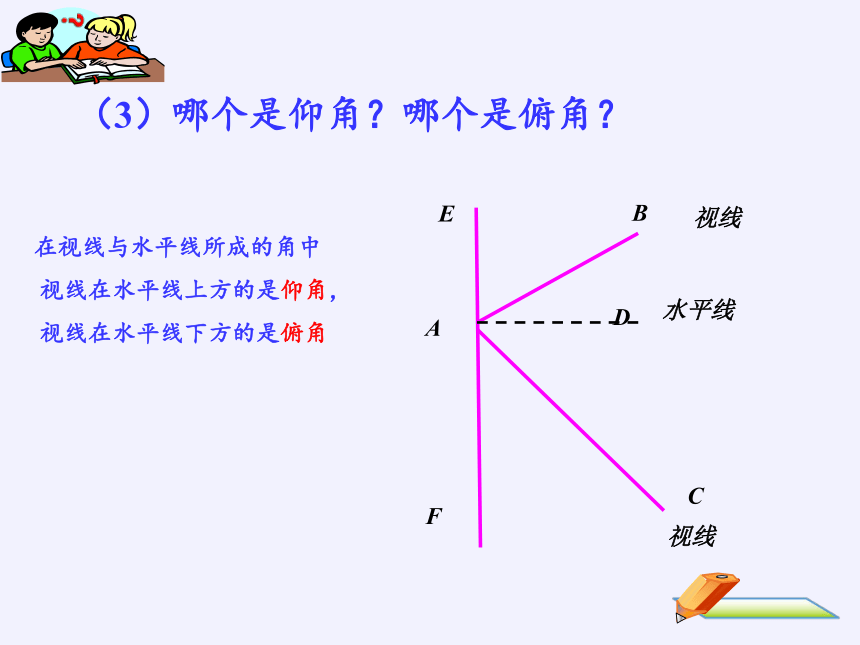
在视线与水平线所成的角中
视线在水平线上方的是仰角,
视线在水平线下方的是俯角
(3)哪个是仰角?哪个是俯角?
A
B
C
D
视线
视线
水平线
F
E
例:某数学兴趣小组设计了一个测量实验:已知教学楼的AD高9米,小亮在楼顶的D处测得点B的俯角为60 °,测得点C的俯角为30 °,求BC的长.(结果保留根号)
例题解析:
C
D
A
B
E
解:由题可得, ∠ EDB= 60°,∠ EDC = 30°
答: BC的长是 米。
C
D
A
B
E
∴ ∠ ADB= 30°, ∠ ADC= 60°
在Rt△ ADC中
在Rt△ ADB中
解:由题可得, ∠ EDB= 60°,∠ EDC = 30°
答: BC的长是 米。
C
D
A
B
E
∴ ∠ CDB=∠ C= ∠ ADB= 30°
∴BC=BD
在Rt△ ADB中
归
纳
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三
角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
(变式)某数学兴趣小组设计了一个测量实验:已知BC之间的距离为6米,小亮在楼顶的D处测得点B的俯角为45 °,测得点C的俯角为30 °,求教学楼AD的高(结果保留根号)
变式训练:
C
D
A
B
E
(河南2014-19):在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为300,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为680.试根据以上数据求出潜艇离开海平面的下潜深度.(结果保留整数.参考数据sin680 ≈ 0.9,cos680 ≈ 0.4,tan680 ≈ 2.5)
链接中考:
海平面
B
C
680
A
300
D
小结 拓展
这节课你有什么收获?
(河南2015-20):如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是300,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是480.若∠FAE=300,求大树的高度.(结果保留整数.参考数据sin480 ≈ 0.74,cos480 ≈ 0.67,tan480 ≈ 1.11)
E
挑战自我:
G
M
H
谢 谢
A
B
a
b
c
C
回顾:
回顾:
2.除直角外的5个元素有哪些
关系?
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
a2+b2=c2
在解直角三角形的过程中,一般要用到的一些关系:
回顾:
解直角三角形及其应用:
--仰角俯角问题
1.理解仰角俯角的定义,并会用相关知识解决仰角俯角的问题.
2.将实际问题抽象为数学问题,建立起与解直角三角形知识有关的数学模型,培养学生的分析问题,解决问题的能力.
学习目标
A
B
C
6
抢答:
(1)在Rt△ABC中,已知∠C=900, ∠A=300,
AC=6,BC=________,AB=________
300
A
B
C
6
抢答:
(2)在Rt△ABC中,已知∠C=900, ∠A=450,
AB=6,BC=________,AC=________
450
在视线与水平线所成的角中
视线在水平线上方的是仰角,
视线在水平线下方的是俯角
(3)哪个是仰角?哪个是俯角?
A
B
C
D
视线
视线
水平线
F
E
例:某数学兴趣小组设计了一个测量实验:已知教学楼的AD高9米,小亮在楼顶的D处测得点B的俯角为60 °,测得点C的俯角为30 °,求BC的长.(结果保留根号)
例题解析:
C
D
A
B
E
解:由题可得, ∠ EDB= 60°,∠ EDC = 30°
答: BC的长是 米。
C
D
A
B
E
∴ ∠ ADB= 30°, ∠ ADC= 60°
在Rt△ ADC中
在Rt△ ADB中
解:由题可得, ∠ EDB= 60°,∠ EDC = 30°
答: BC的长是 米。
C
D
A
B
E
∴ ∠ CDB=∠ C= ∠ ADB= 30°
∴BC=BD
在Rt△ ADB中
归
纳
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三
角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
(变式)某数学兴趣小组设计了一个测量实验:已知BC之间的距离为6米,小亮在楼顶的D处测得点B的俯角为45 °,测得点C的俯角为30 °,求教学楼AD的高(结果保留根号)
变式训练:
C
D
A
B
E
(河南2014-19):在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为300,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为680.试根据以上数据求出潜艇离开海平面的下潜深度.(结果保留整数.参考数据sin680 ≈ 0.9,cos680 ≈ 0.4,tan680 ≈ 2.5)
链接中考:
海平面
B
C
680
A
300
D
小结 拓展
这节课你有什么收获?
(河南2015-20):如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是300,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是480.若∠FAE=300,求大树的高度.(结果保留整数.参考数据sin480 ≈ 0.74,cos480 ≈ 0.67,tan480 ≈ 1.11)
E
挑战自我:
G
M
H
谢 谢
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
