冀教版九年级上册 数学 课件: 28.2 过三点的圆(22张)
文档属性
| 名称 | 冀教版九年级上册 数学 课件: 28.2 过三点的圆(22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 267.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 00:00:00 | ||
图片预览




文档简介
28.2 过三点的圆
1.复习并巩固圆中的基本概念.
2.理解并掌握三点确定圆的条件并会应用. (重点)
3.理解并掌握三角形的外接圆及外心的概念.(难点)
学习目标
唐朝的铜镜是中国铜镜中的精品。江西省文物考古研究所日前从玉山县一座唐代墓葬中出土了半面铜镜,那么你有什么方法使得它能“破镜重圆”呢?
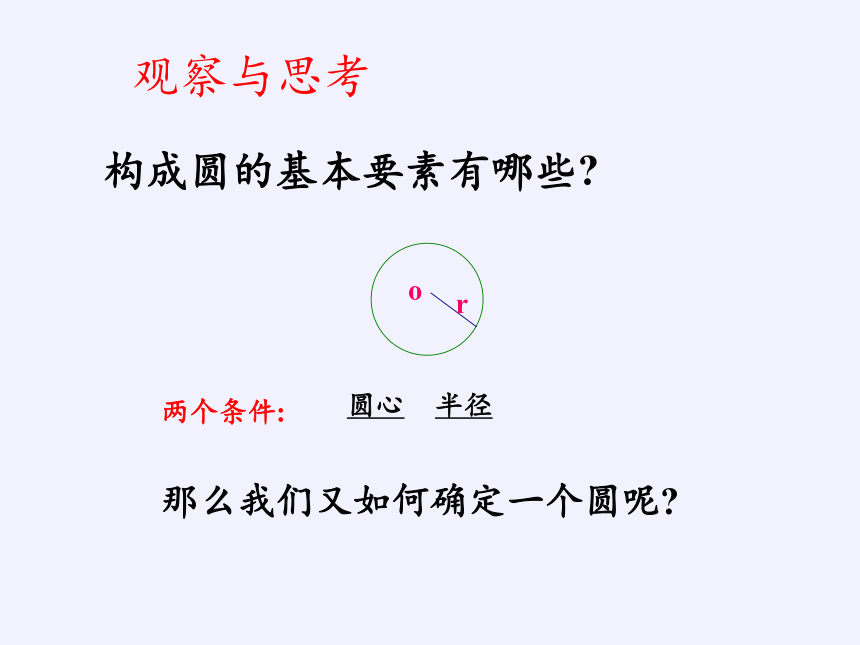
构成圆的基本要素有哪些?
观察与思考
o
r
两个条件:
圆心
半径
那么我们又如何确定一个圆呢?
●A
●A
●B
过一点可作几条直线?过两点可以作几条直线?过三点呢?
过两点有且只有一条直线
(“有且只有”就是“确定”的意思)
经过一点可以作无数条直线;
回忆思考:
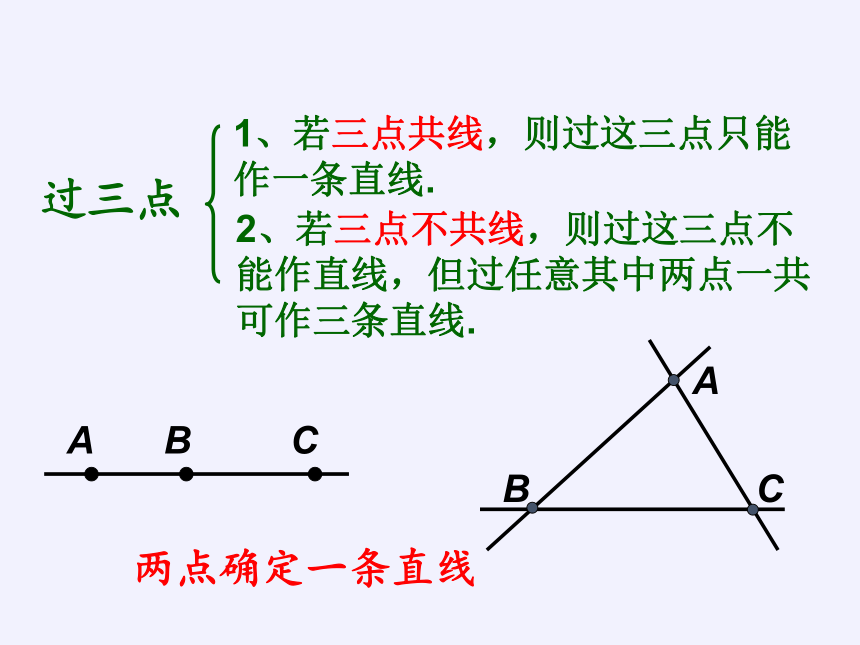
过三点
1、若三点共线,则过这三点只能作一条直线.
A
B
C
2、若三点不共线,则过这三点不能作直线,但过任意其中两点一共可作三条直线.
A
B
C
两点确定一条直线
对于一个圆来说,过几个点能作一个圆,并且只能作一个圆?
类比探究:
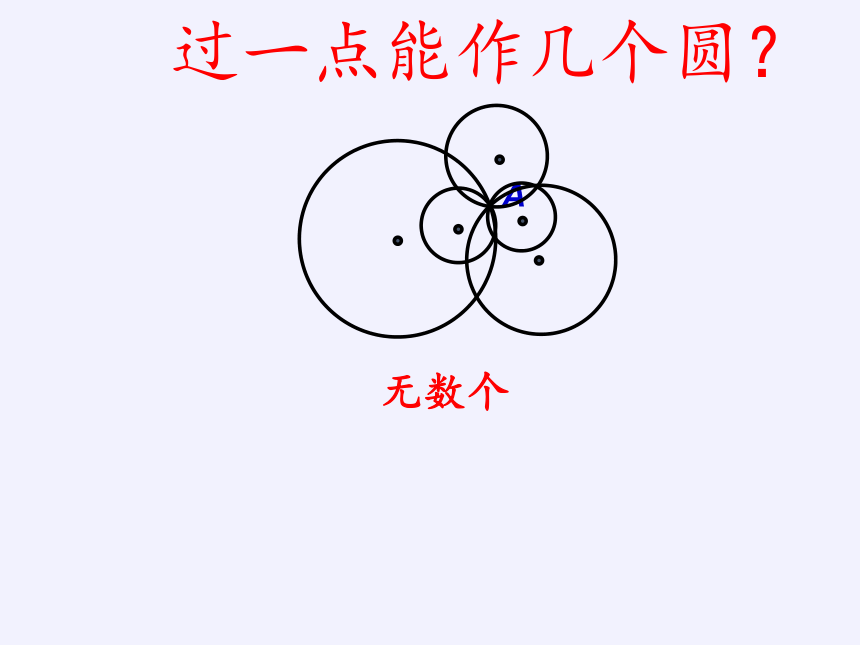
过一点能作几个圆?
无数个
A
过两点能作几个圆?
A
B
过A、B两点的圆的圆心有何特点?
经过两点A、B的圆有无数个
经过两点A、B的圆的圆心在线段AB的垂直平分线上.
A
B
C
为什么过同一直线上的三点不能作圆呢?
因为DE∥FG,所以没有交点,
即没有过这三点的圆心
D
F
E
G
过三点能作几个圆?
1.三点共线
(不能作圆)
1、连结AB,作线段AB的垂直平分线DE;
2、连结BC,作线段BC的垂直平分线FG,交DE于点O;
3、以O为圆心,OB为半径作圆。
作法:
A
B
C
O
D
E
G
F
⊙O就是所求作的圆。
已知:不在同一直线上的三点 A、B、C
求作:⊙O,使它经过A、B、C
2、三点不共线
不在同一直线上的三点确定一个圆
O
A
B
C
归纳
O
1.由以上归纳可知:经过三角形三个顶点可以作一个圆.并且只能作一个圆。
2.经过三角形各顶点的圆叫做三角形的外接圆;这个三角形叫做圆的内接三角形。
3.三角形外接圆的圆心叫做三角形的外心。
A
B
C
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
外心
1.三边垂直平分线的交点
2.到三个顶点的距离相等
课堂练习
判断题:
1、过三点一定可以作圆 ( )
2、一个三角形有且只有一个外接圆 ( )
3、任意一个圆有一个内接三角形,并且只有一个内接三角形 ( )
4、三角形的外心就是这个三角形任意两边垂直平分线的交点 ( )
5、三角形的外心到三边的距离相等 ( )
错
对
错
对
错
O
A
B
C
A
B
C
O
直角三角形外心是斜边AB的中点
钝角三角形外心在△ABC的外部
三角形的外心是否一定在三角形的内部?
你强,我更强!
1. 如果直角三角形的两条直角边分别是6和8,你能求出这个直角三角形外接圆的半径吗?是多少?
2.如果直角三角形的两条边分别是6和8,你能求出这个直角三角形外接圆的半径吗?是多少?
如何解决“破镜重圆”的问题?
A
B
C
O
我学会了什么 ?
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定;
(2)经过一个已知点能作无数个圆;
(3)经过两个已知点A、B能作无数个圆,这些圆的圆心在线段AB的垂直平分线上;
(4)不在同一直线上的三个点确定一个圆;
(5)经过三角形的三个顶点的圆叫做三角形的外接圆;外接圆的圆心叫三角形的外心;这个三角形叫做圆的内接三角形.
为美化校园,学校要把一块三角形空地扩建成一个圆形喷水池,在三角形三个顶点处各有一棵名贵花树(A、B、C),若不动花树,还要建一个最大的圆形喷水池,请设计你的实施方案。
C
B
A
?
谢 谢
1.复习并巩固圆中的基本概念.
2.理解并掌握三点确定圆的条件并会应用. (重点)
3.理解并掌握三角形的外接圆及外心的概念.(难点)
学习目标
唐朝的铜镜是中国铜镜中的精品。江西省文物考古研究所日前从玉山县一座唐代墓葬中出土了半面铜镜,那么你有什么方法使得它能“破镜重圆”呢?
构成圆的基本要素有哪些?
观察与思考
o
r
两个条件:
圆心
半径
那么我们又如何确定一个圆呢?
●A
●A
●B
过一点可作几条直线?过两点可以作几条直线?过三点呢?
过两点有且只有一条直线
(“有且只有”就是“确定”的意思)
经过一点可以作无数条直线;
回忆思考:
过三点
1、若三点共线,则过这三点只能作一条直线.
A
B
C
2、若三点不共线,则过这三点不能作直线,但过任意其中两点一共可作三条直线.
A
B
C
两点确定一条直线
对于一个圆来说,过几个点能作一个圆,并且只能作一个圆?
类比探究:
过一点能作几个圆?
无数个
A
过两点能作几个圆?
A
B
过A、B两点的圆的圆心有何特点?
经过两点A、B的圆有无数个
经过两点A、B的圆的圆心在线段AB的垂直平分线上.
A
B
C
为什么过同一直线上的三点不能作圆呢?
因为DE∥FG,所以没有交点,
即没有过这三点的圆心
D
F
E
G
过三点能作几个圆?
1.三点共线
(不能作圆)
1、连结AB,作线段AB的垂直平分线DE;
2、连结BC,作线段BC的垂直平分线FG,交DE于点O;
3、以O为圆心,OB为半径作圆。
作法:
A
B
C
O
D
E
G
F
⊙O就是所求作的圆。
已知:不在同一直线上的三点 A、B、C
求作:⊙O,使它经过A、B、C
2、三点不共线
不在同一直线上的三点确定一个圆
O
A
B
C
归纳
O
1.由以上归纳可知:经过三角形三个顶点可以作一个圆.并且只能作一个圆。
2.经过三角形各顶点的圆叫做三角形的外接圆;这个三角形叫做圆的内接三角形。
3.三角形外接圆的圆心叫做三角形的外心。
A
B
C
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
外心
1.三边垂直平分线的交点
2.到三个顶点的距离相等
课堂练习
判断题:
1、过三点一定可以作圆 ( )
2、一个三角形有且只有一个外接圆 ( )
3、任意一个圆有一个内接三角形,并且只有一个内接三角形 ( )
4、三角形的外心就是这个三角形任意两边垂直平分线的交点 ( )
5、三角形的外心到三边的距离相等 ( )
错
对
错
对
错
O
A
B
C
A
B
C
O
直角三角形外心是斜边AB的中点
钝角三角形外心在△ABC的外部
三角形的外心是否一定在三角形的内部?
你强,我更强!
1. 如果直角三角形的两条直角边分别是6和8,你能求出这个直角三角形外接圆的半径吗?是多少?
2.如果直角三角形的两条边分别是6和8,你能求出这个直角三角形外接圆的半径吗?是多少?
如何解决“破镜重圆”的问题?
A
B
C
O
我学会了什么 ?
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定;
(2)经过一个已知点能作无数个圆;
(3)经过两个已知点A、B能作无数个圆,这些圆的圆心在线段AB的垂直平分线上;
(4)不在同一直线上的三个点确定一个圆;
(5)经过三角形的三个顶点的圆叫做三角形的外接圆;外接圆的圆心叫三角形的外心;这个三角形叫做圆的内接三角形.
为美化校园,学校要把一块三角形空地扩建成一个圆形喷水池,在三角形三个顶点处各有一棵名贵花树(A、B、C),若不动花树,还要建一个最大的圆形喷水池,请设计你的实施方案。
C
B
A
?
谢 谢
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
