沪科版七年级上册 数学 课件 :1.5 有理数的乘除(14张)
文档属性
| 名称 | 沪科版七年级上册 数学 课件 :1.5 有理数的乘除(14张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 160.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 07:00:54 | ||
图片预览





文档简介
1.5 有理数的乘除
引入
我们已经学过两个正有理数相乘,以及一个正有理数和0相乘。
如 (+2) ×(+3) = 6
(+2) ×0 = 0
如果两个有理数相乘,其中有负数时,应该怎么办呢?
问题1:森林里住着一只蜗牛(在0点处),每天都要离开家去寻找食物,如果蜗牛一直以每分钟2cm 的速度向右爬行,那么3分钟后蜗牛在什么位置?
-2
0
2
4
6
8
3分钟后蜗牛应在0点的右边6cm处。
可以表示为:(+2)×(+3) =+6
规定:向右为正,现在之后为正。
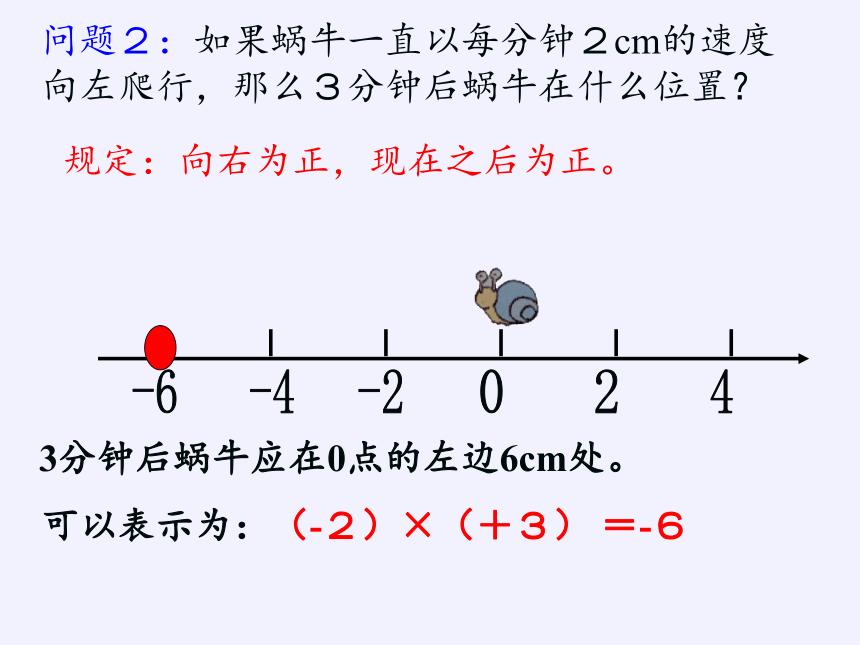
问题2:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后蜗牛在什么位置?
-6
-4
-2
0
2
4
3分钟后蜗牛应在0点的左边6cm处。
可以表示为:(-2)×(+3) =-6
规定:向右为正,现在之后为正。
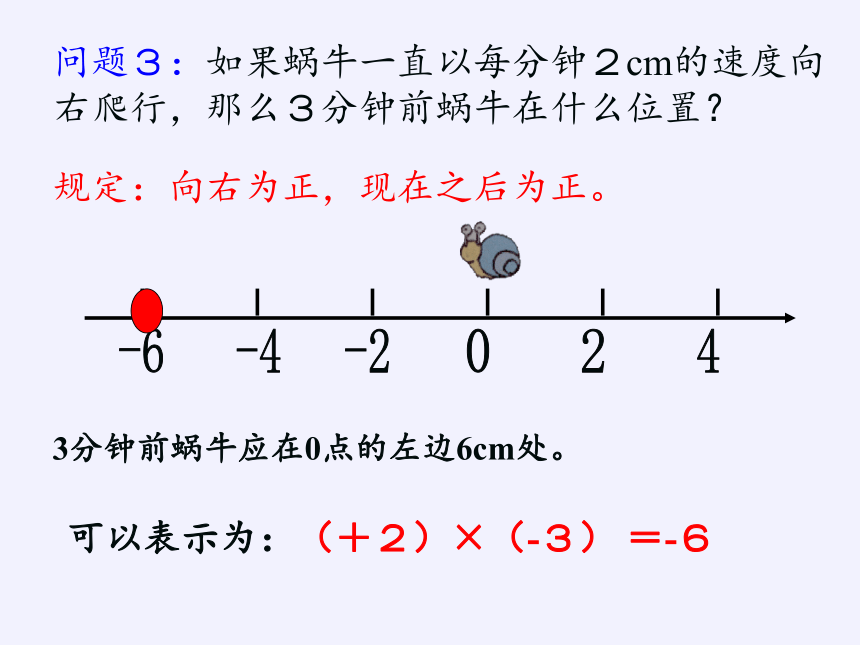
问题3:如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟前蜗牛在什么位置?
-6
-4
-2
0
2
4
3分钟前蜗牛应在0点的左边6cm处。
可以表示为:(+2)×(-3) =-6
规定:向右为正,现在之后为正。
问题4:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟前蜗牛在什么位置?
-2
0
2
4
6
8
3分钟前蜗牛应在0点的右边6cm处。
可以表示为:(-2)×(-3) =+6
规定:向右为正,现在之后为正。
观察这四个式子:
(+2)×(+3)=+6
(-2)×(+3)=-6
(+2)×(-3)=-6
(-2)×(-3)=+6
你有什么发现吗?
(+2)×(+3)=+6
(-2)×(-3)=+6
(-2)×(+3)=-6
(+2)×(-3)=-6
根据你对有理数乘法的思考,总结填空:
正数乘正数,积为__数,
负数乘负数,积为__数;
负数乘正数,积为__数,
正数乘负数,积为__数。
乘积的绝对值等于各乘数绝对值的_____。
积
同号得正
异号得负
}
}
正
正
负
负
思考:当一个因数为0时,积是多少?
任何数和0相乘都得0.
你能总结有理数乘法的计算法则吗?
有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘。
2.任何数同0相乘,都得0。
例1 计算
(1)(-5)×(-6) (2) (- )×
(3)(- )×(- ) (4)8×(-1.25)
解
(1)(-5)×(-6)= +(5×6)= 30
(2)(- )× = -( × )= -
(3)(- )×(- )= +( × )=1
(4)8×(-1.25)=-(8×1.25)=-10
观察上面第(3)个算式,你发现了什么?
如果两个有理数的乘积是1,我们就说这两个数互为倒数。
(- )和(- )互为倒数。
你学到了什么?
谢 谢
引入
我们已经学过两个正有理数相乘,以及一个正有理数和0相乘。
如 (+2) ×(+3) = 6
(+2) ×0 = 0
如果两个有理数相乘,其中有负数时,应该怎么办呢?
问题1:森林里住着一只蜗牛(在0点处),每天都要离开家去寻找食物,如果蜗牛一直以每分钟2cm 的速度向右爬行,那么3分钟后蜗牛在什么位置?
-2
0
2
4
6
8
3分钟后蜗牛应在0点的右边6cm处。
可以表示为:(+2)×(+3) =+6
规定:向右为正,现在之后为正。
问题2:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后蜗牛在什么位置?
-6
-4
-2
0
2
4
3分钟后蜗牛应在0点的左边6cm处。
可以表示为:(-2)×(+3) =-6
规定:向右为正,现在之后为正。
问题3:如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟前蜗牛在什么位置?
-6
-4
-2
0
2
4
3分钟前蜗牛应在0点的左边6cm处。
可以表示为:(+2)×(-3) =-6
规定:向右为正,现在之后为正。
问题4:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟前蜗牛在什么位置?
-2
0
2
4
6
8
3分钟前蜗牛应在0点的右边6cm处。
可以表示为:(-2)×(-3) =+6
规定:向右为正,现在之后为正。
观察这四个式子:
(+2)×(+3)=+6
(-2)×(+3)=-6
(+2)×(-3)=-6
(-2)×(-3)=+6
你有什么发现吗?
(+2)×(+3)=+6
(-2)×(-3)=+6
(-2)×(+3)=-6
(+2)×(-3)=-6
根据你对有理数乘法的思考,总结填空:
正数乘正数,积为__数,
负数乘负数,积为__数;
负数乘正数,积为__数,
正数乘负数,积为__数。
乘积的绝对值等于各乘数绝对值的_____。
积
同号得正
异号得负
}
}
正
正
负
负
思考:当一个因数为0时,积是多少?
任何数和0相乘都得0.
你能总结有理数乘法的计算法则吗?
有理数乘法法则
1.两数相乘,同号得正,异号得负,并把绝对值相乘。
2.任何数同0相乘,都得0。
例1 计算
(1)(-5)×(-6) (2) (- )×
(3)(- )×(- ) (4)8×(-1.25)
解
(1)(-5)×(-6)= +(5×6)= 30
(2)(- )× = -( × )= -
(3)(- )×(- )= +( × )=1
(4)8×(-1.25)=-(8×1.25)=-10
观察上面第(3)个算式,你发现了什么?
如果两个有理数的乘积是1,我们就说这两个数互为倒数。
(- )和(- )互为倒数。
你学到了什么?
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
