沪科版七年级上册 数学 课件 :1.6 有理数的乘方(23张)
文档属性
| 名称 | 沪科版七年级上册 数学 课件 :1.6 有理数的乘方(23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 07:03:00 | ||
图片预览



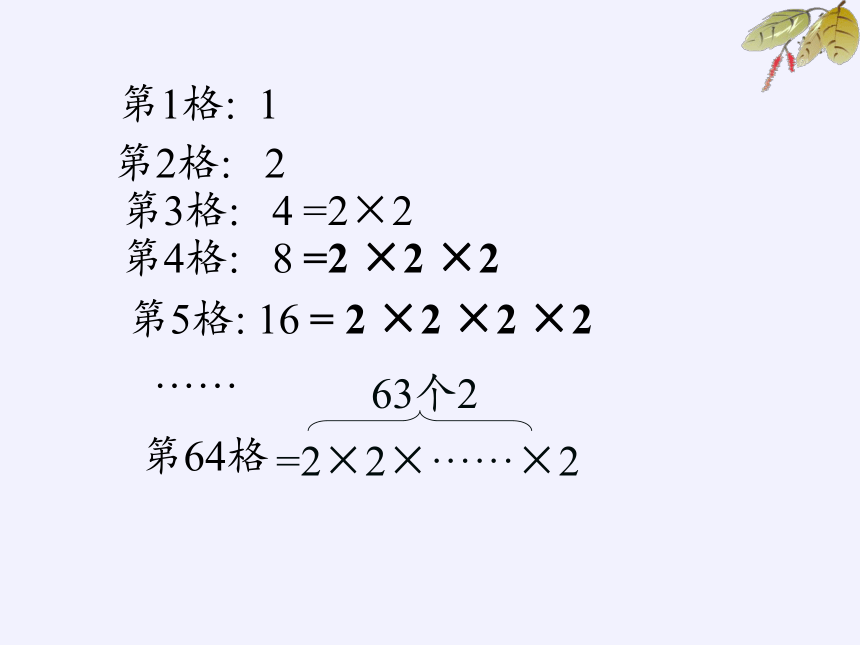




文档简介
1.6 有理数的乘方
棋盘上的学问
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,就在这个棋盘上放一些米粒吧!第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
你认为国王的国库里有这么多米吗?
第64格
第1格: 1
第2格: 2
第3格: 4
=2×2
第4格: 8
第5格: 16
……
第64格
=2 ×2 ×2
= 2 ×2 ×2 ×2
63个2
=2×2×······×2
5
5
2
2
2
5的平方(5的二次方)
2的立方(2的三次方)
面积
体积
计算下列图形中正方形的面积和立方体的体积.
5×5
记做
52
记做
23
=23
=8
那么:类似地,
5×5×5 ×5
5×5×5 ×5×5
???
5×5×???×5
n个5
分别记做
=54
=55
???
= 5n
5
5
2
2
2
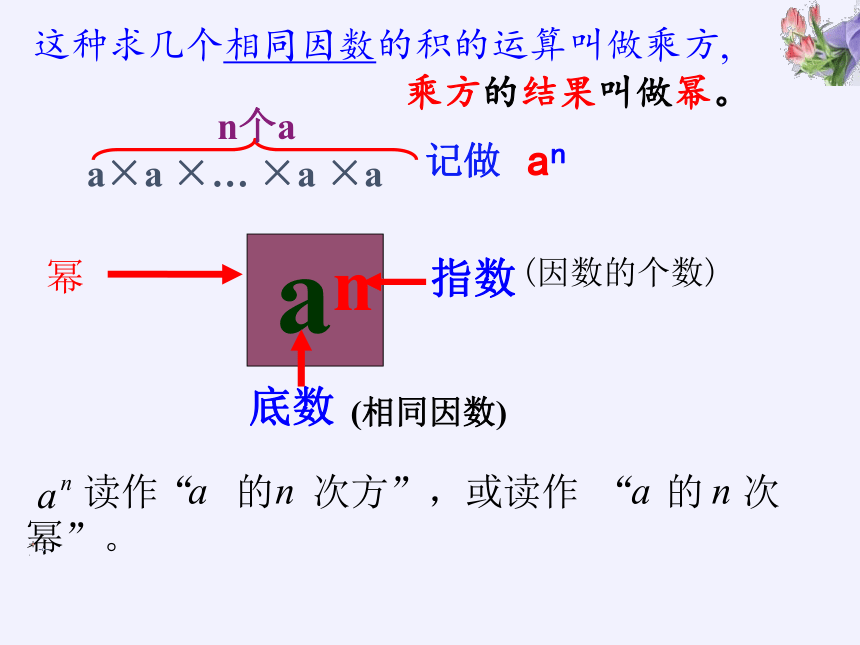
a×a ×… ×a ×a
n个a
记做
an
an
乘方的结果叫做幂。
读作“ 的 次方”,或读作 “ 的 次幂”。
幂
指数
(因数的个数)
底数
(相同因数)
这种求几个相同因数的积的运算叫做乘方,
a×a ×… ×a ×a
n个a
记做
an
轻松过关
2.(-5)2的底数是____,指数是____,(-5)2表示2个____ 相乘,叫做____的2次方,也叫做-5的_____.
-5
2
-5
-5
平方
1. ( )7表示___个 相乘,叫做 的____次方,也叫做 的___次幂,其中
叫做____ ,7叫做____;
2
9
2
9
2
9
7
7
7
底数
指数
2
9
2
9
轻松过关
3.在-52中,底数是____,指数是____, 表示_____________
2
5
5的平方的相反数
幂的底数是分数或负数时,底数应该添上括号.
4.把下列相同因数的乘积写成幂的形式.
轻松过关
(1)(-3)×(-3)
相乘的形式.
例1 计算
自主尝试
(1)(-4)3
(2)(-2)4
解
(1)(-4) 3
= (-4) × (-4) × (-4) =
(2)(-2)4
=
=
算一算,从中你发现了幂的符号有什么规律?
102 , 103 , 104 , 105
(-10)2 ,(-10)3 , (-10)4 , (-10)5
0.12 , 0.13 , 0.14 , 0.15
(-0.1)2 , (-0.1)3 , (-0.1)4 , (-0.1)5
正数的任何次方为正数,负数的偶数次方为正数,负数的奇数次方为负数.
乘方运算实际是乘法运算,根据有理数的乘法法则,可得乘方运算的法则:
非零有理数的乘方,将其绝对值乘方,而结果的符号是:正数的任何次乘方都取正号;负数的奇次方取负号、负数的偶次方乘方取正号。
0的正数次方是0.
继续探究
对于有理数的混合运算,应先乘方,再乘除,后加减;同级运算,从左到右进行;如果有括号,先做括号里的运算(按小括号、中括号、大括号的次序进行)。
例2 计算
(1) -10+8 ÷ (-2)2
有理数运算顺序
-(-4) ×(-3)
(2)
8分题
12分题
8分题
10分题
挑战自我
A. 4个5相乘 B. 5个4相乘
C. 5与4的积 D. 5个4相加的和
选一选
(2). 计算 (-1)100 + ( -1)101 的值是( )
A. 1100 B. -1 C. 0 D. -1100
B
C
(每题4分)
(1). 45 表示 ( )
填一填:
(1). 6的平方是____, -6的平方是____.
(2).比较大小(填入“>”“<”或“=”):
36
36
① 34____43 ② -0.1___ -0.13
<
>
(每空格2分)
(1) 5×23
(每题5分)
算一算:
(2) (-2)3÷22
下列运算对吗?如不对,请改正.
×
火眼金睛
( )
⑴
( )
⑵
×
8
6
(每题3分)
( )
×
(3)
( )
(-2)3= 8
-8
×
第1格: 1
第2格: 2
第3格: 4
=2×2
第4格: 8
第5格: 16
……
第64格
=2 ×2 ×2
= 2 ×2 ×2 ×2
63个2
=2×2×······×2
=22
=23
=24
=263
学以致用
棋盘上的学问
9223372036854780000
本节课你学到了什么?
1.有理数的乘方的意义和相关概念。
2.乘方的有关运算。
3.体会特殊到一般,具体到抽象的数学方法。
幂的底数是分数或负数时,底数应该添上括号.
作业
1.作业本2.5(1)
2.课后作业题2.5(1)
谢 谢
棋盘上的学问
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,就在这个棋盘上放一些米粒吧!第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
你认为国王的国库里有这么多米吗?
第64格
第1格: 1
第2格: 2
第3格: 4
=2×2
第4格: 8
第5格: 16
……
第64格
=2 ×2 ×2
= 2 ×2 ×2 ×2
63个2
=2×2×······×2
5
5
2
2
2
5的平方(5的二次方)
2的立方(2的三次方)
面积
体积
计算下列图形中正方形的面积和立方体的体积.
5×5
记做
52
记做
23
=23
=8
那么:类似地,
5×5×5 ×5
5×5×5 ×5×5
???
5×5×???×5
n个5
分别记做
=54
=55
???
= 5n
5
5
2
2
2
a×a ×… ×a ×a
n个a
记做
an
an
乘方的结果叫做幂。
读作“ 的 次方”,或读作 “ 的 次幂”。
幂
指数
(因数的个数)
底数
(相同因数)
这种求几个相同因数的积的运算叫做乘方,
a×a ×… ×a ×a
n个a
记做
an
轻松过关
2.(-5)2的底数是____,指数是____,(-5)2表示2个____ 相乘,叫做____的2次方,也叫做-5的_____.
-5
2
-5
-5
平方
1. ( )7表示___个 相乘,叫做 的____次方,也叫做 的___次幂,其中
叫做____ ,7叫做____;
2
9
2
9
2
9
7
7
7
底数
指数
2
9
2
9
轻松过关
3.在-52中,底数是____,指数是____, 表示_____________
2
5
5的平方的相反数
幂的底数是分数或负数时,底数应该添上括号.
4.把下列相同因数的乘积写成幂的形式.
轻松过关
(1)(-3)×(-3)
相乘的形式.
例1 计算
自主尝试
(1)(-4)3
(2)(-2)4
解
(1)(-4) 3
= (-4) × (-4) × (-4) =
(2)(-2)4
=
=
算一算,从中你发现了幂的符号有什么规律?
102 , 103 , 104 , 105
(-10)2 ,(-10)3 , (-10)4 , (-10)5
0.12 , 0.13 , 0.14 , 0.15
(-0.1)2 , (-0.1)3 , (-0.1)4 , (-0.1)5
正数的任何次方为正数,负数的偶数次方为正数,负数的奇数次方为负数.
乘方运算实际是乘法运算,根据有理数的乘法法则,可得乘方运算的法则:
非零有理数的乘方,将其绝对值乘方,而结果的符号是:正数的任何次乘方都取正号;负数的奇次方取负号、负数的偶次方乘方取正号。
0的正数次方是0.
继续探究
对于有理数的混合运算,应先乘方,再乘除,后加减;同级运算,从左到右进行;如果有括号,先做括号里的运算(按小括号、中括号、大括号的次序进行)。
例2 计算
(1) -10+8 ÷ (-2)2
有理数运算顺序
-(-4) ×(-3)
(2)
8分题
12分题
8分题
10分题
挑战自我
A. 4个5相乘 B. 5个4相乘
C. 5与4的积 D. 5个4相加的和
选一选
(2). 计算 (-1)100 + ( -1)101 的值是( )
A. 1100 B. -1 C. 0 D. -1100
B
C
(每题4分)
(1). 45 表示 ( )
填一填:
(1). 6的平方是____, -6的平方是____.
(2).比较大小(填入“>”“<”或“=”):
36
36
① 34____43 ② -0.1___ -0.13
<
>
(每空格2分)
(1) 5×23
(每题5分)
算一算:
(2) (-2)3÷22
下列运算对吗?如不对,请改正.
×
火眼金睛
( )
⑴
( )
⑵
×
8
6
(每题3分)
( )
×
(3)
( )
(-2)3= 8
-8
×
第1格: 1
第2格: 2
第3格: 4
=2×2
第4格: 8
第5格: 16
……
第64格
=2 ×2 ×2
= 2 ×2 ×2 ×2
63个2
=2×2×······×2
=22
=23
=24
=263
学以致用
棋盘上的学问
9223372036854780000
本节课你学到了什么?
1.有理数的乘方的意义和相关概念。
2.乘方的有关运算。
3.体会特殊到一般,具体到抽象的数学方法。
幂的底数是分数或负数时,底数应该添上括号.
作业
1.作业本2.5(1)
2.课后作业题2.5(1)
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
