沪科版七年级上册 数学 课件: 3.1一元一次方程及其解法(13张)
文档属性
| 名称 | 沪科版七年级上册 数学 课件: 3.1一元一次方程及其解法(13张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 133.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览





文档简介
一元一次方程及其解法
学 习目 标
1.熟悉利用等式的基本性质解一元一次方程的基本过程;
2.通过具体的例子归纳得出移项法则;
3.会用移项法则解方程,从中体会到利用移项法则解方程的优越性.
回顾旧知
说明下列变形是根据等式
哪一条基本性质得到的:
等式性质1
等式性质2
等式性质3
等式性质4
解方程:5x-2=8
解:两边都加上2,得
5x=8+2
__________
_______
解方程:
3x=2x+1
解:两边同时减去2x,得
_______________
___________
5x-2+2=8+2 (等式基本性质1)
5x=10
两边都除以5,得x=2 (等式基本性质2)
3x-2x=2x+1-2x (等式基本性质1)
3x-2x=1
合并同类项,得x=1
能力再现
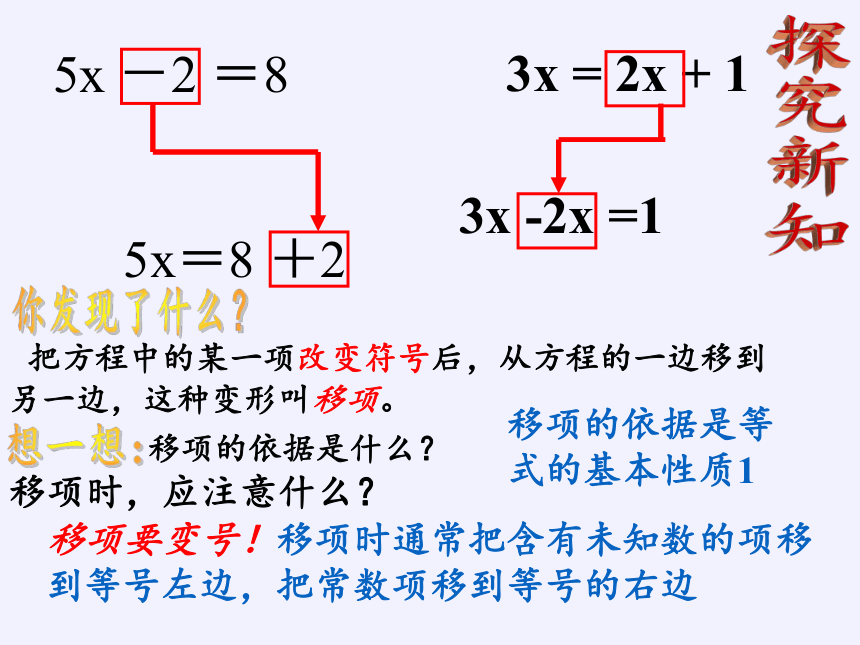
你发现了什么?
3x = 2x + 1
3x -2x =1
把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫移项。
想一想:
移项的依据是什么?
移项的依据是等式的基本性质1
移项要变号!移项时通常把含有未知数的项移到等号左边,把常数项移到等号的右边
5x -2 =8
5x=8 +2
移项时,应注意什么?
探究新知
发现问题、解决问题
1.下面的变形对不对?如果不对,应当怎样
改正?
( )
( )
( )
( )
x
x
x
x
2.下列移项正确的是( )
A由3+x=8, 得到x=8+3
B由6x=8+x,得到6x+x= -8
C由4x=3x+1,得到4x-3x=1
D由3x+2=0,得到3x=2
C
七(6)班数学老师布置了一道数学题目:
两位同学的解答正确吗?若不正确,请改正。
巩固练习
解方程:
解方程:
4x+3=-5
2x=x-6
解:
移项,得
4x=-5-3
合并同类项,得
4x=-8
两边都除以4,得
X=-2
解:
移项,得
2x-x=-6
合并同类项,得
X=-6
小试身手(当堂检测)
5-3x=2-4x
5x+3-x=2x-5
解:移项,得
4x-3x=2-5
合并同类项,得
X=-3
解:移项,得
5x-x-2x=-5-3
合并同类项,得
2x=-8
两边都除以2,得
X=-4
课堂小结
1.一般地,把方程中的某些项改变符号后,从方程的一边移到另一边, 这种变形叫做移项.
2.移项的依据是等式的基本性质1.
3.解一元一次方程需要移项时我们常把含未知数的项移到方程左边,常数项移到方程右边.
4.移项要变号.
谢 谢
学 习目 标
1.熟悉利用等式的基本性质解一元一次方程的基本过程;
2.通过具体的例子归纳得出移项法则;
3.会用移项法则解方程,从中体会到利用移项法则解方程的优越性.
回顾旧知
说明下列变形是根据等式
哪一条基本性质得到的:
等式性质1
等式性质2
等式性质3
等式性质4
解方程:5x-2=8
解:两边都加上2,得
5x=8+2
__________
_______
解方程:
3x=2x+1
解:两边同时减去2x,得
_______________
___________
5x-2+2=8+2 (等式基本性质1)
5x=10
两边都除以5,得x=2 (等式基本性质2)
3x-2x=2x+1-2x (等式基本性质1)
3x-2x=1
合并同类项,得x=1
能力再现
你发现了什么?
3x = 2x + 1
3x -2x =1
把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫移项。
想一想:
移项的依据是什么?
移项的依据是等式的基本性质1
移项要变号!移项时通常把含有未知数的项移到等号左边,把常数项移到等号的右边
5x -2 =8
5x=8 +2
移项时,应注意什么?
探究新知
发现问题、解决问题
1.下面的变形对不对?如果不对,应当怎样
改正?
( )
( )
( )
( )
x
x
x
x
2.下列移项正确的是( )
A由3+x=8, 得到x=8+3
B由6x=8+x,得到6x+x= -8
C由4x=3x+1,得到4x-3x=1
D由3x+2=0,得到3x=2
C
七(6)班数学老师布置了一道数学题目:
两位同学的解答正确吗?若不正确,请改正。
巩固练习
解方程:
解方程:
4x+3=-5
2x=x-6
解:
移项,得
4x=-5-3
合并同类项,得
4x=-8
两边都除以4,得
X=-2
解:
移项,得
2x-x=-6
合并同类项,得
X=-6
小试身手(当堂检测)
5-3x=2-4x
5x+3-x=2x-5
解:移项,得
4x-3x=2-5
合并同类项,得
X=-3
解:移项,得
5x-x-2x=-5-3
合并同类项,得
2x=-8
两边都除以2,得
X=-4
课堂小结
1.一般地,把方程中的某些项改变符号后,从方程的一边移到另一边, 这种变形叫做移项.
2.移项的依据是等式的基本性质1.
3.解一元一次方程需要移项时我们常把含未知数的项移到方程左边,常数项移到方程右边.
4.移项要变号.
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
