沪科版八年级上册 数学 课件: 13.2命题的证明(21张)
文档属性
| 名称 | 沪科版八年级上册 数学 课件: 13.2命题的证明(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 385.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览


文档简介
命题的证明
国旗上的数学
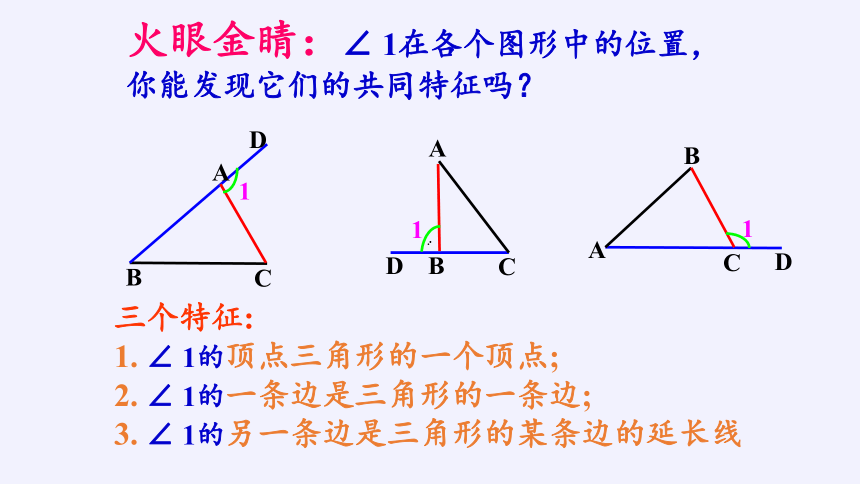
火眼金睛:∠ 1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
A
C
B
1
D
A
C
B
1
D
三个特征:
1. ∠ 1的顶点三角形的一个顶点;
2. ∠ 1的一条边是三角形的一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线
·
·
·
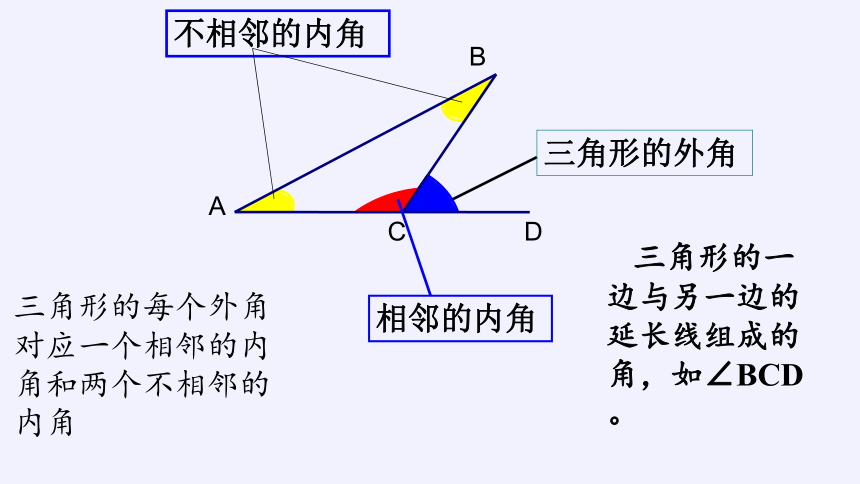
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
三角形的一边与另一边的延长线组成的角,如∠BCD。
三角形的每个外角对应一个相邻的内角和两个不相邻的内角
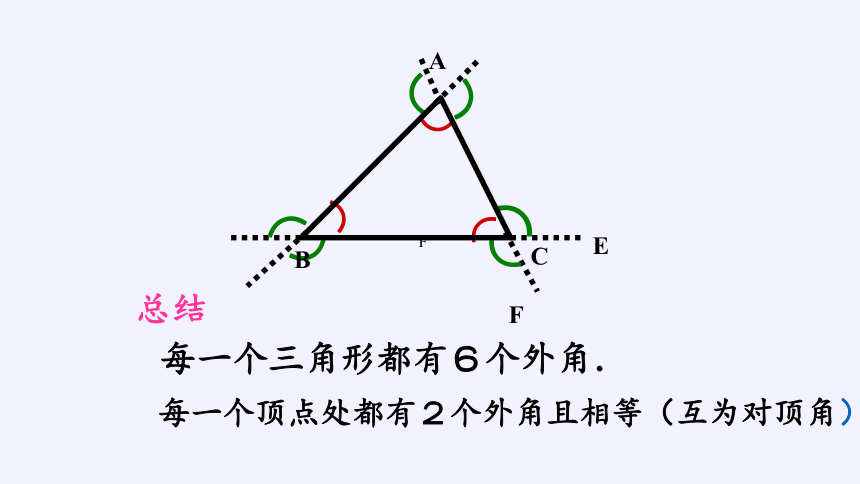
画图并思考
画△ABC,尝试画出它所有的外角。请你动手试一试并想一想△ABC的外角共有几个?
A
B
C
)
)
)
)
)
)
)
)
)
A
B
C
E
每一个三角形都有6个外角.
每一个顶点处都有2个外角且相等(互为对顶角)
总结
F
F
A
B
C
D
E
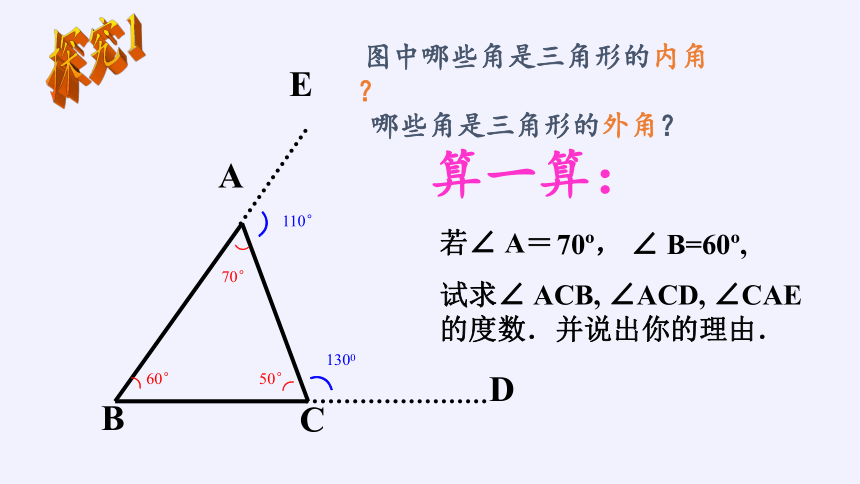
算一算:
若∠ A=
70?, ∠ B=60?,
试求∠ ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
探究1
图中哪些角是三角形的内角?
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
1300
60°
50°
70°
110°
D
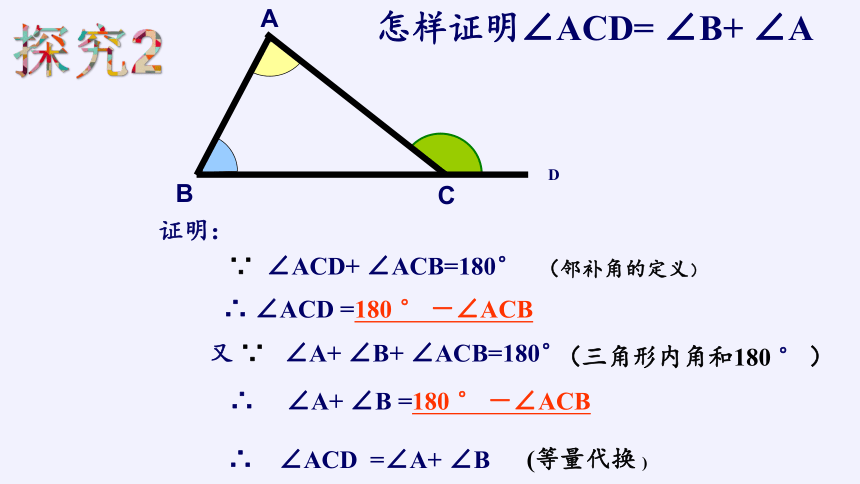
∵ ∠ACD+ ∠ACB=180°
又 ∵ ∠A+ ∠B+ ∠ACB=180°
∴ ∠ACD =∠A+ ∠B
证明:
A
B
C
∴ ∠ACD =180 ° -∠ACB
∴ ∠A+ ∠B =180 ° -∠ACB
(邻补角的定义)
(三角形内角和180 ° )
(等量代换 )
探究2
怎样证明∠ACD= ∠B+ ∠A
1
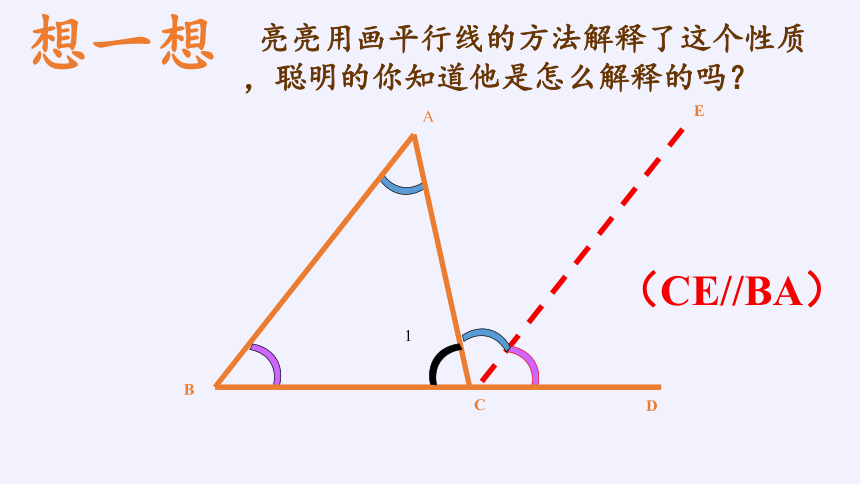
(CE//BA)
A
E
想一想
亮亮用画平行线的方法解释了这个性质,聪明的你知道他是怎么解释的吗?
C
B
D
D
解:过C作CE平行于AB
A
B
C
2
1
∴ ∠2= ∠B
(两直线平行同位角相等)
∠1= ∠A
(两直线平行内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
95?
70?
55?
30?
求下列各图中∠α的度数。
α
120?
39?
∠α=( )
α
45?
50?
∠α=( )
α
135?
80?
∠α=( )
α
45?
20?
35?
∠α=( )
α
25?
45?
∠α=( )
大显身手
81?
A
C
B
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
D
>
>
三角形的外角大于与它不相邻的任何一个内角.
探究3
把图中∠1、 ∠2、∠3按从大到小的顺序排列,并说明理由。
解:∠1> ∠2> ∠3
3
2
1
A
B
C
D
E
A
B
C
1
2
3
∠2=∠BAC+∠ACB
∠3=∠BAC+∠ABC
三个式子相加得到
∠1+ ∠2+ ∠3 = 2 ( ∠BAC+ ∠ABC+∠ACB)
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1 =∠ABC+∠ACB
解:
法1.借助外角性质说明三角形的外角和
三角形外角和等于3600
探究4
解:过A作AD∥BC
∴ ∠3= ∠4
(两直线平行,同位角相等)
B
C
1
2
3
4
A
∠2= ∠BAD
(两直线平行,同位角相等)
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°
D
借助平行线说明“三角形的外角和等于360°”
基本思想:转化
法2
如图,计算∠BOC
学以致用
C
B
O
A
F
C
B
O
A
F
∠BOC=∠BOF + ∠COF
=∠OBA + ∠1+∠OCA + ∠2
=∠OBA+∠OCA +∠1 +∠2
∠1+ ∠2=∠BAC
1
2
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角
∴∠1=∠B+ ∠E
同理∠2=∠A+∠D
在△CFG中
∠C+∠1+∠2=180?
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180?
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
学以致用
这节课你收获了什么?
小结:
1知识:外角的定义和性质
2数学思想方法:转化(化归)思想
谢 谢
国旗上的数学
火眼金睛:∠ 1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
A
C
B
1
D
A
C
B
1
D
三个特征:
1. ∠ 1的顶点三角形的一个顶点;
2. ∠ 1的一条边是三角形的一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线
·
·
·
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
三角形的一边与另一边的延长线组成的角,如∠BCD。
三角形的每个外角对应一个相邻的内角和两个不相邻的内角
画图并思考
画△ABC,尝试画出它所有的外角。请你动手试一试并想一想△ABC的外角共有几个?
A
B
C
)
)
)
)
)
)
)
)
)
A
B
C
E
每一个三角形都有6个外角.
每一个顶点处都有2个外角且相等(互为对顶角)
总结
F
F
A
B
C
D
E
算一算:
若∠ A=
70?, ∠ B=60?,
试求∠ ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
探究1
图中哪些角是三角形的内角?
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
1300
60°
50°
70°
110°
D
∵ ∠ACD+ ∠ACB=180°
又 ∵ ∠A+ ∠B+ ∠ACB=180°
∴ ∠ACD =∠A+ ∠B
证明:
A
B
C
∴ ∠ACD =180 ° -∠ACB
∴ ∠A+ ∠B =180 ° -∠ACB
(邻补角的定义)
(三角形内角和180 ° )
(等量代换 )
探究2
怎样证明∠ACD= ∠B+ ∠A
1
(CE//BA)
A
E
想一想
亮亮用画平行线的方法解释了这个性质,聪明的你知道他是怎么解释的吗?
C
B
D
D
解:过C作CE平行于AB
A
B
C
2
1
∴ ∠2= ∠B
(两直线平行同位角相等)
∠1= ∠A
(两直线平行内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
95?
70?
55?
30?
求下列各图中∠α的度数。
α
120?
39?
∠α=( )
α
45?
50?
∠α=( )
α
135?
80?
∠α=( )
α
45?
20?
35?
∠α=( )
α
25?
45?
∠α=( )
大显身手
81?
A
C
B
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
D
>
>
三角形的外角大于与它不相邻的任何一个内角.
探究3
把图中∠1、 ∠2、∠3按从大到小的顺序排列,并说明理由。
解:∠1> ∠2> ∠3
3
2
1
A
B
C
D
E
A
B
C
1
2
3
∠2=∠BAC+∠ACB
∠3=∠BAC+∠ABC
三个式子相加得到
∠1+ ∠2+ ∠3 = 2 ( ∠BAC+ ∠ABC+∠ACB)
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1 =∠ABC+∠ACB
解:
法1.借助外角性质说明三角形的外角和
三角形外角和等于3600
探究4
解:过A作AD∥BC
∴ ∠3= ∠4
(两直线平行,同位角相等)
B
C
1
2
3
4
A
∠2= ∠BAD
(两直线平行,同位角相等)
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°
D
借助平行线说明“三角形的外角和等于360°”
基本思想:转化
法2
如图,计算∠BOC
学以致用
C
B
O
A
F
C
B
O
A
F
∠BOC=∠BOF + ∠COF
=∠OBA + ∠1+∠OCA + ∠2
=∠OBA+∠OCA +∠1 +∠2
∠1+ ∠2=∠BAC
1
2
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角
∴∠1=∠B+ ∠E
同理∠2=∠A+∠D
在△CFG中
∠C+∠1+∠2=180?
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180?
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
学以致用
这节课你收获了什么?
小结:
1知识:外角的定义和性质
2数学思想方法:转化(化归)思想
谢 谢
