沪科版八年级上册 数学 课件: 15.2 线段的垂直平分线(12张)
文档属性
| 名称 | 沪科版八年级上册 数学 课件: 15.2 线段的垂直平分线(12张) |  | |
| 格式 | pptx | ||
| 文件大小 | 759.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 09:29:09 | ||
图片预览




文档简介
15.2 线段的垂直平分线
1.学习全等三角形时,主要研究了哪些内容?
温故类比
2.如何研究线段的垂直平分线呢?
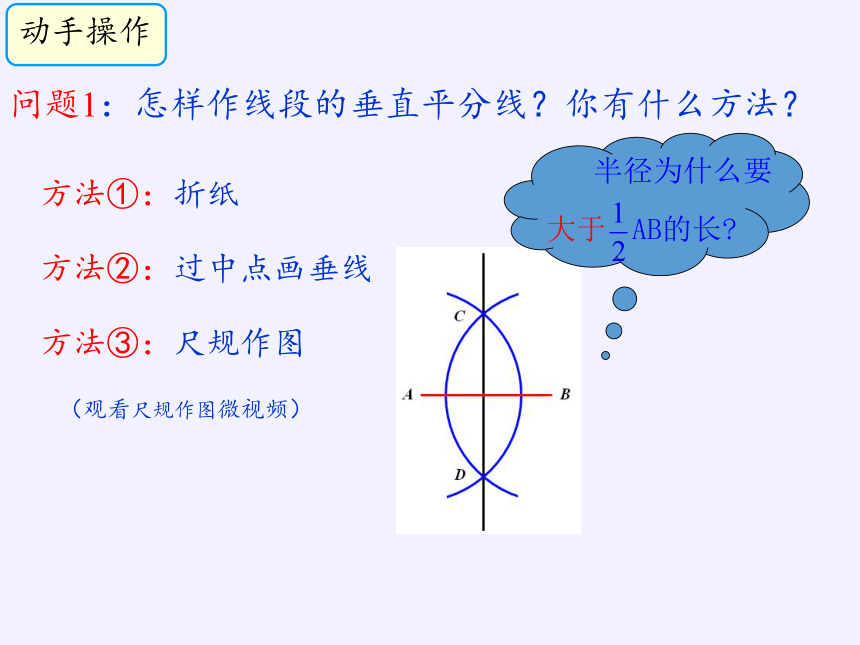
问题1:怎样作线段的垂直平分线?你有什么方法?
方法②:过中点画垂线
动手操作
方法①:折纸
方法③:尺规作图
(观看尺规作图微视频)
问题探究
O
问题2:直线CD是线段AB的垂直平分线吗?理由是什么?
先利用SSS证△ACD≌△BCD,
可得∠ACO= ∠BCO,
再利用SAS证△ACO≌ △BCO,
所以AO=BO, ∠ AOC= ∠BOC,
由平角定义得∠ AOC= ∠BOC=90°, 所以CD⊥AB.
根据垂直平分线定义可知:直线CD是线段AB的垂直平分线.
思路分析:
问题探究
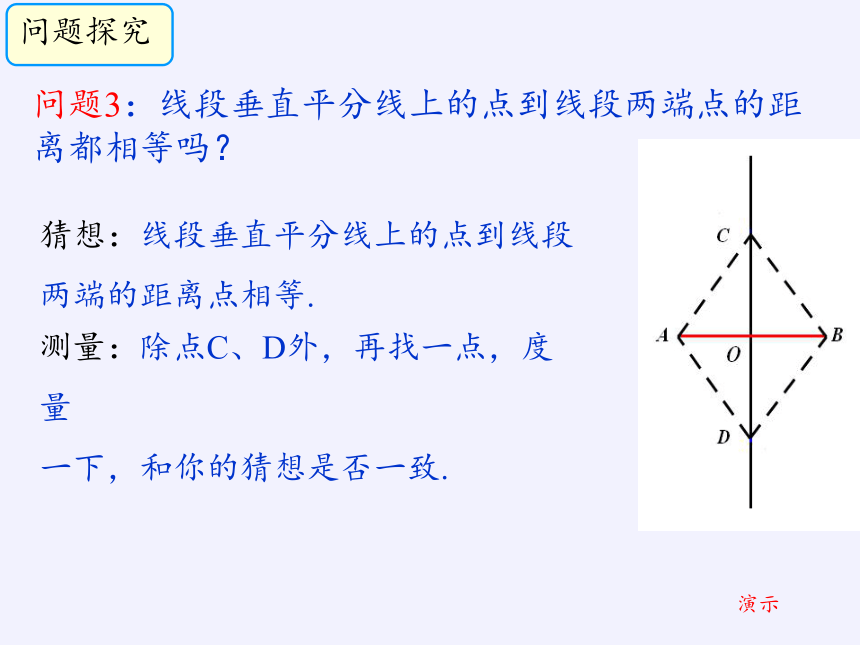
测量:除点C、D外,再找一点,度量
一下,和你的猜想是否一致.
问题3:线段垂直平分线上的点到线段两端点的距离都相等吗?
演示
猜想:线段垂直平分线上的点到线段
两端的距离点相等.
已知:如图,直线MN经过线段AB的中点O,且MN ⊥AB,P是MN上任意一点.
M
N
P
A
O
B
证明:∵MN ⊥AB , (已知)
∴∠AOP=∠BOP=90°. (垂直定义)
∵ AO=BO,(已知)
PO=PO,(公共边)
∴ △AOP≌△BOP(SAS),
∴PA=PB(全等三角形对应边相等).
命题:线段垂直平分线上的点到线段两端点的距离相等.
求证:PA=PB.
问题探究
性质定理:线段垂直平分线上的点到线段两端点距离相等.
该性质是证明两条线段相等的方法之一.
几何语言(如图):∵MN⊥ AB,AO=BO,P是MN上的任意一点.
∴PA= PB.
M
N
P
A
O
B
获得结论
1.若点P在线段AB的垂直平分线上,PA+ PB =6,则PB= .
解:∵DE是AB的垂直平分线,
∴EB=EA,
2.如图,DE是△ABC边AB的垂直平分线,交AB、BC于D、E,若AC+BC=5,求△AEC的周长.
变式:其他条件不变,对调一个条件与所求的结论,即若△AEC的周长为5,你如何求AC+BC的长.
∴△AEC的周长
=AC+CE+EA
=AC+CE+EB
=AC+BC
=5.
B
A
D
E
C
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
谈谈收获
作业
1.必做题:P 130 第2题
2.思考题: 垂直平分线性质定理的逆命题是什么,并判断该命题的真假。
3.选做题:P 131 第3题
谢 谢
1.学习全等三角形时,主要研究了哪些内容?
温故类比
2.如何研究线段的垂直平分线呢?
问题1:怎样作线段的垂直平分线?你有什么方法?
方法②:过中点画垂线
动手操作
方法①:折纸
方法③:尺规作图
(观看尺规作图微视频)
问题探究
O
问题2:直线CD是线段AB的垂直平分线吗?理由是什么?
先利用SSS证△ACD≌△BCD,
可得∠ACO= ∠BCO,
再利用SAS证△ACO≌ △BCO,
所以AO=BO, ∠ AOC= ∠BOC,
由平角定义得∠ AOC= ∠BOC=90°, 所以CD⊥AB.
根据垂直平分线定义可知:直线CD是线段AB的垂直平分线.
思路分析:
问题探究
测量:除点C、D外,再找一点,度量
一下,和你的猜想是否一致.
问题3:线段垂直平分线上的点到线段两端点的距离都相等吗?
演示
猜想:线段垂直平分线上的点到线段
两端的距离点相等.
已知:如图,直线MN经过线段AB的中点O,且MN ⊥AB,P是MN上任意一点.
M
N
P
A
O
B
证明:∵MN ⊥AB , (已知)
∴∠AOP=∠BOP=90°. (垂直定义)
∵ AO=BO,(已知)
PO=PO,(公共边)
∴ △AOP≌△BOP(SAS),
∴PA=PB(全等三角形对应边相等).
命题:线段垂直平分线上的点到线段两端点的距离相等.
求证:PA=PB.
问题探究
性质定理:线段垂直平分线上的点到线段两端点距离相等.
该性质是证明两条线段相等的方法之一.
几何语言(如图):∵MN⊥ AB,AO=BO,P是MN上的任意一点.
∴PA= PB.
M
N
P
A
O
B
获得结论
1.若点P在线段AB的垂直平分线上,PA+ PB =6,则PB= .
解:∵DE是AB的垂直平分线,
∴EB=EA,
2.如图,DE是△ABC边AB的垂直平分线,交AB、BC于D、E,若AC+BC=5,求△AEC的周长.
变式:其他条件不变,对调一个条件与所求的结论,即若△AEC的周长为5,你如何求AC+BC的长.
∴△AEC的周长
=AC+CE+EA
=AC+CE+EB
=AC+BC
=5.
B
A
D
E
C
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
谈谈收获
作业
1.必做题:P 130 第2题
2.思考题: 垂直平分线性质定理的逆命题是什么,并判断该命题的真假。
3.选做题:P 131 第3题
谢 谢
