华东师大版七年级上册 数学 课件 :2.9.1有理数的乘法法则(19张)
文档属性
| 名称 | 华东师大版七年级上册 数学 课件 :2.9.1有理数的乘法法则(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 315.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 09:41:13 | ||
图片预览





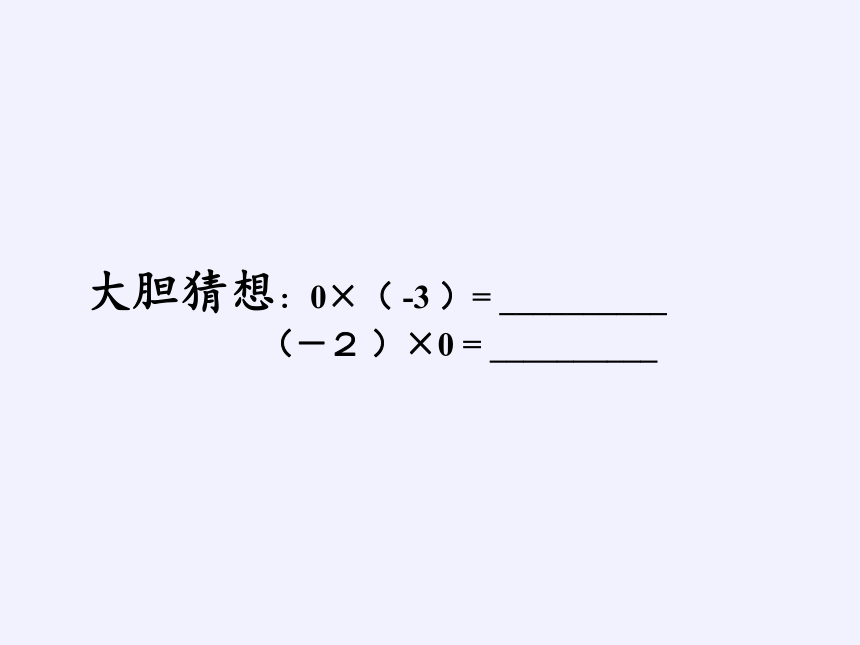
文档简介
有理数的乘法法则
教学目标
1.理解有理数乘法的意义,
2.掌握有理数的乘法法则,
3.能熟练运用有理数乘法法则进行乘法运算;
教学重点:运用有理数乘法法则进行乘法运算。
教学难点:有理数乘法运算中符号确定的理解。
活动一、创设情境, 探究新知
如果记蜗牛向右爬行为正,则向左爬行2cm应记作什么?
-2cm
活动一、创设情境, 探究新知
一只蜗牛沿直线l爬行,它现在的位置恰在l上的点O。(规定向右为正)回答下列问题:
(1)如果蜗牛一直以每分2cm的速度向右爬行,3分钟后它在什么位置?
8
10
-2
-4
-6
结果:应在O点的 处。
列式:
(+2)×(+3) =+6
右边6cm
结果:应在O点的 处。
列式:
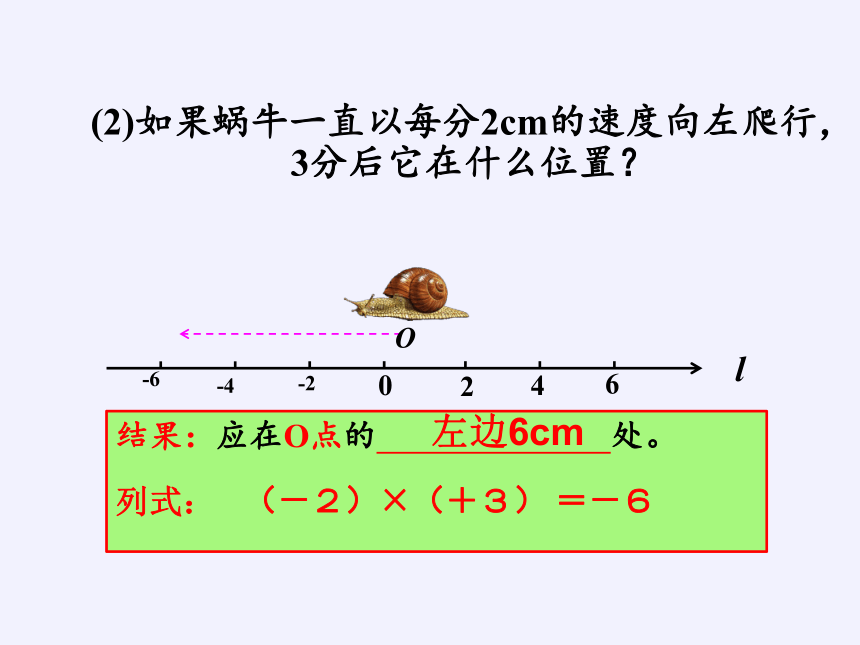
(2)如果蜗牛一直以每分2cm的速度向左爬行,3分后它在什么位置?
-2
-4
-6
(-2)×(+3) =-6
左边6cm
(+2)×(+3) = +6
(-2)×(+3) = -6
仔细观察这两个算式左边的因数有什么区别?右边的结果有什么关系呢?能得到什么结论?
试一试:
(+2 )×(-3) =
(-2 )×(-3) =
- 6
+ 6
结论:两数相乘,若把一个因数换成它的相反数,
则所得的积是原来的积的相反数.
大胆猜想:0×( -3 )= __________
(-2 )×0 = __________
(+2)×(+3) = + 6
(-2 )×(+3) = - 6
请同学们观察上述出现的四个式子,思考下列问题:
(2)积的绝对值与这两个乘数的绝对值有什么关系?
( +2 )×(-3) = - 6
(-2 )×(-3) = + 6
(1)两数相乘时,积的符号与这两个数的符号有什么关系?
问题讨论:
(1)(+2)×(+3)= + 6
(2)(-2)×(-3)= + 6
(3)(-2)×(+3)= - 6
(4)(+2)×(-3)= - 6
(5)何数同0相乘
同号
异号
绝对值相乘
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与零相乘,都得零。
都得0
有理数乘法法则:
得正
得负
活动二、深入思考 , 总结法则
被乘数
乘数
积的符号
积的绝对值
结果
-5
7
15
6
-30
-6
4
-25
1.填空题
-
35
-35
+
90
90
+
180
180
-
100
-100
活动三、应用新知, 形成技能
例1 计算:
解:
思考:有理数乘法的步骤是什么?
观察后两个能得到什么结论?
例2 计算:
解:
练习1、老师讲完有理数的乘法后,出了一道检测题,
同学们的计算结果却不相同,聪明的你,一定能帮老师找出正确结果!
学生1
学生2
学生3
活动四、巩固法则,提高技能
练习2、计算:
活动四、巩固法则,提高技能
练习3 趣味数学
在整数-5、-3、-1、0、2、6中,任取两个数相乘,所得积的最大值是多少?
活动四、巩固法则,提高技能
乘积是1的两个数互为倒数
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数与0相乘,都得0
有理数
的乘法
法则
倒数
解题步骤
定号
绝对值相乘
活动五、归纳小结
活动五、归纳小结, 回顾反思
本节课你学到了什么思想方法 ?
转化思想:有理数乘法确定符号后转化成小学乘法;带分数转化成假分数.
分类的思想
作业:
P46 第3题
谢 谢
教学目标
1.理解有理数乘法的意义,
2.掌握有理数的乘法法则,
3.能熟练运用有理数乘法法则进行乘法运算;
教学重点:运用有理数乘法法则进行乘法运算。
教学难点:有理数乘法运算中符号确定的理解。
活动一、创设情境, 探究新知
如果记蜗牛向右爬行为正,则向左爬行2cm应记作什么?
-2cm
活动一、创设情境, 探究新知
一只蜗牛沿直线l爬行,它现在的位置恰在l上的点O。(规定向右为正)回答下列问题:
(1)如果蜗牛一直以每分2cm的速度向右爬行,3分钟后它在什么位置?
8
10
-2
-4
-6
结果:应在O点的 处。
列式:
(+2)×(+3) =+6
右边6cm
结果:应在O点的 处。
列式:
(2)如果蜗牛一直以每分2cm的速度向左爬行,3分后它在什么位置?
-2
-4
-6
(-2)×(+3) =-6
左边6cm
(+2)×(+3) = +6
(-2)×(+3) = -6
仔细观察这两个算式左边的因数有什么区别?右边的结果有什么关系呢?能得到什么结论?
试一试:
(+2 )×(-3) =
(-2 )×(-3) =
- 6
+ 6
结论:两数相乘,若把一个因数换成它的相反数,
则所得的积是原来的积的相反数.
大胆猜想:0×( -3 )= __________
(-2 )×0 = __________
(+2)×(+3) = + 6
(-2 )×(+3) = - 6
请同学们观察上述出现的四个式子,思考下列问题:
(2)积的绝对值与这两个乘数的绝对值有什么关系?
( +2 )×(-3) = - 6
(-2 )×(-3) = + 6
(1)两数相乘时,积的符号与这两个数的符号有什么关系?
问题讨论:
(1)(+2)×(+3)= + 6
(2)(-2)×(-3)= + 6
(3)(-2)×(+3)= - 6
(4)(+2)×(-3)= - 6
(5)何数同0相乘
同号
异号
绝对值相乘
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与零相乘,都得零。
都得0
有理数乘法法则:
得正
得负
活动二、深入思考 , 总结法则
被乘数
乘数
积的符号
积的绝对值
结果
-5
7
15
6
-30
-6
4
-25
1.填空题
-
35
-35
+
90
90
+
180
180
-
100
-100
活动三、应用新知, 形成技能
例1 计算:
解:
思考:有理数乘法的步骤是什么?
观察后两个能得到什么结论?
例2 计算:
解:
练习1、老师讲完有理数的乘法后,出了一道检测题,
同学们的计算结果却不相同,聪明的你,一定能帮老师找出正确结果!
学生1
学生2
学生3
活动四、巩固法则,提高技能
练习2、计算:
活动四、巩固法则,提高技能
练习3 趣味数学
在整数-5、-3、-1、0、2、6中,任取两个数相乘,所得积的最大值是多少?
活动四、巩固法则,提高技能
乘积是1的两个数互为倒数
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数与0相乘,都得0
有理数
的乘法
法则
倒数
解题步骤
定号
绝对值相乘
活动五、归纳小结
活动五、归纳小结, 回顾反思
本节课你学到了什么思想方法 ?
转化思想:有理数乘法确定符号后转化成小学乘法;带分数转化成假分数.
分类的思想
作业:
P46 第3题
谢 谢
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
