华东师大版七年级上册 数学 课件: 2.9.2有理数乘法的运算律(25张)
文档属性
| 名称 | 华东师大版七年级上册 数学 课件: 2.9.2有理数乘法的运算律(25张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 456.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览





文档简介
有理数乘法的运算律
问题一、有理数包括哪些数?
有理数包括正整数、正分数、负整数、负分数和零.
问题二、计算
(1)3×2; (2) 3× ; (3) × ; (4) ×0; (5)0×0.
答案:6; ; ; 0; 0.
一、知识回顾
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
二、提出问题
问题:怎样计算?
(1)(-4)×(-5)
(2) (-5)×(+6)
如图,一只蜗牛沿直线 l爬行,它
现在的位置在l上的点O.
l
O
三、新课探究
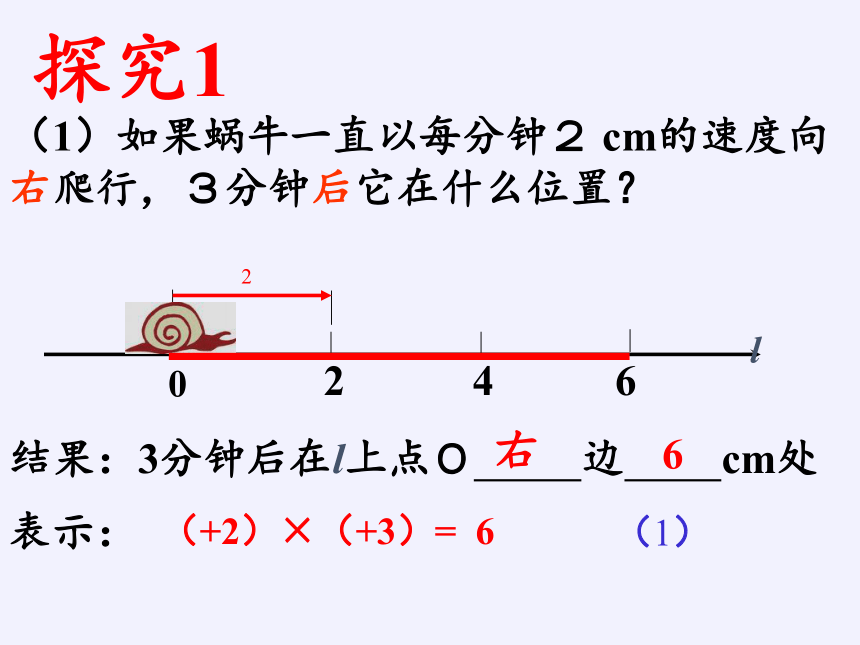
(1)如果蜗牛一直以每分2cm的速度向右爬行,3分后它在什么位置?
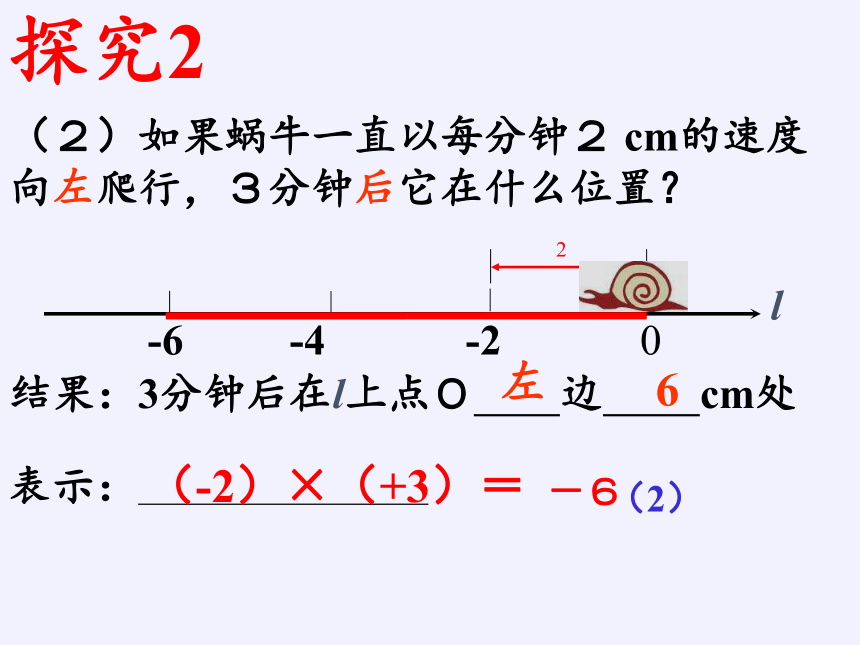
(2)如果蜗牛一直以每分2cm的速度向左爬行,3分后它在什么位置?
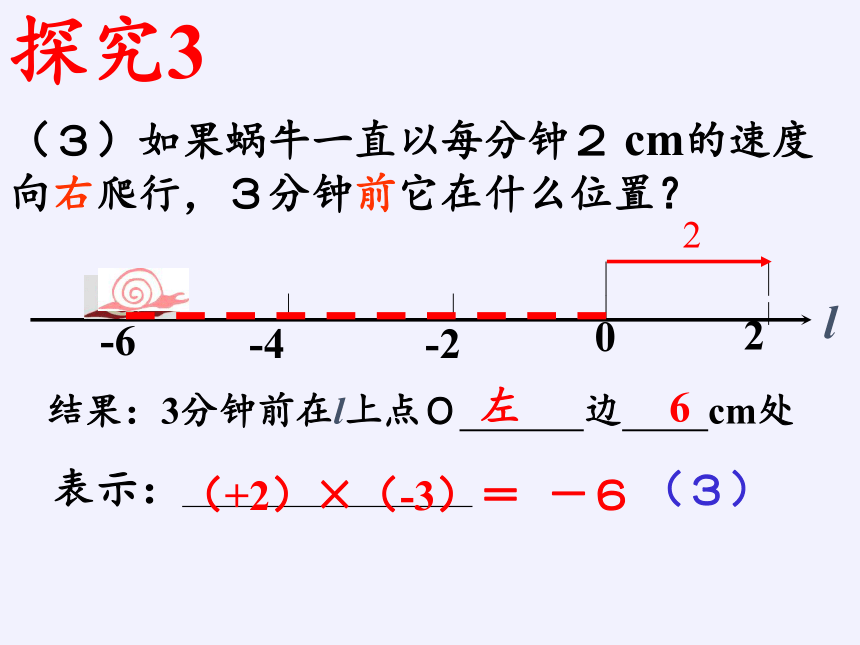
(3)如果蜗牛一直以每分2cm的速度向右爬行,3分前它在什么位置?
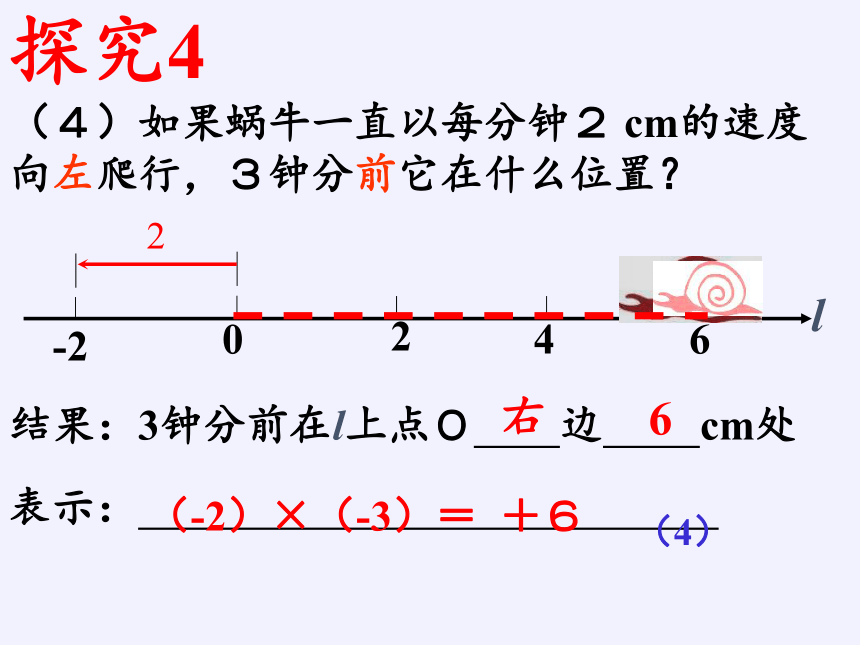
(4)如果蜗牛一直以每分2cm的速度向左爬行,3分前它在什么位置?
规定:向左为负,向右为正.
现在前为负,现在后为正.
为了区分方向与时间:
探究1
2
0
2
6
4
l
结果:3分钟后在l上点O 边 cm处
表示:
右
6
(+2)×(+3)= 6
(1)
(1)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟后它在什么位置?
(2)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟后它在什么位置?
探究2
-6
-4
0
-2
2
l
结果:3分钟后在l上点O 边 cm处
左
6
表示:
(-2)×(+3)=
(2)
-6
(3)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟前它在什么位置?
探究3
2
-6
-4
0
-2
2
l
结果:3分钟前在l上点O 边 cm处
表示:
(+2)×(-3)=
-6
左
6
(3)
(4)如果蜗牛一直以每分钟2 cm的速度向左爬行,3钟分前它在什么位置?
探究4
2
0
2
6
4
-2
l
结果:3钟分前在l上点O 边 cm处
右
6
表示:
(-2)×(-3)=
(4)
+6
答:结果都是仍在原处,即结果都是 ,若用式子表达:
探究5
(5)原地不动或运动了零次,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
零
O
四、观察与思考
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
两个数相乘,一个因数变成了它的相反数,
积也就变成了它的相反数
四、观察与思考
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
根据你对有理数乘法的思考,总结填空:
正数乘正数积为__数:负数乘负数积为__数:
负数乘正数积为__数:正数乘负数积为__数:
乘积的绝对值等于各乘数绝对值的_____。
正
正
负
负
积
(同号得正)
(异号得负)
零与任何数相乘或任何数与零相乘结果是 。
零
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。
讨论:
(1)若a<0, b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
先阅读,再填空:
(-5)×(-3)………….同号两数相乘
(-5)×(-3)=+( )…………得正
5 × 3= 15………………把绝对值相乘
所以 (-5) ×(-3)= 15
填空:(-7)× 4……____________________
(-7)× 4 = -( )………___________
7× 4 = 28………_____________
所以 (-7)× 4 = ____________
异号两数相乘
得负
把绝对值相乘
-28
例1 计算:
(1) 9×6 ; (2) (?9)×6 ;
解:(1) 9×6 (2) (?9)×6
= +(9×6) = ?(9×6)
=54 ; = ? 54;
(3) 3 × (-4)(4)(-3) × (-4)
= 12;
有理数乘法的求解步骤:
先确定积的符号
再确定积的绝对值
(3) 3 ×(-4) (4)(-3)×(-4)
= ?(3 ×4) = +(3×4)
= ? 12;
三、典型例题
被乘数
乘数
积的符号
积的绝对值
结果
-5
7
15
6
-30
-6
4
-25
1.填空题
2、确定乘积符号,并计算结果:
(1)7×(-9); (2)4×5;
(3)(-7)×(-9) (4)(-12)×3.
(5) (6)-2009×0
-
35
-35
+
90
90
+
180
180
-
100
-100
例2 计算:
(1) ×2 ; (2) (- ) × ( -2 ) 。
解:(1) ×2 = 1
(2)(- )×(-2)=1
观察上面两题有何特点?
总结:有理数中仍然有:乘积是1的两个数互为倒数.
?数a(a≠0)的倒数是什么?
(a≠0时,a的倒数是 )
说出下列各数的倒数:
1,-1, ,- ,5,-5,0.75,-
1,
-1,
3,
—3,
例3 用正负数表示气温的变化量,上升为正,下降为负。登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃。
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:规定:提价为正,降价为负
(-5)×60=-300
答:销售额减少300元.
归纳总结
1、有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。
3、乘积是1的两个数互为倒数。
2、有理数的求解步骤:有理数相乘,先确定积的符号,再确定积的绝对值。
2、已知|x|=2,|y|=3,且xy<0,则x-y= .
拓展探究
1、已知a、b互为相反数,c、d互为倒数,e是绝
对值最小的数,计算:(a+b)+ — (a+b)e
布置作业:P38
1、(1),(3),(5);
2、(1),(2),(3),(4);
3、(2),(3),(4),(5)。
数学就在身边
愿你有更多的发现……
凭勤奋出成果
向效率要质量
拼搏 进取 勤奋 认 真
再 见
谢 谢
问题一、有理数包括哪些数?
有理数包括正整数、正分数、负整数、负分数和零.
问题二、计算
(1)3×2; (2) 3× ; (3) × ; (4) ×0; (5)0×0.
答案:6; ; ; 0; 0.
一、知识回顾
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
二、提出问题
问题:怎样计算?
(1)(-4)×(-5)
(2) (-5)×(+6)
如图,一只蜗牛沿直线 l爬行,它
现在的位置在l上的点O.
l
O
三、新课探究
(1)如果蜗牛一直以每分2cm的速度向右爬行,3分后它在什么位置?
(2)如果蜗牛一直以每分2cm的速度向左爬行,3分后它在什么位置?
(3)如果蜗牛一直以每分2cm的速度向右爬行,3分前它在什么位置?
(4)如果蜗牛一直以每分2cm的速度向左爬行,3分前它在什么位置?
规定:向左为负,向右为正.
现在前为负,现在后为正.
为了区分方向与时间:
探究1
2
0
2
6
4
l
结果:3分钟后在l上点O 边 cm处
表示:
右
6
(+2)×(+3)= 6
(1)
(1)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟后它在什么位置?
(2)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟后它在什么位置?
探究2
-6
-4
0
-2
2
l
结果:3分钟后在l上点O 边 cm处
左
6
表示:
(-2)×(+3)=
(2)
-6
(3)如果蜗牛一直以每分钟2 cm的速度向右爬行,3分钟前它在什么位置?
探究3
2
-6
-4
0
-2
2
l
结果:3分钟前在l上点O 边 cm处
表示:
(+2)×(-3)=
-6
左
6
(3)
(4)如果蜗牛一直以每分钟2 cm的速度向左爬行,3钟分前它在什么位置?
探究4
2
0
2
6
4
-2
l
结果:3钟分前在l上点O 边 cm处
右
6
表示:
(-2)×(-3)=
(4)
+6
答:结果都是仍在原处,即结果都是 ,若用式子表达:
探究5
(5)原地不动或运动了零次,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
零
O
四、观察与思考
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
两个数相乘,一个因数变成了它的相反数,
积也就变成了它的相反数
四、观察与思考
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
根据你对有理数乘法的思考,总结填空:
正数乘正数积为__数:负数乘负数积为__数:
负数乘正数积为__数:正数乘负数积为__数:
乘积的绝对值等于各乘数绝对值的_____。
正
正
负
负
积
(同号得正)
(异号得负)
零与任何数相乘或任何数与零相乘结果是 。
零
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。
讨论:
(1)若a<0, b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
先阅读,再填空:
(-5)×(-3)………….同号两数相乘
(-5)×(-3)=+( )…………得正
5 × 3= 15………………把绝对值相乘
所以 (-5) ×(-3)= 15
填空:(-7)× 4……____________________
(-7)× 4 = -( )………___________
7× 4 = 28………_____________
所以 (-7)× 4 = ____________
异号两数相乘
得负
把绝对值相乘
-28
例1 计算:
(1) 9×6 ; (2) (?9)×6 ;
解:(1) 9×6 (2) (?9)×6
= +(9×6) = ?(9×6)
=54 ; = ? 54;
(3) 3 × (-4)(4)(-3) × (-4)
= 12;
有理数乘法的求解步骤:
先确定积的符号
再确定积的绝对值
(3) 3 ×(-4) (4)(-3)×(-4)
= ?(3 ×4) = +(3×4)
= ? 12;
三、典型例题
被乘数
乘数
积的符号
积的绝对值
结果
-5
7
15
6
-30
-6
4
-25
1.填空题
2、确定乘积符号,并计算结果:
(1)7×(-9); (2)4×5;
(3)(-7)×(-9) (4)(-12)×3.
(5) (6)-2009×0
-
35
-35
+
90
90
+
180
180
-
100
-100
例2 计算:
(1) ×2 ; (2) (- ) × ( -2 ) 。
解:(1) ×2 = 1
(2)(- )×(-2)=1
观察上面两题有何特点?
总结:有理数中仍然有:乘积是1的两个数互为倒数.
?数a(a≠0)的倒数是什么?
(a≠0时,a的倒数是 )
说出下列各数的倒数:
1,-1, ,- ,5,-5,0.75,-
1,
-1,
3,
—3,
例3 用正负数表示气温的变化量,上升为正,下降为负。登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃。
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:规定:提价为正,降价为负
(-5)×60=-300
答:销售额减少300元.
归纳总结
1、有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。
3、乘积是1的两个数互为倒数。
2、有理数的求解步骤:有理数相乘,先确定积的符号,再确定积的绝对值。
2、已知|x|=2,|y|=3,且xy<0,则x-y= .
拓展探究
1、已知a、b互为相反数,c、d互为倒数,e是绝
对值最小的数,计算:(a+b)+ — (a+b)e
布置作业:P38
1、(1),(3),(5);
2、(1),(2),(3),(4);
3、(2),(3),(4),(5)。
数学就在身边
愿你有更多的发现……
凭勤奋出成果
向效率要质量
拼搏 进取 勤奋 认 真
再 见
谢 谢
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
