华东师大版八年级上册:13.3.1 等腰三角形的性质 课件 (13张ppt)
文档属性
| 名称 | 华东师大版八年级上册:13.3.1 等腰三角形的性质 课件 (13张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 256.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览




文档简介
等腰三角形的性质
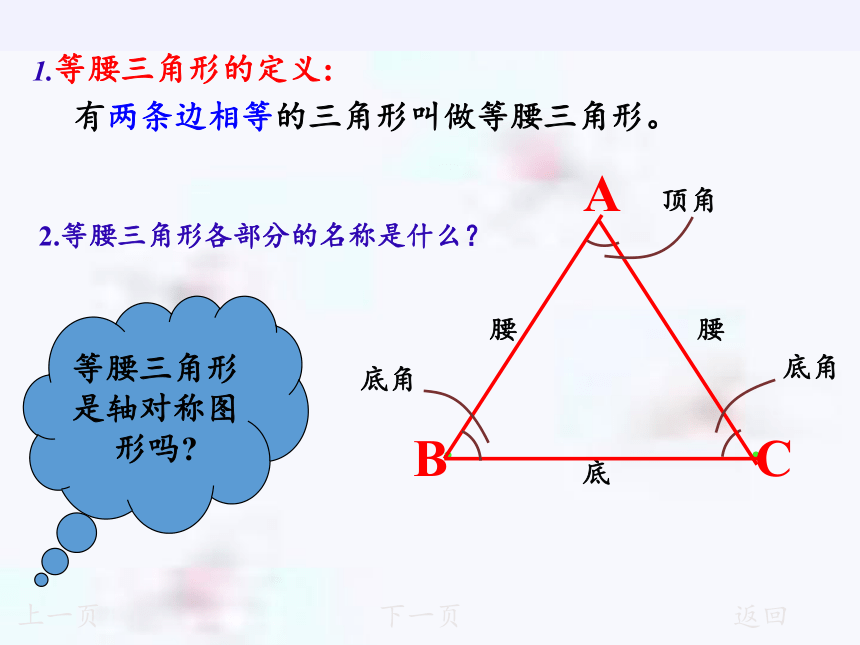
1.等腰三角形的定义:
腰
腰
底
顶角
底角
底角
2.等腰三角形各部分的名称是什么?
上一页
下一页
返回
A
B
C
有两条边相等的三角形叫做等腰三角形。
等腰三角形是轴对称图形吗?
动手操作
请同学们拿出一张纸,画一个等腰三角形,并把它剪下来。
A
B
C
D
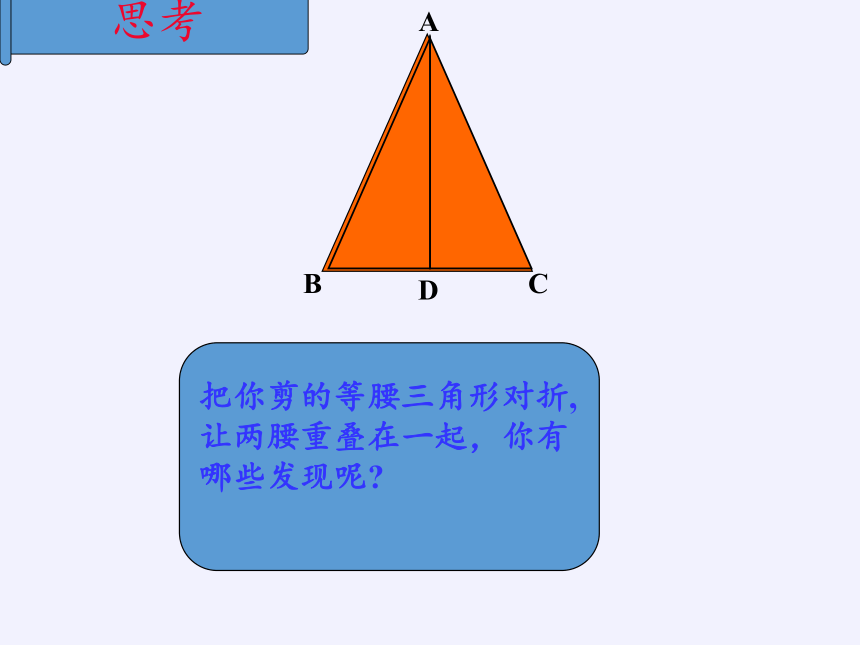
思考
把你剪的等腰三角形对折,让两腰重叠在一起,你有哪些发现呢?
性质1: 等腰三角形的两个底角相等
(简写成“ 等边对等角”)
归纳
A
B
C
D
1
2
证明:作顶角∠A的平分线AD,在 BAD和 CAD中
AB = AC (已知)
∠1 = ∠2 (辅助线作法)
AD = AD (公共边)
∴ BAD ≌ CAD (SAS)
∴ ∠B = ∠C (全等三角形的对应角相等)
{
已知: ABC中 , AB = AC (如图).
求证:∠ B = ∠ C .
求证:等腰三角形的两个底角相等。
我是最棒的
2. 已知等腰三角形的一个角等于40°,那么它的另外两个
角的度数分别是 ;
3. 已知等腰三角形的一个角等于120°, 那么它的另外两
个角的度数是 ;
4. 已知等腰三角形一角是另一角的2倍,则各内角的度数
分别是 。
1. 已知等腰三角形的一个底角等于40°,那么它的另外两个角的度数分别是 ;
40°,100°
40°,100°或70°, 70°
30°,30°
45°, 45°, 90° 或 36°,72°, 72°
0°<顶角<180°
0°<底角<90°
顶角度数+2×底角度数= 180°
小小发现
在等腰三角形中
上一页
下一页
探索
在上面的证明过程中,由 △ADB≌ △ADC
你还能得到什么结论?
∠BAD = ∠CAD (AD平分∠BAC)
BD = CD ( AD 平分BC )
∠ADB = ∠ADC = 90°( AD⊥BC )
性质2:等腰三角形的顶角平分线、底边上
的中线、底边上的高互相重合.简称
三线合一.
A
B
C
D
(1)∵AD⊥BC,
∴∠ =∠ , = ;
(2)∵AD是中线,
∴ ⊥ ,∠ =∠ ;
(3)∵AD是角平分线,
∴ ⊥ , = .
上一页
下一页
返回
A
B
C
D
填空:根据三线合一性质,在 △ ABC中,AB=AC时
BAD
CAD
BD
DC
AD
BC
BAD
CAD
AD
BC
BD
DC
10
课堂小结
1.等腰三角形是轴对称图形,等腰三角形的定义,以及相关概念。
2.等腰三角形的两底角相等。(简写成“等边对等角”)
3、等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。(简称“三线合一”)
4、注意等腰三角形的顶角和底角的取值范围:
0°<顶角<180°,0°<底角<90°
作业布置
课本P84 习题13.3 1,2,3,4题
谢 谢
1.等腰三角形的定义:
腰
腰
底
顶角
底角
底角
2.等腰三角形各部分的名称是什么?
上一页
下一页
返回
A
B
C
有两条边相等的三角形叫做等腰三角形。
等腰三角形是轴对称图形吗?
动手操作
请同学们拿出一张纸,画一个等腰三角形,并把它剪下来。
A
B
C
D
思考
把你剪的等腰三角形对折,让两腰重叠在一起,你有哪些发现呢?
性质1: 等腰三角形的两个底角相等
(简写成“ 等边对等角”)
归纳
A
B
C
D
1
2
证明:作顶角∠A的平分线AD,在 BAD和 CAD中
AB = AC (已知)
∠1 = ∠2 (辅助线作法)
AD = AD (公共边)
∴ BAD ≌ CAD (SAS)
∴ ∠B = ∠C (全等三角形的对应角相等)
{
已知: ABC中 , AB = AC (如图).
求证:∠ B = ∠ C .
求证:等腰三角形的两个底角相等。
我是最棒的
2. 已知等腰三角形的一个角等于40°,那么它的另外两个
角的度数分别是 ;
3. 已知等腰三角形的一个角等于120°, 那么它的另外两
个角的度数是 ;
4. 已知等腰三角形一角是另一角的2倍,则各内角的度数
分别是 。
1. 已知等腰三角形的一个底角等于40°,那么它的另外两个角的度数分别是 ;
40°,100°
40°,100°或70°, 70°
30°,30°
45°, 45°, 90° 或 36°,72°, 72°
0°<顶角<180°
0°<底角<90°
顶角度数+2×底角度数= 180°
小小发现
在等腰三角形中
上一页
下一页
探索
在上面的证明过程中,由 △ADB≌ △ADC
你还能得到什么结论?
∠BAD = ∠CAD (AD平分∠BAC)
BD = CD ( AD 平分BC )
∠ADB = ∠ADC = 90°( AD⊥BC )
性质2:等腰三角形的顶角平分线、底边上
的中线、底边上的高互相重合.简称
三线合一.
A
B
C
D
(1)∵AD⊥BC,
∴∠ =∠ , = ;
(2)∵AD是中线,
∴ ⊥ ,∠ =∠ ;
(3)∵AD是角平分线,
∴ ⊥ , = .
上一页
下一页
返回
A
B
C
D
填空:根据三线合一性质,在 △ ABC中,AB=AC时
BAD
CAD
BD
DC
AD
BC
BAD
CAD
AD
BC
BD
DC
10
课堂小结
1.等腰三角形是轴对称图形,等腰三角形的定义,以及相关概念。
2.等腰三角形的两底角相等。(简写成“等边对等角”)
3、等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。(简称“三线合一”)
4、注意等腰三角形的顶角和底角的取值范围:
0°<顶角<180°,0°<底角<90°
作业布置
课本P84 习题13.3 1,2,3,4题
谢 谢
