华东师大版八年级上册 数学 课件: 13.2.6斜边直角边(23张)
文档属性
| 名称 | 华东师大版八年级上册 数学 课件: 13.2.6斜边直角边(23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 375.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 11:33:45 | ||
图片预览








文档简介
斜边直角边
如图,舞台背景的形状是两个直角三角形,每个三角形都有一条直角边被花盆遮住无法测量,工作人员想知道这两个直角三角形是否全等.
复习提问
证明两个三角形全等有哪些方法?
1、SAS(边角边)
2、ASA(角边角)
3、AAS(角角边)
4、SSS(边边边)
回忆
两边及其中一边的对角对应相等的两个三角形全等吗?
不一定全等。
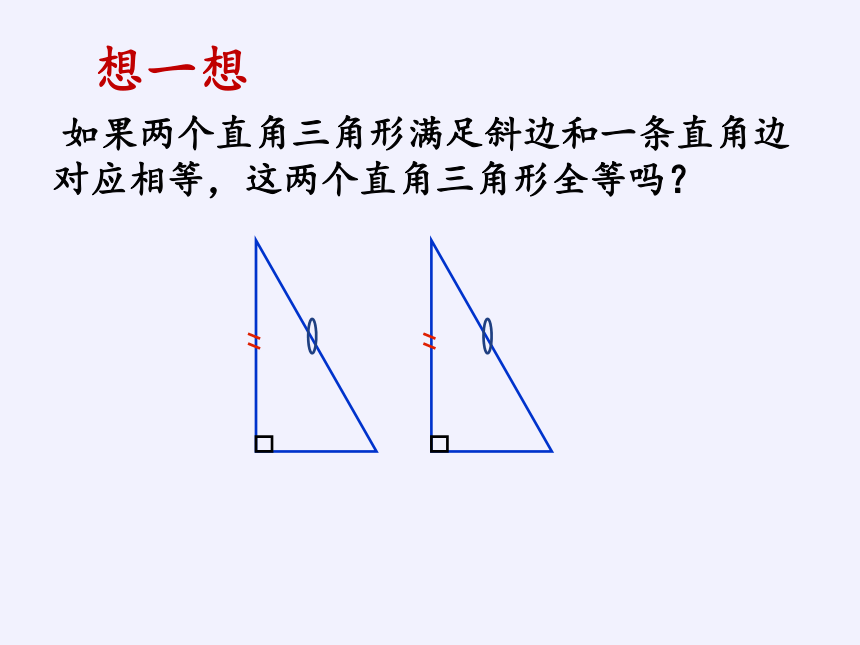
想一想
如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
做一做,说一说
请同学们拿出自己所做的卡片,并与同伴交流。
定理:斜边和一条直角边分别相等的两个直角三角形全等。简记为 HL (或斜边直角边)
A
Bˊ
Cˊ
Aˊ
B
C
几何语言:
在Rt△ABC和Rt△AˊBˊCˊ中
∵AB=AˊBˊ
AC=AˊCˊ
∴Rt△ABC≌Rt△AˊBˊCˊ(HL)
例1、如图,AC=BD,∠C ﹦∠ D ﹦90°.
求证:BC=AD
证明:∵∠C ﹦∠ D ﹦90°(已知)
∴ 与 都是直角三角形(直角三角形的定义)
在Rt△ABC和Rt△BAD中
∵AB=BA(公共边) AC=BD(已知)
∴Rt△ABC≌Rt△BAD(HL)
∴BC=AD(全等三角形的对应边相等)
1.已知:如图,在△ABC中, D为BC的中点.DE⊥AB,DF⊥AC,点E、F为垂足,DE=DF
D
B
C
A
E
F
小试牛刀
求证:△BED≌ △CFD
┐
┐
2.如图,AC=AD,∠C﹦∠D﹦90°,
求证:BC=BD.
A
C
B
D
┐
┐
一题多变:
若把划线处条件替换为∠ABC=∠ABD 如何证明呢?
能力提升
已知:如图,AD为△ABC的高,E为
AC上一点,BE交AD于点F,且有
┐
A
F
E
D
C
B
一题多变:
若把划线处条件替换为BD=AD, FD=CD 如何证明呢?
求证:BE⊥AC
BF=AC,FD=CD
议一议
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
∠ABC+∠DFE=90°.
探究应用
解:在Rt△ABC和Rt△DEF中
∵ BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (H.L.)
∴∠ABC=∠DEF(全等三角形对 应角相等).
∵ ∠DEF+∠DFE=90°(直角三角形两个锐 角互余)
∴∠ABC+∠DFE=90°(等量代换)
直角三角形全等的判定
一般三角形全等的判定
S.A.S
A.S.A
A.A.S
S.S.S
S.A.S
A.S.A
A.A.S
H.L
灵活运用各种方法证明直角三角形全等
归纳归纳
S.S.S
小结
请你谈谈这节课的收获。
作业:
1.课本76页第6题
2.导练101页基础反思
比一比,看谁反应快
1、如图,AC⊥BC,AC⊥AD,垂足分别是C,A,AB=DC,由此可判定两个全等的三角形是 和
┐
┐
A
C
D
B
2、如图,在 中,∠C=90 ?,AC=AE,
DE⊥AB,且∠CDA=55? ,则∠BDE=
E
┐
┐
C
A
B
D
谢谢
拓展创新
如图,在△ABC中,∠C ﹦90°,AC=10,BC=5.线段PQ=AB,P,Q两点
分别在AC和过点A且垂直于AC的射线AX上运动,当AP= 时,才能使△ABC与△QPA全等。
┐
A
X
C
B
Q
P
(P)
Q
谢 谢
如图,舞台背景的形状是两个直角三角形,每个三角形都有一条直角边被花盆遮住无法测量,工作人员想知道这两个直角三角形是否全等.
复习提问
证明两个三角形全等有哪些方法?
1、SAS(边角边)
2、ASA(角边角)
3、AAS(角角边)
4、SSS(边边边)
回忆
两边及其中一边的对角对应相等的两个三角形全等吗?
不一定全等。
想一想
如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
做一做,说一说
请同学们拿出自己所做的卡片,并与同伴交流。
定理:斜边和一条直角边分别相等的两个直角三角形全等。简记为 HL (或斜边直角边)
A
Bˊ
Cˊ
Aˊ
B
C
几何语言:
在Rt△ABC和Rt△AˊBˊCˊ中
∵AB=AˊBˊ
AC=AˊCˊ
∴Rt△ABC≌Rt△AˊBˊCˊ(HL)
例1、如图,AC=BD,∠C ﹦∠ D ﹦90°.
求证:BC=AD
证明:∵∠C ﹦∠ D ﹦90°(已知)
∴ 与 都是直角三角形(直角三角形的定义)
在Rt△ABC和Rt△BAD中
∵AB=BA(公共边) AC=BD(已知)
∴Rt△ABC≌Rt△BAD(HL)
∴BC=AD(全等三角形的对应边相等)
1.已知:如图,在△ABC中, D为BC的中点.DE⊥AB,DF⊥AC,点E、F为垂足,DE=DF
D
B
C
A
E
F
小试牛刀
求证:△BED≌ △CFD
┐
┐
2.如图,AC=AD,∠C﹦∠D﹦90°,
求证:BC=BD.
A
C
B
D
┐
┐
一题多变:
若把划线处条件替换为∠ABC=∠ABD 如何证明呢?
能力提升
已知:如图,AD为△ABC的高,E为
AC上一点,BE交AD于点F,且有
┐
A
F
E
D
C
B
一题多变:
若把划线处条件替换为BD=AD, FD=CD 如何证明呢?
求证:BE⊥AC
BF=AC,FD=CD
议一议
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
∠ABC+∠DFE=90°.
探究应用
解:在Rt△ABC和Rt△DEF中
∵ BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (H.L.)
∴∠ABC=∠DEF(全等三角形对 应角相等).
∵ ∠DEF+∠DFE=90°(直角三角形两个锐 角互余)
∴∠ABC+∠DFE=90°(等量代换)
直角三角形全等的判定
一般三角形全等的判定
S.A.S
A.S.A
A.A.S
S.S.S
S.A.S
A.S.A
A.A.S
H.L
灵活运用各种方法证明直角三角形全等
归纳归纳
S.S.S
小结
请你谈谈这节课的收获。
作业:
1.课本76页第6题
2.导练101页基础反思
比一比,看谁反应快
1、如图,AC⊥BC,AC⊥AD,垂足分别是C,A,AB=DC,由此可判定两个全等的三角形是 和
┐
┐
A
C
D
B
2、如图,在 中,∠C=90 ?,AC=AE,
DE⊥AB,且∠CDA=55? ,则∠BDE=
E
┐
┐
C
A
B
D
谢谢
拓展创新
如图,在△ABC中,∠C ﹦90°,AC=10,BC=5.线段PQ=AB,P,Q两点
分别在AC和过点A且垂直于AC的射线AX上运动,当AP= 时,才能使△ABC与△QPA全等。
┐
A
X
C
B
Q
P
(P)
Q
谢 谢
