华东师大版九年级上册 数学 课件: 24.4解直角三角形(12张)
文档属性
| 名称 | 华东师大版九年级上册 数学 课件: 24.4解直角三角形(12张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 194.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 10:13:37 | ||
图片预览





文档简介
解直角三角形
如图,Rt△ABC共有六个元素(三条边,三个角),其中
∠C=90°,那么其余五个元素(三边a,b,c,两锐角A,B)之
间有怎样的关系呢?
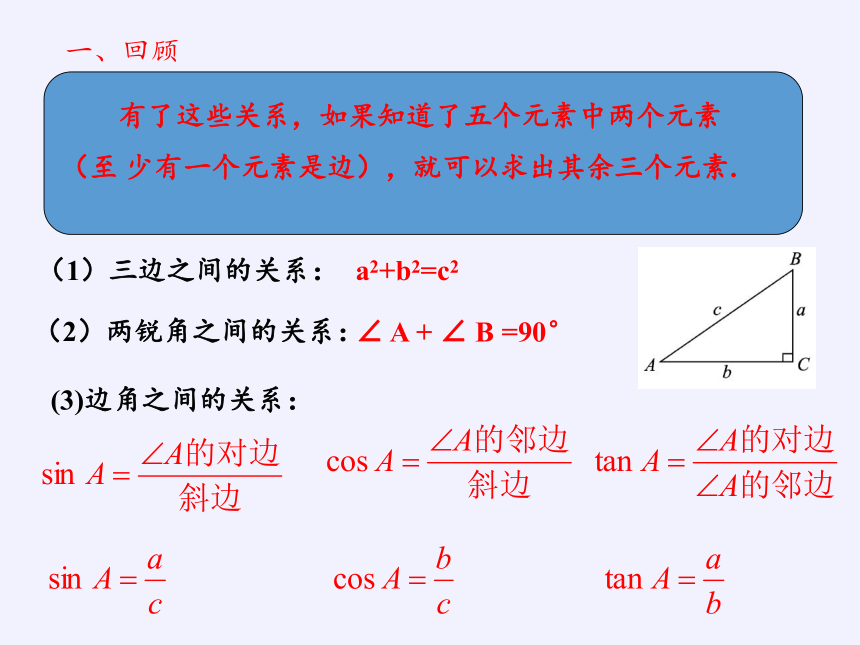
(1)三边之间的关系:
a2+b2=c2
(2)两锐角之间的关系:
∠ A + ∠ B =90°
(3)边角之间的关系:
一、回顾
有了这些关系,如果知道了五个元素中两个元素
(至 少有一个元素是边),就可以求出其余三个元素.
解直角三角形:
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
题型一:已知一边一锐角,求未知的边角;
题型二:已知两边,求未知的边角.
方法:
合理选择边与边、角与角以及边角之间的关系,
常常是:有角先求角,无角先求边,有边有角,要
根据“有斜选弦,无斜选切,避除就乘,宁原勿中.
二、探究:
第1课时 直角三角形的边角关系
6
10
8
练习:
第1课时 直角三角形的边角关系
3.如图△ABC中,∠C=90°,∠B=60°,
BC=6,解此三角形.
4.已知:如图,Rt△ABC中,∠C=90°,c=5,∠A=36°,解这个直角三角形.
第1课时 直角三角形的边角关系
[解析] 已知一边、一锐角,可先根据两锐角互余求出另一锐角,利用正弦、余弦或正切求出其余两边长.尽量利用原始数据,避免误差积累.
4.已知:如图,Rt△ABC中,∠C=90°,c=5,∠A=36°,解这个直角三角形.
第1课时 直角三角形的边角关系
[归纳总结] 已知斜边和一锐角,选择正弦、余弦求两直角边,利用两锐角互余求另一锐角.
三、知识引用:
1.如图所示,一棵大树在一次强烈的地震中离地面5米处折断倒下,树顶落在树根12米处,大树在折断之前多高?
5m
12m
2.如图,东西两炮台A,B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它南偏东40°方向,炮台B测得敌舰C在它正南方向,试求敌舰与两炮台的距离(精确到1米).
40°
2000m
A
B
C
?
3.如图所示,某市对A,B两小区的供水路线进行改造,供水站M在小区A的南偏东60°方向,在小区B的西南方向,A,B两小区之间的距离为 米,求供水站M到A,B小区的距离各是多少?
60°
A
B
M
C
a2+b2=c2
∠ A + ∠ B =90°
课 堂 小 结
(3)边角之间的关系:
(1)三边之间的关系:
(2)两锐角之间的关系:
涉斜(涉及斜边)选弦(选正弦或余弦)、无“斜”(斜边)选“切”(选正切或余切)、避除(避开除法)就乘(用乘法)、能正(能用正弦或正切)不余(不用余弦).
题型一:已知一边一锐角,求未知的边角;
题型二:已知两边,求未知的边角.
谢 谢
如图,Rt△ABC共有六个元素(三条边,三个角),其中
∠C=90°,那么其余五个元素(三边a,b,c,两锐角A,B)之
间有怎样的关系呢?
(1)三边之间的关系:
a2+b2=c2
(2)两锐角之间的关系:
∠ A + ∠ B =90°
(3)边角之间的关系:
一、回顾
有了这些关系,如果知道了五个元素中两个元素
(至 少有一个元素是边),就可以求出其余三个元素.
解直角三角形:
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
题型一:已知一边一锐角,求未知的边角;
题型二:已知两边,求未知的边角.
方法:
合理选择边与边、角与角以及边角之间的关系,
常常是:有角先求角,无角先求边,有边有角,要
根据“有斜选弦,无斜选切,避除就乘,宁原勿中.
二、探究:
第1课时 直角三角形的边角关系
6
10
8
练习:
第1课时 直角三角形的边角关系
3.如图△ABC中,∠C=90°,∠B=60°,
BC=6,解此三角形.
4.已知:如图,Rt△ABC中,∠C=90°,c=5,∠A=36°,解这个直角三角形.
第1课时 直角三角形的边角关系
[解析] 已知一边、一锐角,可先根据两锐角互余求出另一锐角,利用正弦、余弦或正切求出其余两边长.尽量利用原始数据,避免误差积累.
4.已知:如图,Rt△ABC中,∠C=90°,c=5,∠A=36°,解这个直角三角形.
第1课时 直角三角形的边角关系
[归纳总结] 已知斜边和一锐角,选择正弦、余弦求两直角边,利用两锐角互余求另一锐角.
三、知识引用:
1.如图所示,一棵大树在一次强烈的地震中离地面5米处折断倒下,树顶落在树根12米处,大树在折断之前多高?
5m
12m
2.如图,东西两炮台A,B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它南偏东40°方向,炮台B测得敌舰C在它正南方向,试求敌舰与两炮台的距离(精确到1米).
40°
2000m
A
B
C
?
3.如图所示,某市对A,B两小区的供水路线进行改造,供水站M在小区A的南偏东60°方向,在小区B的西南方向,A,B两小区之间的距离为 米,求供水站M到A,B小区的距离各是多少?
60°
A
B
M
C
a2+b2=c2
∠ A + ∠ B =90°
课 堂 小 结
(3)边角之间的关系:
(1)三边之间的关系:
(2)两锐角之间的关系:
涉斜(涉及斜边)选弦(选正弦或余弦)、无“斜”(斜边)选“切”(选正切或余切)、避除(避开除法)就乘(用乘法)、能正(能用正弦或正切)不余(不用余弦).
题型一:已知一边一锐角,求未知的边角;
题型二:已知两边,求未知的边角.
谢 谢
