苏科版八年级上册 物理 课件 5.3直线运动(22张ppt )
文档属性
| 名称 | 苏科版八年级上册 物理 课件 5.3直线运动(22张ppt ) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-22 00:00:00 | ||
图片预览





文档简介
三、直线运动
哪种运动最简单?
情景导学
情境模拟:
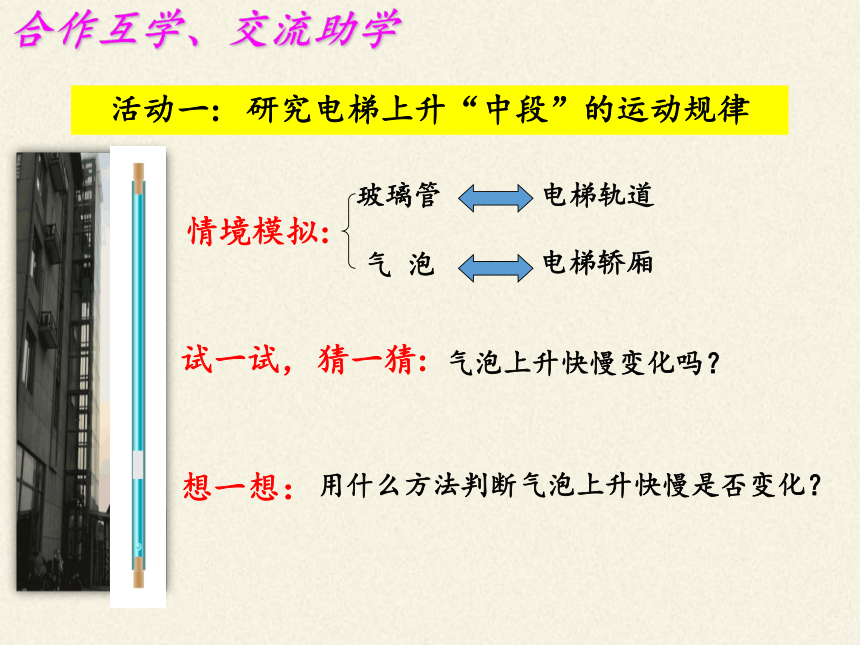
活动一: 研究电梯上升“中段”的运动规律
合作互学、交流助学
气泡上升快慢变化吗?
试一试,
玻璃管
电梯轨道
气 泡
电梯轿厢
想一想:
用什么方法判断气泡上升快慢是否变化?
猜一猜:
方案一:相同路程比时间
起点
合作互学、交流助学
方案二:相同时间比路程
S
S
S
S
t4
t1
t2
t3
t
t
t
t
S4
S1
S2
S3
起点
想一想:根据所给器材,你觉得测时间和测距离,哪种操作更方便?谈谈你的想法。
方案一:相同路程比时间
起点
合作互学、交流助学
t4
t1
t2
t3
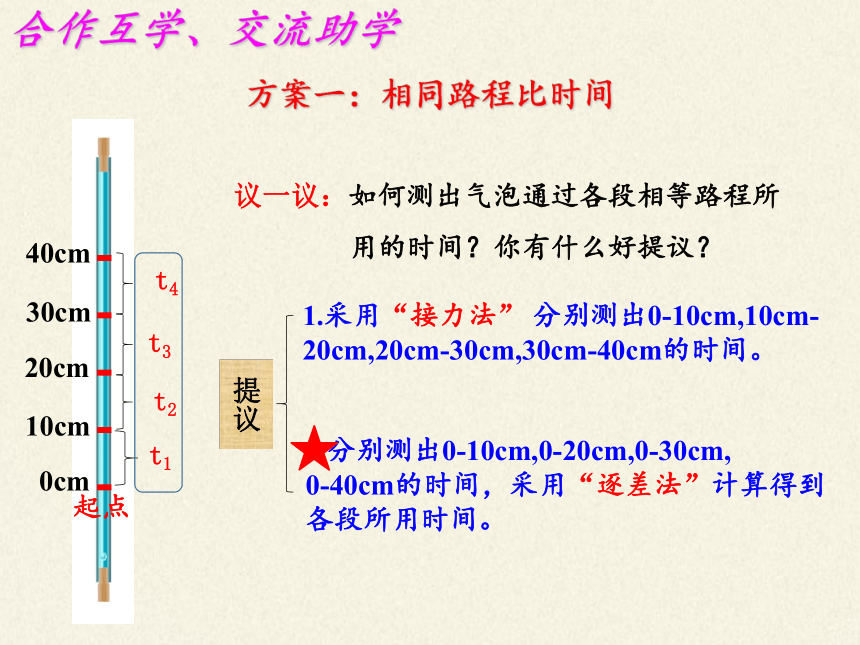
议一议:如何测出气泡通过各段相等路程所
用的时间?你有什么好提议?
0cm
30cm
20cm
10cm
40cm
1.采用“接力法” 分别测出0-10cm,10cm- 20cm,20cm-30cm,30cm-40cm的时间。
2.分别测出0-10cm,0-20cm,0-30cm,
0-40cm的时间,采用“逐差法”计算得到各段所用时间。
提议
★
合作互学、交流助学
1# 观察气泡运动并发号施令
4# 记录时间
5# 记录时间
3# 记录时间
2# 记录时间
说一说:分享小组的合作分工经验。
气泡上边缘刚好到达标记下边缘
做一做:把测得的数据分别填入对应表格中。
结论:根据数据分析发现,气泡上升中段,运动的快慢 。
合作互学、交流助学
表格二
近似不变
表格法
表格一
从O开始的路程s/cm
0
10
20
30
40
从O开始计时的时间t/s
区间s/cm
0~10
10~20
20~30
30~40
通过各区间的时间t/s
近似相等
图像法
0
40
30
20
10
S/cm
t/s
合作互学、交流助学
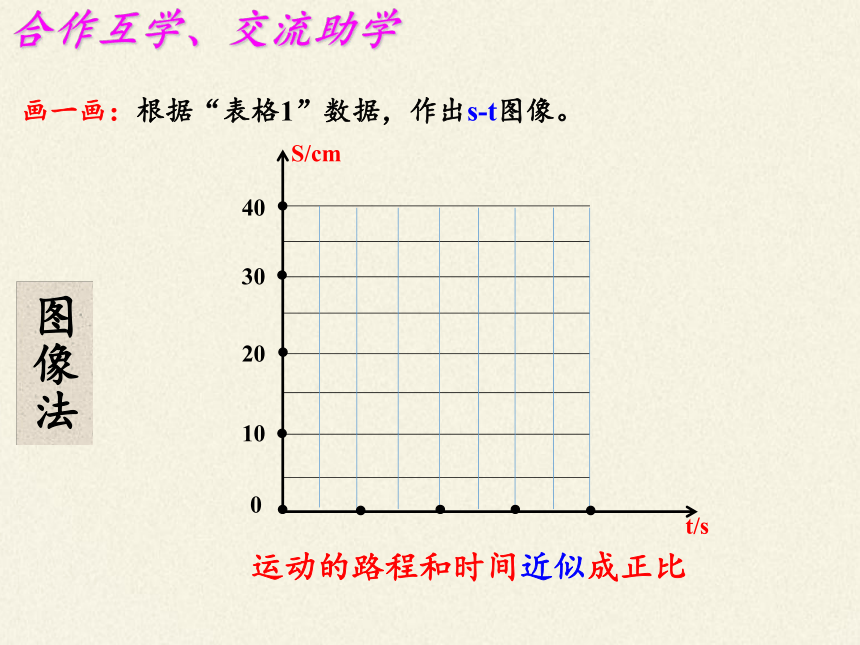
画一画:根据“表格1”数据,作出s-t图像。
运动的路程和时间近似成正比
合作互学、交流助学
图像法
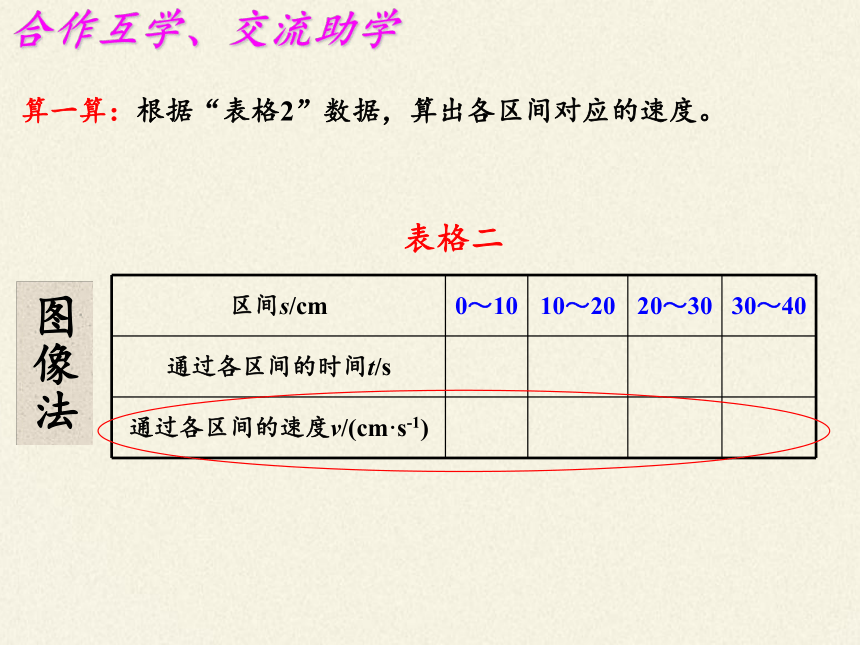
算一算:根据“表格2”数据,算出各区间对应的速度。
表格二
区间s/cm
0~10
10~20
20~30
30~40
通过各区间的时间t/s
通过各区间的速度v/(cm·s-1)
图像法
画一画:根据“表格2”数据,作出v-t大致图像。
合作互学、交流助学
1.2
0.7
0.4
0.5
v/cm·s-1
t/s
0.6
0.8
0.9
1.0
1.1
一、匀速直线运动
定义: 速度不变的直线运动叫做匀速直线运动。
合作互学、交流助学
2. 特点: 在任意相等时间内通过的路程相等。
合作互学、交流助学
下面这些运动,哪些近似匀速直线运动呢?
电梯上升中间阶段
钢索断裂,电梯坠落
自动扶梯,缓缓上行
停止蹬地后一段滑行
钢索断裂 电梯坠落
活动二: 研究“电梯坠落”的运动规律
合作互学、交流助学
猜一猜:“电梯坠落”是加速还是减速?
活动二: 研究“电梯坠落”的运动规律
合作互学、交流助学
猜一猜:“电梯坠落”是加速还是减速?
观察与发现:
1. 每相邻两位置间的时间 。(相等/不等)
2. 每相邻两位置间的距离 。(相等/不相等)
3. 苹果坠落过程中速度是 (变化/不变)的,
而且是 (加速/减速)。
相等
不相等
变化
加速
合作互学、交流助学
二、变速直线运动
定义: 我们把速度变化的直线运动叫做变速直
线运动。
合作互学、交流助学
2. 特点: 在相等时间内通过的路程不相等。
二、变速直线运动
合作互学、交流助学
3. 平均速度---- 粗略描述变速直线运动
的快慢。
4. 公式----
V平均=
S
t
5. 提醒:必须指明在哪一段时间或路程内,
求“平均速度”才有意义。
VAB=11m/s
VBC=13m/s
0.2s
0.2s
2.2m
2.6m
A
B
C
天然竖直“隧道”
2米
活动三: 学以致用
1.“轿厢完全通过隧道”、“轿
厢全部在隧道中”在计算路程时有什么不同?
2. 轿厢高2m,匀速上升,完全
通过高度为42m的“绿色天然
隧道”用时11s。求
(1)轿厢上升速度
(2)轿厢完全在隧道内运
行的时间
42
米
合作互学、交流助学
1.自学课本P114例题。
2.交流讨论--运用学到方法
解题下面的问题。
合作互学、交流助学
运动的物体具有 ,物体由于运动而具有的能,叫做 能。
能量
动
三、运动与生活
通过本节课的学习,你有哪些收获?
总结提学
达标检学
参考答案
1. B
2. A
3. 正比例 越大
4. 5 50
5. 变速直线 1
谢 谢
哪种运动最简单?
情景导学
情境模拟:
活动一: 研究电梯上升“中段”的运动规律
合作互学、交流助学
气泡上升快慢变化吗?
试一试,
玻璃管
电梯轨道
气 泡
电梯轿厢
想一想:
用什么方法判断气泡上升快慢是否变化?
猜一猜:
方案一:相同路程比时间
起点
合作互学、交流助学
方案二:相同时间比路程
S
S
S
S
t4
t1
t2
t3
t
t
t
t
S4
S1
S2
S3
起点
想一想:根据所给器材,你觉得测时间和测距离,哪种操作更方便?谈谈你的想法。
方案一:相同路程比时间
起点
合作互学、交流助学
t4
t1
t2
t3
议一议:如何测出气泡通过各段相等路程所
用的时间?你有什么好提议?
0cm
30cm
20cm
10cm
40cm
1.采用“接力法” 分别测出0-10cm,10cm- 20cm,20cm-30cm,30cm-40cm的时间。
2.分别测出0-10cm,0-20cm,0-30cm,
0-40cm的时间,采用“逐差法”计算得到各段所用时间。
提议
★
合作互学、交流助学
1# 观察气泡运动并发号施令
4# 记录时间
5# 记录时间
3# 记录时间
2# 记录时间
说一说:分享小组的合作分工经验。
气泡上边缘刚好到达标记下边缘
做一做:把测得的数据分别填入对应表格中。
结论:根据数据分析发现,气泡上升中段,运动的快慢 。
合作互学、交流助学
表格二
近似不变
表格法
表格一
从O开始的路程s/cm
0
10
20
30
40
从O开始计时的时间t/s
区间s/cm
0~10
10~20
20~30
30~40
通过各区间的时间t/s
近似相等
图像法
0
40
30
20
10
S/cm
t/s
合作互学、交流助学
画一画:根据“表格1”数据,作出s-t图像。
运动的路程和时间近似成正比
合作互学、交流助学
图像法
算一算:根据“表格2”数据,算出各区间对应的速度。
表格二
区间s/cm
0~10
10~20
20~30
30~40
通过各区间的时间t/s
通过各区间的速度v/(cm·s-1)
图像法
画一画:根据“表格2”数据,作出v-t大致图像。
合作互学、交流助学
1.2
0.7
0.4
0.5
v/cm·s-1
t/s
0.6
0.8
0.9
1.0
1.1
一、匀速直线运动
定义: 速度不变的直线运动叫做匀速直线运动。
合作互学、交流助学
2. 特点: 在任意相等时间内通过的路程相等。
合作互学、交流助学
下面这些运动,哪些近似匀速直线运动呢?
电梯上升中间阶段
钢索断裂,电梯坠落
自动扶梯,缓缓上行
停止蹬地后一段滑行
钢索断裂 电梯坠落
活动二: 研究“电梯坠落”的运动规律
合作互学、交流助学
猜一猜:“电梯坠落”是加速还是减速?
活动二: 研究“电梯坠落”的运动规律
合作互学、交流助学
猜一猜:“电梯坠落”是加速还是减速?
观察与发现:
1. 每相邻两位置间的时间 。(相等/不等)
2. 每相邻两位置间的距离 。(相等/不相等)
3. 苹果坠落过程中速度是 (变化/不变)的,
而且是 (加速/减速)。
相等
不相等
变化
加速
合作互学、交流助学
二、变速直线运动
定义: 我们把速度变化的直线运动叫做变速直
线运动。
合作互学、交流助学
2. 特点: 在相等时间内通过的路程不相等。
二、变速直线运动
合作互学、交流助学
3. 平均速度---- 粗略描述变速直线运动
的快慢。
4. 公式----
V平均=
S
t
5. 提醒:必须指明在哪一段时间或路程内,
求“平均速度”才有意义。
VAB=11m/s
VBC=13m/s
0.2s
0.2s
2.2m
2.6m
A
B
C
天然竖直“隧道”
2米
活动三: 学以致用
1.“轿厢完全通过隧道”、“轿
厢全部在隧道中”在计算路程时有什么不同?
2. 轿厢高2m,匀速上升,完全
通过高度为42m的“绿色天然
隧道”用时11s。求
(1)轿厢上升速度
(2)轿厢完全在隧道内运
行的时间
42
米
合作互学、交流助学
1.自学课本P114例题。
2.交流讨论--运用学到方法
解题下面的问题。
合作互学、交流助学
运动的物体具有 ,物体由于运动而具有的能,叫做 能。
能量
动
三、运动与生活
通过本节课的学习,你有哪些收获?
总结提学
达标检学
参考答案
1. B
2. A
3. 正比例 越大
4. 5 50
5. 变速直线 1
谢 谢
同课章节目录
