人教版数学八年级上册11.3.2 多边形的内角和 课件(共24张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.3.2 多边形的内角和 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 366.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 15:33:20 | ||
图片预览





文档简介
多边形的内角和
问题2:你知道长方形和正方形的内角和是多少吗?
其他四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度吗?
(三角形内角和 180°)
(都是360°)
导入新课
1. 从n边形的一个顶点可以引_____条对角线,
将n边形分成了________个三角形.
2. n边形的对角线一共有______ 条.
(n-3)
(n-2)
复习旧知
A
B
C
D
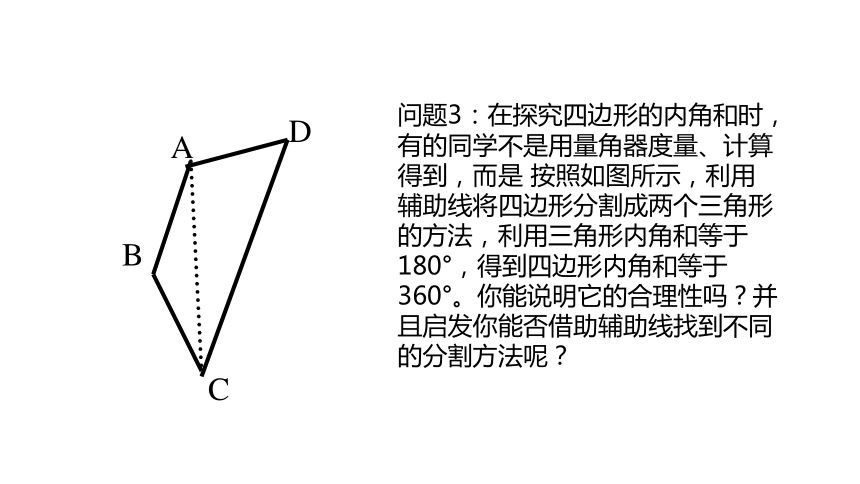
问题3:在探究四边形的内角和时,有的同学不是用量角器度量、计算得到,而是 按照如图所示,利用辅助线将四边形分割成两个三角形的方法,利用三角形内角和等于180°,得到四边形内角和等于360°。你能说明它的合理性吗?并且启发你能否借助辅助线找到不同的分割方法呢?
P
A
B
C
D
图 1
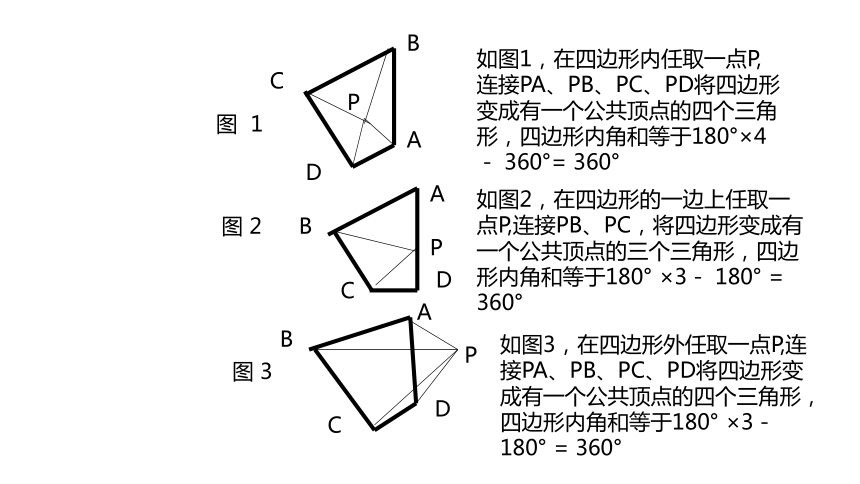
如图1,在四边形内任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180°×4 - 360°= 360°
P
A
B
D
C
图 2
如图2,在四边形的一边上任取一点P,连接PB、PC,将四边形变成有一个公共顶点的三个三角形,四边形内角和等于180° ×3- 180° = 360°
P
A
B
C
D
图 3
如图3,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180° ×3- 180° = 360°
四边形内角和为360°
B
A
C
D
E
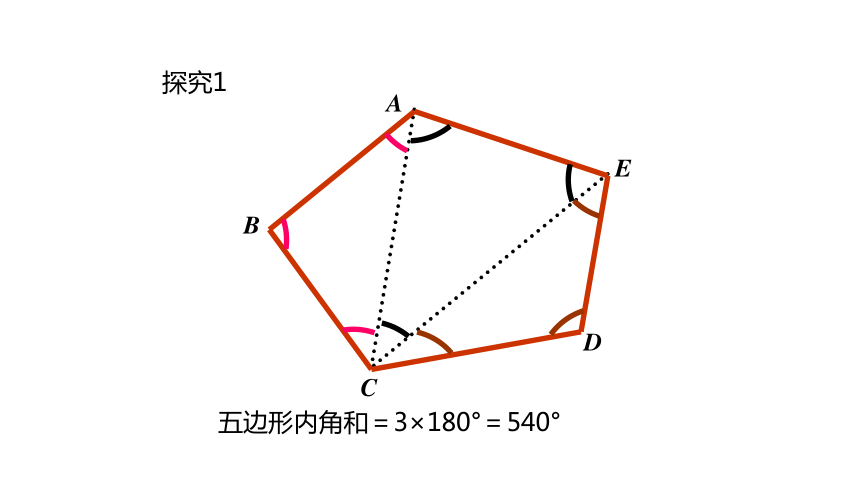
探究1
五边形内角和=3×180°=540°
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180° × 4 – 180° = 540°
E
A
B
C
D
O
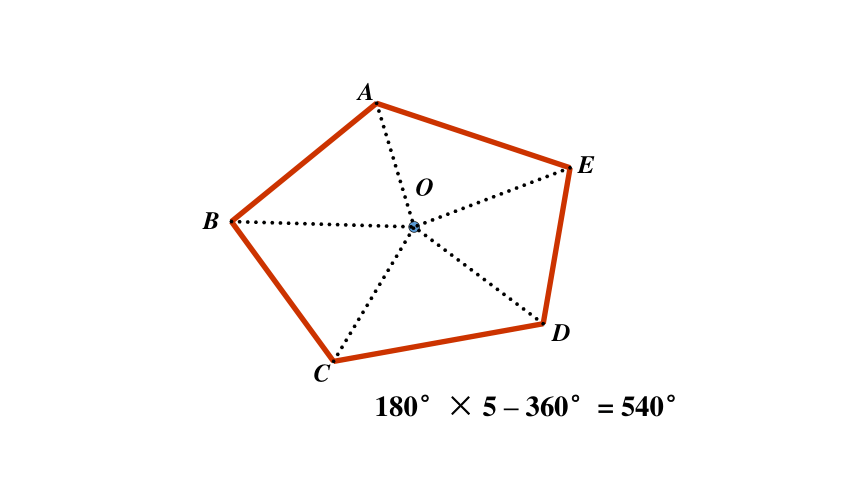
180°× 5 – 360°= 540°
A
B
C
D
E
4 × 180°-180 °
O
=540°
四边形的内角和 (4-2)× 180° = 360°
五边形的内角和 (5-2)× 180° = 540°
六边形的内角和 (6-2)× 180° =720°
七边形的内角 (7-2)× 180° = 900°
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
多边形内角和
多边形
边数
一个顶点出发的对角线条数
图形
分成三角形的个数
计算规律
三边形
四边形
五边形
六边形
n边形
…
…
…
…
…
…
3
4
5
6
n
0
n-3
1
2
3
1
2
3
4
n-2
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
n边形内角和等于(n-2)× 180°
2.如果一个多边形的内角和是1440度,那么这是 边形。
解:由多边形的内角和公式可得
(n - 2)· 180 = 1440
(n - 2) = 8
n = 10
∴这是十边形。
十
3.已知一个多边形每个内角都等于 108° ,求这个多边形的边数?
1.(抢答) 8边形的内角和等于多少度? 十边形呢?
解:设这个多边形的边数为n,根据题意得:
(n-2) ×180=108n
解得:n=5 答:这个多边形是五边形。
练习
4. 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:
如图,四边形ABCD中,
∠A+ ∠C =180°
∠A+∠B+∠C+∠D=(4-2) ×180 °
= 360 °
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360°- 180°
=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
所以
如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是__________
相等或者互补
十二边形的内角和是( ).
一个多边形当边数增加1时,它的内角和增加( ).
一个多边形的内角和是720?,则此多边形共有( )个内角.
如果一个多边形的内角和是1440°,那么这是( )边形.
1800?
180?
六
十
课堂检测
【例1】如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
思考:
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
多边形的外角和
五边形外角和
结论:五边形的外角和等于360°.
-(5-2) × 180°
=360 °
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-五边形内角和
=5×180°
【例2】如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
探究 在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
结论:n边形的外角和等于360°.
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
=n个平角-n边形内角和
= n×180 °
n边形外角和是多少度?
每个内角的度数是
每个外角的度数是
(1)若十二边形的每个内角都相等,那么每个内角是______度.
(2)已知多边形的每个内角都是135度,则这个多边形是_______.
(3)如果某个多边形的内角和等于它的外角和,那么这个多边形的边数是________.
150
八边形
四边形
练习1
练习2: 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360?,
∴ (n-2)?180°=2× 360?.
解得: n=6.
∴这个多边形的边数为6.
1、n边形的内角和等于(n-2)×180°.
??
3、利用类比归纳、转化的学习方法,可以把 多边形问题转化为三角形问题来解决; 外角问题转化为内角来解决.
4、方程的数学思想在几何中有重要的作用.
本节课你学会哪些知识?学会了哪些解决问题的方法?你还有哪些疑问?
2、n边形的外角和等于360°.
课堂小结
谢 谢 观 看!
问题2:你知道长方形和正方形的内角和是多少吗?
其他四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度吗?
(三角形内角和 180°)
(都是360°)
导入新课
1. 从n边形的一个顶点可以引_____条对角线,
将n边形分成了________个三角形.
2. n边形的对角线一共有______ 条.
(n-3)
(n-2)
复习旧知
A
B
C
D
问题3:在探究四边形的内角和时,有的同学不是用量角器度量、计算得到,而是 按照如图所示,利用辅助线将四边形分割成两个三角形的方法,利用三角形内角和等于180°,得到四边形内角和等于360°。你能说明它的合理性吗?并且启发你能否借助辅助线找到不同的分割方法呢?
P
A
B
C
D
图 1
如图1,在四边形内任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180°×4 - 360°= 360°
P
A
B
D
C
图 2
如图2,在四边形的一边上任取一点P,连接PB、PC,将四边形变成有一个公共顶点的三个三角形,四边形内角和等于180° ×3- 180° = 360°
P
A
B
C
D
图 3
如图3,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180° ×3- 180° = 360°
四边形内角和为360°
B
A
C
D
E
探究1
五边形内角和=3×180°=540°
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180° × 4 – 180° = 540°
E
A
B
C
D
O
180°× 5 – 360°= 540°
A
B
C
D
E
4 × 180°-180 °
O
=540°
四边形的内角和 (4-2)× 180° = 360°
五边形的内角和 (5-2)× 180° = 540°
六边形的内角和 (6-2)× 180° =720°
七边形的内角 (7-2)× 180° = 900°
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
多边形内角和
多边形
边数
一个顶点出发的对角线条数
图形
分成三角形的个数
计算规律
三边形
四边形
五边形
六边形
n边形
…
…
…
…
…
…
3
4
5
6
n
0
n-3
1
2
3
1
2
3
4
n-2
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
n边形内角和等于(n-2)× 180°
2.如果一个多边形的内角和是1440度,那么这是 边形。
解:由多边形的内角和公式可得
(n - 2)· 180 = 1440
(n - 2) = 8
n = 10
∴这是十边形。
十
3.已知一个多边形每个内角都等于 108° ,求这个多边形的边数?
1.(抢答) 8边形的内角和等于多少度? 十边形呢?
解:设这个多边形的边数为n,根据题意得:
(n-2) ×180=108n
解得:n=5 答:这个多边形是五边形。
练习
4. 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:
如图,四边形ABCD中,
∠A+ ∠C =180°
∠A+∠B+∠C+∠D=(4-2) ×180 °
= 360 °
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360°- 180°
=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
所以
如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是__________
相等或者互补
十二边形的内角和是( ).
一个多边形当边数增加1时,它的内角和增加( ).
一个多边形的内角和是720?,则此多边形共有( )个内角.
如果一个多边形的内角和是1440°,那么这是( )边形.
1800?
180?
六
十
课堂检测
【例1】如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
思考:
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
多边形的外角和
五边形外角和
结论:五边形的外角和等于360°.
-(5-2) × 180°
=360 °
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-五边形内角和
=5×180°
【例2】如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
探究 在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
结论:n边形的外角和等于360°.
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
=n个平角-n边形内角和
= n×180 °
n边形外角和是多少度?
每个内角的度数是
每个外角的度数是
(1)若十二边形的每个内角都相等,那么每个内角是______度.
(2)已知多边形的每个内角都是135度,则这个多边形是_______.
(3)如果某个多边形的内角和等于它的外角和,那么这个多边形的边数是________.
150
八边形
四边形
练习1
练习2: 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360?,
∴ (n-2)?180°=2× 360?.
解得: n=6.
∴这个多边形的边数为6.
1、n边形的内角和等于(n-2)×180°.
??
3、利用类比归纳、转化的学习方法,可以把 多边形问题转化为三角形问题来解决; 外角问题转化为内角来解决.
4、方程的数学思想在几何中有重要的作用.
本节课你学会哪些知识?学会了哪些解决问题的方法?你还有哪些疑问?
2、n边形的外角和等于360°.
课堂小结
谢 谢 观 看!
