2020_2021学年北师大版必修1新教材高中数学单元素养评价五第七章含解析(word版含解析)
文档属性
| 名称 | 2020_2021学年北师大版必修1新教材高中数学单元素养评价五第七章含解析(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 16:35:48 | ||
图片预览




文档简介
单元素养评价(五)(第七章)
(120分钟 150分)
一、选择题(每小题5分,共40分)
1.下列事件是随机事件的是
( )
①同种电荷,互相排斥;②明天是晴天;③自由下落的物体做匀速直线运动;④函数y=ax(a>0且a≠1)在定义域上是增函数.
A.①③
B.①④
C.②④
D.③④
2.从装有红球、白球和黑球各2个的口袋内一次取出2个球,则与事件“两球都为白球”互斥而非对立的事件是以下事件:“①两球都不是白球;②两球恰有一白球;③两球至少有一个白球”中的
( )
A.①②
B.①③
C.②③
D.①②③
3.西周初数学家商高在公元前1000年发现勾股定理的一个特例,勾三,股四,弦五.此发现早于毕达哥拉斯定理五百到六百年,我们把可以构成一个直角三角形三边的一组正整数(a,b,c)称为勾股数.现从(3,4,5),(5,12,13),(6,8,10),(7,24,25),(8,15,17),(9,40,41),(9,12,15),(10,24,26),(15,20,25),(15,36,39)这几组勾股数中随机抽取1组,则被抽出的这组勾股数满足2b=a+c的概率为
( )
A.
B.
C.
D.
4.抛掷一枚质地均匀的骰子,观察掷出的点数,设事件A为“出现奇数点”,事件B为“出现2点”,已知P(A)=,P(B)=,则“出现奇数点或2点”的概率为
( )
A.
B.
C.
D.
5.下列试验属于古典概型的有
( )
①从装有大小、形状完全相同的红、黑、绿各一球的袋子中任意取出一球,取出的球为红色的概率;
②在公交车站候车不超过10分钟的概率;
③同时抛掷两枚硬币,观察出现“两正”“两反”“一正一反”的次数;
A.0个
B.1个
C.2个
D.3个
6.若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为
( )
A.
B.
C.
D.
7.某运动会期间,从来自A大学的2名志愿者和来自B大学的4名志愿者中随机抽取2人到体操比赛场馆服务,至少有一名A大学志愿者的概率是
( )
A.
B.
C.
D.
8.一位家长送孩子去幼儿园的路上要经过4个有红绿灯的路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是,遇到红灯时停留的时间都是2
min.则这位家长送孩子上学到第三个路口时首次遇到红灯的概率为
( )
A.
B.
C.
D.
二、多选题(每小题5分,共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.在一个古典概型中,若两个不同的随机事件A,B发生的概率相等,则称A和B是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”.关于“等概率事件”,以下判断正确的是
( )
A.在同一个古典概型中,所有的样本点之间都是“等概率事件”
B.若一个古典概型的事件总数大于2,则在这个古典概型中除样本点外没有其他“等概率事件”
C.因为所有必然事件的概率都是1,所以任意两个必然事件都是“等概率事件”
D.同时抛掷三枚硬币一次,则事件“仅有一个正面”和“仅有两个正面”是“等概率事件”
10.某超市随机选取1
000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成统计表,其中“√”表示购买,“×”表示未购买.
商品顾客人数
甲
乙
丙
丁
100
√
×
√
√
217
×
√
×
√
200
√
√
√
×
300
√
×
√
×
85
√
×
×
×
98
×
√
×
×
根据表中数据,下列结论正确的是
( )
A.顾客购买乙商品的概率最大
B.顾客同时购买乙和丙的概率约为0.2
C.顾客在甲、乙、丙、丁中同时购买3种商品的概率约为0.3
D.顾客仅购买1种商品的概率不大于0.3
11.某篮球运动员在最近几次参加的比赛中的得分情况如表:
投篮次数
投中两分球的次数
投中三分球的次数
100
55
18
记该运动员在一次投篮中,“投中两分球”为事件A,“投中三分球”为事件B,“没投中”为事件C,用频率估计概率的方法,得到的下述结论中,正确的是
( )
A.P=0.55
B.P=0.18
C.P=0.27
D.P=0.55
12.一个袋子中装有3件正品和1件次品,按以下要求抽取2件产品,其中结论正确的是
( )
A.任取2件,则取出的2件中恰有1件次品的概率是
B.每次抽取1件,不放回抽取两次,样本点总数为16
C.每次抽取1件,不放回抽取两次,则取出的2件中恰有1件次品的概率是
D.每次抽取1件,有放回抽取两次,样本点总数为16
三、填空题(每小题5分,共20分)
13.若A,B是相互独立事件,且P(A)=,P(B)=,则P(A)= ,P()= .?
14.《九章算术》是中国古代数学专著,全书采用问题集的形式,收有246个与生产、生活实践有联系的应用问题,其中“均赋粟”问题讲的是古代劳动人民的赋税问题.现拟编试题如下:已知甲、乙、丙、丁四县向国家交税,则甲必须第一个交且乙不是第三个交的概率为 .?
15.用红、黄、蓝三种不同颜色给图中的3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形颜色都相同的概率是 ,3个矩形颜色都不同的概率是 .?
16.在一次数学考试中,第22题和第23题为选做题,规定每名学生必须且只需在其中选做一题.设4名学生选做这两题的可能性均为.则其中甲、乙2名学生选做同一道题的概率为 ;甲、乙2名学生都选做第22题的概率为 .?
四、解答题(共70分)
17.(10分)某校在教师外出培训学习活动中,在一个月派出的培训人数及其概率如表所示:
派出人数
2人及以下
3
4
5
6人及以上
概率
0.1
0.46
0.3
0.1
0.04
(1)求有4个人或5个人培训的概率;
(2)求至少有3个人培训的概率.
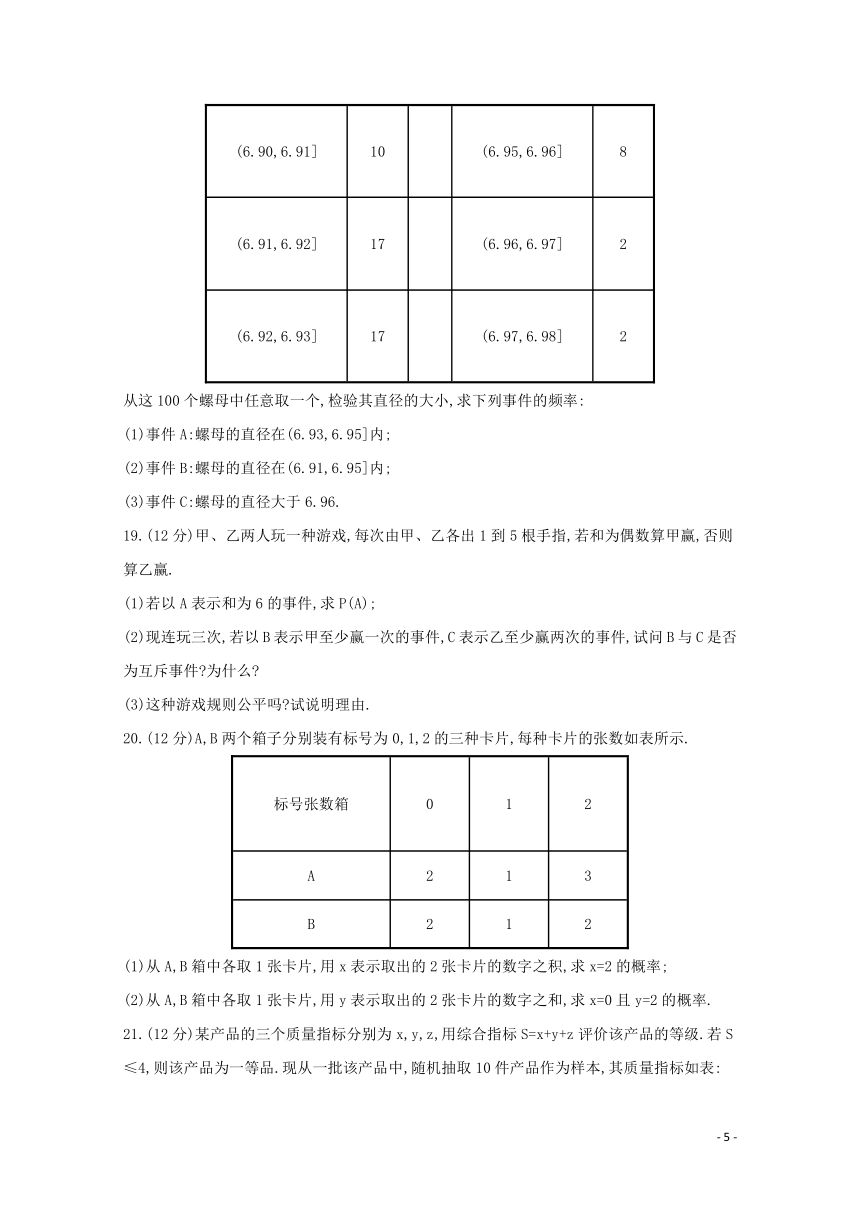
18.(12分)用一台自动机床加工一批螺母,从中抽出100个逐个进行直径(单位:cm)检验,结果如表:
直径(单位:cm)
个数
直径(单位:cm)
个数
[6.88,6.89]
1
(6.93,6.94]
26
(6.89,6.90]
2
(6.94,6.95]
15
(6.90,6.91]
10
(6.95,6.96]
8
(6.91,6.92]
17
(6.96,6.97]
2
(6.92,6.93]
17
(6.97,6.98]
2
从这100个螺母中任意取一个,检验其直径的大小,求下列事件的频率:
(1)事件A:螺母的直径在(6.93,6.95]内;
(2)事件B:螺母的直径在(6.91,6.95]内;
(3)事件C:螺母的直径大于6.96.
19.(12分)甲、乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以A表示和为6的事件,求P(A);
(2)现连玩三次,若以B表示甲至少赢一次的事件,C表示乙至少赢两次的事件,试问B与C是否为互斥事件?为什么?
(3)这种游戏规则公平吗?试说明理由.
20.(12分)A,B两个箱子分别装有标号为0,1,2的三种卡片,每种卡片的张数如表所示.
标号张数箱
0
1
2
A
2
1
3
B
2
1
2
(1)从A,B箱中各取1张卡片,用x表示取出的2张卡片的数字之积,求x=2的概率;
(2)从A,B箱中各取1张卡片,用y表示取出的2张卡片的数字之和,求x=0且y=2的概率.
21.(12分)某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标如表:
产品编号
A1
A2
A3
A4
A5
质量指标(x,y,z)
(1,1,2)
(2,1,1)
(2,2,2)
(1,1,1)
(1,2,1)
产品编号
A6
A7
A8
A9
A10
质量指标(x,y,z)
(1,2,2)
(2,1,1)
(2,2,1)
(1,1,1)
(2,1,2)
(1)利用表中提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中,随机抽取2件产品.
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
22.(12分)某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层随机抽样检查,测得身高(单位:cm)频数分布表如表1、表2.
表1:男生身高频数分布表
身高(cm)
[160,165)
[165,170)
[170,175)
[175,180)
[180,185)
[185,190]
频数
2
5
14
13
4
2
表2:女生身高频数分布表
身高(cm)
[150,155)
[155,160)
[160,165)
[165,170)
[170,175)
[175,180]
频数
1
7
12
6
3
1
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,求这2人中至少有1人的身高在[165,180)内的概率.
单元素养评价(五)(第七章)(答案版)
(120分钟 150分)
一、选择题(每小题5分,共40分)
1.下列事件是随机事件的是
( )
①同种电荷,互相排斥;②明天是晴天;③自由下落的物体做匀速直线运动;④函数y=ax(a>0且a≠1)在定义域上是增函数.
A.①③
B.①④
C.②④
D.③④
【解析】选C.②④是随机事件,①是必然事件,③是不可能事件.
2.从装有红球、白球和黑球各2个的口袋内一次取出2个球,则与事件“两球都为白球”互斥而非对立的事件是以下事件:“①两球都不是白球;②两球恰有一白球;③两球至少有一个白球”中的
( )
A.①②
B.①③
C.②③
D.①②③
【解析】选A.从装有红球、白球和黑球各2个的口袋内一次取出2个球,所有的样本点为:白白,白红,白黑,红红,红黑,黑黑.除“两球都不是白球”外,还有其他事件如白红可能发生,故①与“两球都为白球”互斥但不对立.除“两球都为白球”和“两球恰有一白球”外,还有其他事件,如无白球,故②与“两球都为白球”互斥但不对立.③两球至少有一个白球,其中包含两个都是白球,故不互斥.
3.西周初数学家商高在公元前1000年发现勾股定理的一个特例,勾三,股四,弦五.此发现早于毕达哥拉斯定理五百到六百年,我们把可以构成一个直角三角形三边的一组正整数(a,b,c)称为勾股数.现从(3,4,5),(5,12,13),(6,8,10),(7,24,25),(8,15,17),(9,40,41),(9,12,15),(10,24,26),(15,20,25),(15,36,39)这几组勾股数中随机抽取1组,则被抽出的这组勾股数满足2b=a+c的概率为
( )
A.
B.
C.
D.
【解析】选A.从这10组勾股数随机抽取1组,共10种抽取方法,其中满足2b=a+c的有:(3,4,5),(6,8,10),(9,12,15),(15,20,25),共4种,
故所求概率为P==.
4.抛掷一枚质地均匀的骰子,观察掷出的点数,设事件A为“出现奇数点”,事件B为“出现2点”,已知P(A)=,P(B)=,则“出现奇数点或2点”的概率为
( )
A.
B.
C.
D.
【解析】选D.因为“出现奇数点”与“出现2点”两事件互斥,
所以P=P(A)+P(B)=+=.
5.下列试验属于古典概型的有
( )
①从装有大小、形状完全相同的红、黑、绿各一球的袋子中任意取出一球,取出的球为红色的概率;
②在公交车站候车不超过10分钟的概率;
③同时抛掷两枚硬币,观察出现“两正”“两反”“一正一反”的次数;
A.0个
B.1个
C.2个
D.3个
【解析】选B.古典概型的两个基本特征是有限性和等可能性,①符合两个特征,是古典概型;②中的样本点的个数无限多;对于③,出现“两正”“两反”“一正一反”的可能性不相等,故不是古典概型.
6.若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为
( )
A.
B.
C.
D.
【解析】选D.事件“甲或乙被录用”的对立事件是“甲和乙都未被录用”,从五位学生中选三人的总的样本点的个数为10,“甲和乙都未被录用”只有1种情况,根据古典概型和对立事件的概率公式可得,甲或乙被录用的概率P=1-=.
7.某运动会期间,从来自A大学的2名志愿者和来自B大学的4名志愿者中随机抽取2人到体操比赛场馆服务,至少有一名A大学志愿者的概率是
( )
A.
B.
C.
D.
【解析】选C.用列举法可得样本空间中样本点的总数为15,所求概率的事件包括的样本点的个数为9,
所以P==.
8.一位家长送孩子去幼儿园的路上要经过4个有红绿灯的路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是,遇到红灯时停留的时间都是2
min.则这位家长送孩子上学到第三个路口时首次遇到红灯的概率为
( )
A.
B.
C.
D.
【解析】选C.设“这位家长送孩子上学到第三个路口时首次遇到红灯”为事件A,因为事件A等于事件“这位家长送孩子在第一个路口和第二个路口没有遇到红灯,在第三个路口遇到红灯”,所以事件A的概率为P(A)=××=.
二、多选题(每小题5分,共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.在一个古典概型中,若两个不同的随机事件A,B发生的概率相等,则称A和B是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”.关于“等概率事件”,以下判断正确的是
( )
A.在同一个古典概型中,所有的样本点之间都是“等概率事件”
B.若一个古典概型的事件总数大于2,则在这个古典概型中除样本点外没有其他“等概率事件”
C.因为所有必然事件的概率都是1,所以任意两个必然事件都是“等概率事件”
D.同时抛掷三枚硬币一次,则事件“仅有一个正面”和“仅有两个正面”是“等概率事件”
【解析】选AD.对于A,由古典概型的定义知,所有样本点的概率都相等,故所有样本点之间都是“等概率事件”,故A正确;对于B,如在1,3,5,7,9五个数中,任取两个数,所得和为8和10这两个事件发生的概率相等,故B错误;对于C,由题可知“等概率事件”是针对同一个古典概型的,故C不正确;对于D,同时抛掷三枚硬币一次共有8种不同的结果,其中“仅有一个正面”包含3种结果,其概率为,“仅有两个正面”包含3种结果,其概率为,故这两个事件是“等概率事件”,故D正确.
10.某超市随机选取1
000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成统计表,其中“√”表示购买,“×”表示未购买.
商品顾客人数
甲
乙
丙
丁
100
√
×
√
√
217
×
√
×
√
200
√
√
√
×
300
√
×
√
×
85
√
×
×
×
98
×
√
×
×
根据表中数据,下列结论正确的是
( )
A.顾客购买乙商品的概率最大
B.顾客同时购买乙和丙的概率约为0.2
C.顾客在甲、乙、丙、丁中同时购买3种商品的概率约为0.3
D.顾客仅购买1种商品的概率不大于0.3
【解析】选BCD.对于A,由于购买甲商品的顾客有685位,购买乙商品的顾客有515位,故A错误;
对于B,因为从统计表可以看出,在这1
000位顾客中,有200位顾客同时购买了乙和丙,
所以顾客同时购买乙和丙的概率可以估计为=0.2,故B正确;
对于C,因为从统计表可以看出,在这1
000位顾客中,有100位顾客同时购买了甲、丙、丁,另有200位顾客同时购买了甲、乙、丙,其他顾客最多购买了2种商品,所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为=0.3,故C正确;
对于D,因为从统计表可以看出,在这1
000位顾客中,有183位顾客仅购买1种商品,所以顾客仅购买1种商品的概率可以估计为0.183<0.2,故D正确.
11.某篮球运动员在最近几次参加的比赛中的得分情况如表:
投篮次数
投中两分球的次数
投中三分球的次数
100
55
18
记该运动员在一次投篮中,“投中两分球”为事件A,“投中三分球”为事件B,“没投中”为事件C,用频率估计概率的方法,得到的下述结论中,正确的是
( )
A.P=0.55
B.P=0.18
C.P=0.27
D.P=0.55
【解析】选ABC.由题意可知,P==0.55,P(B)==0.18,
事件A+B与事件C为对立事件,且事件A,B,C互斥,
所以P=1-P=1-P-P=0.27,P(B+C)=P+P=0.45.
12.一个袋子中装有3件正品和1件次品,按以下要求抽取2件产品,其中结论正确的是
( )
A.任取2件,则取出的2件中恰有1件次品的概率是
B.每次抽取1件,不放回抽取两次,样本点总数为16
C.每次抽取1件,不放回抽取两次,则取出的2件中恰有1件次品的概率是
D.每次抽取1件,有放回抽取两次,样本点总数为16
【解析】选ACD.记4件产品分别为1,2,3,a,其中a表示次品.A选项,样本空间Ω={(1,2),(1,3),(1,a),(2,3),(2,a),(3,a)},“恰有1件次品”的样本点为(1,a),(2,a),(3,a),因此其概率P==,A正确;B选项,每次抽取1件,不放回抽取两次,样本空间Ω={(1,2),(1,3),(1,a),(2,1),(2,3),(2,a),(3,1),(3,2),(3,a),(a,1)
(a,2),(a,3)},因此n(Ω)=12,B错误;C选项,“取出的2件中恰有1件次品”的样本点数为6,其概率为,C正确;D选项,每次抽取1件,有放回抽取两次,样本空间Ω={(1,1),(1,2),(1,3),(1,a),(2,1),(2,2),(2,3),(2,a),(3,1),(3,2),
(3,3),(3,a),(a,1),(a,2),(a,3),(a,a)},因此n(Ω)=16,D正确.
三、填空题(每小题5分,共20分)
13.若A,B是相互独立事件,且P(A)=,P(B)=,则P(A)= ,P()= .?
【解析】因为P(A)=,P(B)=,
所以P()=1-P(A)=1-=,P()=1-=.
因为A,B相互独立,所以A与,与相互独立,
所以P(A)=P(A)P()=×=,
P()=P()P()=×=.
答案:
14.《九章算术》是中国古代数学专著,全书采用问题集的形式,收有246个与生产、生活实践有联系的应用问题,其中“均赋粟”问题讲的是古代劳动人民的赋税问题.现拟编试题如下:已知甲、乙、丙、丁四县向国家交税,则甲必须第一个交且乙不是第三个交的概率为 .?
【解析】依题意,所有的样本点为:甲—乙—丙—丁,甲—乙—丁—丙,甲—丙—乙—丁,甲—丙—丁—乙,甲—丁—丙—乙,甲—丁—乙—丙,乙、丙、丁第一个交的情况也各有6种,故总的样本点数有24种,其中满足条件的样本点为:甲—乙—丁—丙,甲—乙—丙—丁,甲—丙—丁—乙,甲—丁—丙—乙,共4种,
故所求概率为=.
答案:
15.用红、黄、蓝三种不同颜色给图中的3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形颜色都相同的概率是 ,3个矩形颜色都不同的概率是 .?
【解析】以“红黄蓝”表示从左到右三个矩形所涂的颜色,则所有的样本点有:红红红、红红黄、红红蓝、红黄红、红黄黄、红黄蓝、红蓝红、红蓝黄、红蓝蓝、黄红红、黄红黄、黄红蓝、黄黄红、黄黄黄、黄黄蓝、黄蓝红、黄蓝黄、黄蓝蓝、蓝红红、蓝红黄、蓝红蓝、蓝黄红、蓝黄黄、蓝黄蓝、蓝蓝红、蓝蓝黄、蓝蓝蓝,共27个样本点,
事件“3个矩形颜色都相同”所包含的样本点有:红红红、黄黄黄、蓝蓝蓝,共3个,所以3个矩形颜色都相同的概率是=.事件“3个矩形颜色都不同”所包含的样本点有:红黄蓝、红蓝黄、黄红蓝、黄蓝红、蓝黄红、蓝红黄,共6个,所以3个矩形颜色都不同的概率是=.
答案:
16.在一次数学考试中,第22题和第23题为选做题,规定每名学生必须且只需在其中选做一题.设4名学生选做这两题的可能性均为.则其中甲、乙2名学生选做同一道题的概率为 ;甲、乙2名学生都选做第22题的概率为 .?
【解析】设事件A表示“甲选做第22题”,事件B表示“乙选做第22题”,
则甲,乙2名学生选做同一道题的事件为“AB+”,且事件A,B相互独立,
所以P(AB+)=P(A)P(B)+P()P()=×+×=.
所以甲、乙2名学生选做同一道题的概率为;
因为P(A)P(B)=×=,
所以甲、乙2名学生都选做第22题的概率为.
答案:
四、解答题(共70分)
17.(10分)某校在教师外出培训学习活动中,在一个月派出的培训人数及其概率如表所示:
派出人数
2人及以下
3
4
5
6人及以上
概率
0.1
0.46
0.3
0.1
0.04
(1)求有4个人或5个人培训的概率;
(2)求至少有3个人培训的概率.
【解析】(1)设“有2人及以下培训”为事件A,“有3人培训”为事件B,“有4人培训”为事件C,“有5人培训”为事件D,“有6人及以上培训”为事件E,所以“有4个人或5个人培训”的事件为事件C或事件D,A,B,C,D,E为互斥事件,根据互斥事件的概率加法公式可知P(C∪D)=P(C)+P(D)=0.3+0.1=0.4.
(2)“至少有3个人培训”的对立事件为“有2人及以下培训”,所以由对立事件的概率可知P=1-P(A)=1-0.1=0.9.
18.(12分)用一台自动机床加工一批螺母,从中抽出100个逐个进行直径(单位:cm)检验,结果如表:
直径(单位:cm)
个数
直径(单位:cm)
个数
[6.88,6.89]
1
(6.93,6.94]
26
(6.89,6.90]
2
(6.94,6.95]
15
(6.90,6.91]
10
(6.95,6.96]
8
(6.91,6.92]
17
(6.96,6.97]
2
(6.92,6.93]
17
(6.97,6.98]
2
从这100个螺母中任意取一个,检验其直径的大小,求下列事件的频率:
(1)事件A:螺母的直径在(6.93,6.95]内;
(2)事件B:螺母的直径在(6.91,6.95]内;
(3)事件C:螺母的直径大于6.96.
【解析】(1)螺母的直径在(6.93,6.95]内的频数为nA=26+15=41,
所以事件A的频率为=0.41.
(2)螺母的直径在(6.91,6.95]内的频数为nB=17+17+26+15=75.
所以事件B的频率为=0.75.
(3)螺母的直径大于6.96的频数为nC=2+2=4,
所以事件C的频率为=0.04.
19.(12分)甲、乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以A表示和为6的事件,求P(A);
(2)现连玩三次,若以B表示甲至少赢一次的事件,C表示乙至少赢两次的事件,试问B与C是否为互斥事件?为什么?
(3)这种游戏规则公平吗?试说明理由.
【解析】(1)甲、乙出手指都有5种可能,因此样本点的总数为5×5=25,事件A包括甲、乙出的手指的情况有(1,5),(5,1),(2,4),(4,2),(3,3)共5种情况,
所以P(A)==.
(2)B与C不是互斥事件.因为事件B与C可以同时发生,如甲赢一次,乙赢两次的事件.
(3)这种游戏规则不公平.和为偶数的样本点的个数为13个,(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),
(5,1),(5,3),(5,5).
所以甲赢的概率为,乙赢的概率为.所以这种游戏规则不公平.
20.(12分)A,B两个箱子分别装有标号为0,1,2的三种卡片,每种卡片的张数如表所示.
标号张数箱
0
1
2
A
2
1
3
B
2
1
2
(1)从A,B箱中各取1张卡片,用x表示取出的2张卡片的数字之积,求x=2的概率;
(2)从A,B箱中各取1张卡片,用y表示取出的2张卡片的数字之和,求x=0且y=2的概率.
【解析】(1)记事件A={从A,B箱中各取1张卡片,2张卡片的数字之积等于2}.
样本点的总个数为6×5=30,事件A包含样本点的个数为5.由古典概型的概率公式得P(A)==.
则x=2的概率为.
(2)记事件B={从A,B箱中各取1张卡片,其数字之和为2且积为0}.
事件B包含的样本点的个数为10.由古典概型的概率公式得P(B)==.
则x=0且y=2的概率为.
21.(12分)某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标如表:
产品编号
A1
A2
A3
A4
A5
质量指标(x,y,z)
(1,1,2)
(2,1,1)
(2,2,2)
(1,1,1)
(1,2,1)
产品编号
A6
A7
A8
A9
A10
质量指标(x,y,z)
(1,2,2)
(2,1,1)
(2,2,1)
(1,1,1)
(2,1,2)
(1)利用表中提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中,随机抽取2件产品.
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
【解析】(1)计算10件产品的综合指标S,如表:
产品编号
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
S
4
4
6
3
4
5
4
5
3
5
其中S≤4的有A1,A2,A4,A5,A7,A9,共6件,
故该样本的一等品率为=0.6,
从而可估计该批产品的一等品率为0.6.
(2)①在该样本的一等品中,随机抽取2件产品的所有可能结果为{A1,A2},{A1,A4},{A1,A5},{A1,A7},{A1,A9},{A2,A4},{A2,A5},{A2,A7},{A2,A9},
{A4,A5},{A4,A7},{A4,A9},{A5,A7},{A5,A9},{A7,A9},共15种.
②在该样本的一等品中,综合指标S等于4的产品编号分别为A1,A2,A5,A7,则事件B发生的所有可能结果为{A1,A2},{A1,A5},{A1,A7},{A2,A5},{A2,A7},{A5,A7},共6种.所以P(B)==.
22.(12分)某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层随机抽样检查,测得身高(单位:cm)频数分布表如表1、表2.
表1:男生身高频数分布表
身高(cm)
[160,165)
[165,170)
[170,175)
[175,180)
[180,185)
[185,190]
频数
2
5
14
13
4
2
表2:女生身高频数分布表
身高(cm)
[150,155)
[155,160)
[160,165)
[165,170)
[170,175)
[175,180]
频数
1
7
12
6
3
1
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,求这2人中至少有1人的身高在[165,180)内的概率.
【解析】(1)设高一女生人数为x,由题中表1和表2可得样本中男、女生人数分别为40,30,
则=,解得x=300.
因此高一女生的人数为300.
(2)由题中表1和表2可得样本中身高在[165,180)的男、女生人数分别为32,10,
其和为42.样本容量为70.
所以样本中该校学生身高在[165,180)的概率为=.
估计该校学生身高在[165,180)的概率为.
(3)由题中表格可知:女生身高在[165,180)的概率为.男生身高在[165,180)的概率为,
所以这2人中至少有1人的身高在[165,180)内的概率为×+×+×=.
PAGE
-
13
-
(120分钟 150分)
一、选择题(每小题5分,共40分)
1.下列事件是随机事件的是
( )
①同种电荷,互相排斥;②明天是晴天;③自由下落的物体做匀速直线运动;④函数y=ax(a>0且a≠1)在定义域上是增函数.
A.①③
B.①④
C.②④
D.③④
2.从装有红球、白球和黑球各2个的口袋内一次取出2个球,则与事件“两球都为白球”互斥而非对立的事件是以下事件:“①两球都不是白球;②两球恰有一白球;③两球至少有一个白球”中的
( )
A.①②
B.①③
C.②③
D.①②③
3.西周初数学家商高在公元前1000年发现勾股定理的一个特例,勾三,股四,弦五.此发现早于毕达哥拉斯定理五百到六百年,我们把可以构成一个直角三角形三边的一组正整数(a,b,c)称为勾股数.现从(3,4,5),(5,12,13),(6,8,10),(7,24,25),(8,15,17),(9,40,41),(9,12,15),(10,24,26),(15,20,25),(15,36,39)这几组勾股数中随机抽取1组,则被抽出的这组勾股数满足2b=a+c的概率为
( )
A.
B.
C.
D.
4.抛掷一枚质地均匀的骰子,观察掷出的点数,设事件A为“出现奇数点”,事件B为“出现2点”,已知P(A)=,P(B)=,则“出现奇数点或2点”的概率为
( )
A.
B.
C.
D.
5.下列试验属于古典概型的有
( )
①从装有大小、形状完全相同的红、黑、绿各一球的袋子中任意取出一球,取出的球为红色的概率;
②在公交车站候车不超过10分钟的概率;
③同时抛掷两枚硬币,观察出现“两正”“两反”“一正一反”的次数;
A.0个
B.1个
C.2个
D.3个
6.若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为
( )
A.
B.
C.
D.
7.某运动会期间,从来自A大学的2名志愿者和来自B大学的4名志愿者中随机抽取2人到体操比赛场馆服务,至少有一名A大学志愿者的概率是
( )
A.
B.
C.
D.
8.一位家长送孩子去幼儿园的路上要经过4个有红绿灯的路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是,遇到红灯时停留的时间都是2
min.则这位家长送孩子上学到第三个路口时首次遇到红灯的概率为
( )
A.
B.
C.
D.
二、多选题(每小题5分,共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.在一个古典概型中,若两个不同的随机事件A,B发生的概率相等,则称A和B是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”.关于“等概率事件”,以下判断正确的是
( )
A.在同一个古典概型中,所有的样本点之间都是“等概率事件”
B.若一个古典概型的事件总数大于2,则在这个古典概型中除样本点外没有其他“等概率事件”
C.因为所有必然事件的概率都是1,所以任意两个必然事件都是“等概率事件”
D.同时抛掷三枚硬币一次,则事件“仅有一个正面”和“仅有两个正面”是“等概率事件”
10.某超市随机选取1
000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成统计表,其中“√”表示购买,“×”表示未购买.
商品顾客人数
甲
乙
丙
丁
100
√
×
√
√
217
×
√
×
√
200
√
√
√
×
300
√
×
√
×
85
√
×
×
×
98
×
√
×
×
根据表中数据,下列结论正确的是
( )
A.顾客购买乙商品的概率最大
B.顾客同时购买乙和丙的概率约为0.2
C.顾客在甲、乙、丙、丁中同时购买3种商品的概率约为0.3
D.顾客仅购买1种商品的概率不大于0.3
11.某篮球运动员在最近几次参加的比赛中的得分情况如表:
投篮次数
投中两分球的次数
投中三分球的次数
100
55
18
记该运动员在一次投篮中,“投中两分球”为事件A,“投中三分球”为事件B,“没投中”为事件C,用频率估计概率的方法,得到的下述结论中,正确的是
( )
A.P=0.55
B.P=0.18
C.P=0.27
D.P=0.55
12.一个袋子中装有3件正品和1件次品,按以下要求抽取2件产品,其中结论正确的是
( )
A.任取2件,则取出的2件中恰有1件次品的概率是
B.每次抽取1件,不放回抽取两次,样本点总数为16
C.每次抽取1件,不放回抽取两次,则取出的2件中恰有1件次品的概率是
D.每次抽取1件,有放回抽取两次,样本点总数为16
三、填空题(每小题5分,共20分)
13.若A,B是相互独立事件,且P(A)=,P(B)=,则P(A)= ,P()= .?
14.《九章算术》是中国古代数学专著,全书采用问题集的形式,收有246个与生产、生活实践有联系的应用问题,其中“均赋粟”问题讲的是古代劳动人民的赋税问题.现拟编试题如下:已知甲、乙、丙、丁四县向国家交税,则甲必须第一个交且乙不是第三个交的概率为 .?
15.用红、黄、蓝三种不同颜色给图中的3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形颜色都相同的概率是 ,3个矩形颜色都不同的概率是 .?
16.在一次数学考试中,第22题和第23题为选做题,规定每名学生必须且只需在其中选做一题.设4名学生选做这两题的可能性均为.则其中甲、乙2名学生选做同一道题的概率为 ;甲、乙2名学生都选做第22题的概率为 .?
四、解答题(共70分)
17.(10分)某校在教师外出培训学习活动中,在一个月派出的培训人数及其概率如表所示:
派出人数
2人及以下
3
4
5
6人及以上
概率
0.1
0.46
0.3
0.1
0.04
(1)求有4个人或5个人培训的概率;
(2)求至少有3个人培训的概率.
18.(12分)用一台自动机床加工一批螺母,从中抽出100个逐个进行直径(单位:cm)检验,结果如表:
直径(单位:cm)
个数
直径(单位:cm)
个数
[6.88,6.89]
1
(6.93,6.94]
26
(6.89,6.90]
2
(6.94,6.95]
15
(6.90,6.91]
10
(6.95,6.96]
8
(6.91,6.92]
17
(6.96,6.97]
2
(6.92,6.93]
17
(6.97,6.98]
2
从这100个螺母中任意取一个,检验其直径的大小,求下列事件的频率:
(1)事件A:螺母的直径在(6.93,6.95]内;
(2)事件B:螺母的直径在(6.91,6.95]内;
(3)事件C:螺母的直径大于6.96.
19.(12分)甲、乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以A表示和为6的事件,求P(A);
(2)现连玩三次,若以B表示甲至少赢一次的事件,C表示乙至少赢两次的事件,试问B与C是否为互斥事件?为什么?
(3)这种游戏规则公平吗?试说明理由.
20.(12分)A,B两个箱子分别装有标号为0,1,2的三种卡片,每种卡片的张数如表所示.
标号张数箱
0
1
2
A
2
1
3
B
2
1
2
(1)从A,B箱中各取1张卡片,用x表示取出的2张卡片的数字之积,求x=2的概率;
(2)从A,B箱中各取1张卡片,用y表示取出的2张卡片的数字之和,求x=0且y=2的概率.
21.(12分)某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标如表:
产品编号
A1
A2
A3
A4
A5
质量指标(x,y,z)
(1,1,2)
(2,1,1)
(2,2,2)
(1,1,1)
(1,2,1)
产品编号
A6
A7
A8
A9
A10
质量指标(x,y,z)
(1,2,2)
(2,1,1)
(2,2,1)
(1,1,1)
(2,1,2)
(1)利用表中提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中,随机抽取2件产品.
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
22.(12分)某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层随机抽样检查,测得身高(单位:cm)频数分布表如表1、表2.
表1:男生身高频数分布表
身高(cm)
[160,165)
[165,170)
[170,175)
[175,180)
[180,185)
[185,190]
频数
2
5
14
13
4
2
表2:女生身高频数分布表
身高(cm)
[150,155)
[155,160)
[160,165)
[165,170)
[170,175)
[175,180]
频数
1
7
12
6
3
1
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,求这2人中至少有1人的身高在[165,180)内的概率.
单元素养评价(五)(第七章)(答案版)
(120分钟 150分)
一、选择题(每小题5分,共40分)
1.下列事件是随机事件的是
( )
①同种电荷,互相排斥;②明天是晴天;③自由下落的物体做匀速直线运动;④函数y=ax(a>0且a≠1)在定义域上是增函数.
A.①③
B.①④
C.②④
D.③④
【解析】选C.②④是随机事件,①是必然事件,③是不可能事件.
2.从装有红球、白球和黑球各2个的口袋内一次取出2个球,则与事件“两球都为白球”互斥而非对立的事件是以下事件:“①两球都不是白球;②两球恰有一白球;③两球至少有一个白球”中的
( )
A.①②
B.①③
C.②③
D.①②③
【解析】选A.从装有红球、白球和黑球各2个的口袋内一次取出2个球,所有的样本点为:白白,白红,白黑,红红,红黑,黑黑.除“两球都不是白球”外,还有其他事件如白红可能发生,故①与“两球都为白球”互斥但不对立.除“两球都为白球”和“两球恰有一白球”外,还有其他事件,如无白球,故②与“两球都为白球”互斥但不对立.③两球至少有一个白球,其中包含两个都是白球,故不互斥.
3.西周初数学家商高在公元前1000年发现勾股定理的一个特例,勾三,股四,弦五.此发现早于毕达哥拉斯定理五百到六百年,我们把可以构成一个直角三角形三边的一组正整数(a,b,c)称为勾股数.现从(3,4,5),(5,12,13),(6,8,10),(7,24,25),(8,15,17),(9,40,41),(9,12,15),(10,24,26),(15,20,25),(15,36,39)这几组勾股数中随机抽取1组,则被抽出的这组勾股数满足2b=a+c的概率为
( )
A.
B.
C.
D.
【解析】选A.从这10组勾股数随机抽取1组,共10种抽取方法,其中满足2b=a+c的有:(3,4,5),(6,8,10),(9,12,15),(15,20,25),共4种,
故所求概率为P==.
4.抛掷一枚质地均匀的骰子,观察掷出的点数,设事件A为“出现奇数点”,事件B为“出现2点”,已知P(A)=,P(B)=,则“出现奇数点或2点”的概率为
( )
A.
B.
C.
D.
【解析】选D.因为“出现奇数点”与“出现2点”两事件互斥,
所以P=P(A)+P(B)=+=.
5.下列试验属于古典概型的有
( )
①从装有大小、形状完全相同的红、黑、绿各一球的袋子中任意取出一球,取出的球为红色的概率;
②在公交车站候车不超过10分钟的概率;
③同时抛掷两枚硬币,观察出现“两正”“两反”“一正一反”的次数;
A.0个
B.1个
C.2个
D.3个
【解析】选B.古典概型的两个基本特征是有限性和等可能性,①符合两个特征,是古典概型;②中的样本点的个数无限多;对于③,出现“两正”“两反”“一正一反”的可能性不相等,故不是古典概型.
6.若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为
( )
A.
B.
C.
D.
【解析】选D.事件“甲或乙被录用”的对立事件是“甲和乙都未被录用”,从五位学生中选三人的总的样本点的个数为10,“甲和乙都未被录用”只有1种情况,根据古典概型和对立事件的概率公式可得,甲或乙被录用的概率P=1-=.
7.某运动会期间,从来自A大学的2名志愿者和来自B大学的4名志愿者中随机抽取2人到体操比赛场馆服务,至少有一名A大学志愿者的概率是
( )
A.
B.
C.
D.
【解析】选C.用列举法可得样本空间中样本点的总数为15,所求概率的事件包括的样本点的个数为9,
所以P==.
8.一位家长送孩子去幼儿园的路上要经过4个有红绿灯的路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是,遇到红灯时停留的时间都是2
min.则这位家长送孩子上学到第三个路口时首次遇到红灯的概率为
( )
A.
B.
C.
D.
【解析】选C.设“这位家长送孩子上学到第三个路口时首次遇到红灯”为事件A,因为事件A等于事件“这位家长送孩子在第一个路口和第二个路口没有遇到红灯,在第三个路口遇到红灯”,所以事件A的概率为P(A)=××=.
二、多选题(每小题5分,共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.在一个古典概型中,若两个不同的随机事件A,B发生的概率相等,则称A和B是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”.关于“等概率事件”,以下判断正确的是
( )
A.在同一个古典概型中,所有的样本点之间都是“等概率事件”
B.若一个古典概型的事件总数大于2,则在这个古典概型中除样本点外没有其他“等概率事件”
C.因为所有必然事件的概率都是1,所以任意两个必然事件都是“等概率事件”
D.同时抛掷三枚硬币一次,则事件“仅有一个正面”和“仅有两个正面”是“等概率事件”
【解析】选AD.对于A,由古典概型的定义知,所有样本点的概率都相等,故所有样本点之间都是“等概率事件”,故A正确;对于B,如在1,3,5,7,9五个数中,任取两个数,所得和为8和10这两个事件发生的概率相等,故B错误;对于C,由题可知“等概率事件”是针对同一个古典概型的,故C不正确;对于D,同时抛掷三枚硬币一次共有8种不同的结果,其中“仅有一个正面”包含3种结果,其概率为,“仅有两个正面”包含3种结果,其概率为,故这两个事件是“等概率事件”,故D正确.
10.某超市随机选取1
000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成统计表,其中“√”表示购买,“×”表示未购买.
商品顾客人数
甲
乙
丙
丁
100
√
×
√
√
217
×
√
×
√
200
√
√
√
×
300
√
×
√
×
85
√
×
×
×
98
×
√
×
×
根据表中数据,下列结论正确的是
( )
A.顾客购买乙商品的概率最大
B.顾客同时购买乙和丙的概率约为0.2
C.顾客在甲、乙、丙、丁中同时购买3种商品的概率约为0.3
D.顾客仅购买1种商品的概率不大于0.3
【解析】选BCD.对于A,由于购买甲商品的顾客有685位,购买乙商品的顾客有515位,故A错误;
对于B,因为从统计表可以看出,在这1
000位顾客中,有200位顾客同时购买了乙和丙,
所以顾客同时购买乙和丙的概率可以估计为=0.2,故B正确;
对于C,因为从统计表可以看出,在这1
000位顾客中,有100位顾客同时购买了甲、丙、丁,另有200位顾客同时购买了甲、乙、丙,其他顾客最多购买了2种商品,所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为=0.3,故C正确;
对于D,因为从统计表可以看出,在这1
000位顾客中,有183位顾客仅购买1种商品,所以顾客仅购买1种商品的概率可以估计为0.183<0.2,故D正确.
11.某篮球运动员在最近几次参加的比赛中的得分情况如表:
投篮次数
投中两分球的次数
投中三分球的次数
100
55
18
记该运动员在一次投篮中,“投中两分球”为事件A,“投中三分球”为事件B,“没投中”为事件C,用频率估计概率的方法,得到的下述结论中,正确的是
( )
A.P=0.55
B.P=0.18
C.P=0.27
D.P=0.55
【解析】选ABC.由题意可知,P==0.55,P(B)==0.18,
事件A+B与事件C为对立事件,且事件A,B,C互斥,
所以P=1-P=1-P-P=0.27,P(B+C)=P+P=0.45.
12.一个袋子中装有3件正品和1件次品,按以下要求抽取2件产品,其中结论正确的是
( )
A.任取2件,则取出的2件中恰有1件次品的概率是
B.每次抽取1件,不放回抽取两次,样本点总数为16
C.每次抽取1件,不放回抽取两次,则取出的2件中恰有1件次品的概率是
D.每次抽取1件,有放回抽取两次,样本点总数为16
【解析】选ACD.记4件产品分别为1,2,3,a,其中a表示次品.A选项,样本空间Ω={(1,2),(1,3),(1,a),(2,3),(2,a),(3,a)},“恰有1件次品”的样本点为(1,a),(2,a),(3,a),因此其概率P==,A正确;B选项,每次抽取1件,不放回抽取两次,样本空间Ω={(1,2),(1,3),(1,a),(2,1),(2,3),(2,a),(3,1),(3,2),(3,a),(a,1)
(a,2),(a,3)},因此n(Ω)=12,B错误;C选项,“取出的2件中恰有1件次品”的样本点数为6,其概率为,C正确;D选项,每次抽取1件,有放回抽取两次,样本空间Ω={(1,1),(1,2),(1,3),(1,a),(2,1),(2,2),(2,3),(2,a),(3,1),(3,2),
(3,3),(3,a),(a,1),(a,2),(a,3),(a,a)},因此n(Ω)=16,D正确.
三、填空题(每小题5分,共20分)
13.若A,B是相互独立事件,且P(A)=,P(B)=,则P(A)= ,P()= .?
【解析】因为P(A)=,P(B)=,
所以P()=1-P(A)=1-=,P()=1-=.
因为A,B相互独立,所以A与,与相互独立,
所以P(A)=P(A)P()=×=,
P()=P()P()=×=.
答案:
14.《九章算术》是中国古代数学专著,全书采用问题集的形式,收有246个与生产、生活实践有联系的应用问题,其中“均赋粟”问题讲的是古代劳动人民的赋税问题.现拟编试题如下:已知甲、乙、丙、丁四县向国家交税,则甲必须第一个交且乙不是第三个交的概率为 .?
【解析】依题意,所有的样本点为:甲—乙—丙—丁,甲—乙—丁—丙,甲—丙—乙—丁,甲—丙—丁—乙,甲—丁—丙—乙,甲—丁—乙—丙,乙、丙、丁第一个交的情况也各有6种,故总的样本点数有24种,其中满足条件的样本点为:甲—乙—丁—丙,甲—乙—丙—丁,甲—丙—丁—乙,甲—丁—丙—乙,共4种,
故所求概率为=.
答案:
15.用红、黄、蓝三种不同颜色给图中的3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形颜色都相同的概率是 ,3个矩形颜色都不同的概率是 .?
【解析】以“红黄蓝”表示从左到右三个矩形所涂的颜色,则所有的样本点有:红红红、红红黄、红红蓝、红黄红、红黄黄、红黄蓝、红蓝红、红蓝黄、红蓝蓝、黄红红、黄红黄、黄红蓝、黄黄红、黄黄黄、黄黄蓝、黄蓝红、黄蓝黄、黄蓝蓝、蓝红红、蓝红黄、蓝红蓝、蓝黄红、蓝黄黄、蓝黄蓝、蓝蓝红、蓝蓝黄、蓝蓝蓝,共27个样本点,
事件“3个矩形颜色都相同”所包含的样本点有:红红红、黄黄黄、蓝蓝蓝,共3个,所以3个矩形颜色都相同的概率是=.事件“3个矩形颜色都不同”所包含的样本点有:红黄蓝、红蓝黄、黄红蓝、黄蓝红、蓝黄红、蓝红黄,共6个,所以3个矩形颜色都不同的概率是=.
答案:
16.在一次数学考试中,第22题和第23题为选做题,规定每名学生必须且只需在其中选做一题.设4名学生选做这两题的可能性均为.则其中甲、乙2名学生选做同一道题的概率为 ;甲、乙2名学生都选做第22题的概率为 .?
【解析】设事件A表示“甲选做第22题”,事件B表示“乙选做第22题”,
则甲,乙2名学生选做同一道题的事件为“AB+”,且事件A,B相互独立,
所以P(AB+)=P(A)P(B)+P()P()=×+×=.
所以甲、乙2名学生选做同一道题的概率为;
因为P(A)P(B)=×=,
所以甲、乙2名学生都选做第22题的概率为.
答案:
四、解答题(共70分)
17.(10分)某校在教师外出培训学习活动中,在一个月派出的培训人数及其概率如表所示:
派出人数
2人及以下
3
4
5
6人及以上
概率
0.1
0.46
0.3
0.1
0.04
(1)求有4个人或5个人培训的概率;
(2)求至少有3个人培训的概率.
【解析】(1)设“有2人及以下培训”为事件A,“有3人培训”为事件B,“有4人培训”为事件C,“有5人培训”为事件D,“有6人及以上培训”为事件E,所以“有4个人或5个人培训”的事件为事件C或事件D,A,B,C,D,E为互斥事件,根据互斥事件的概率加法公式可知P(C∪D)=P(C)+P(D)=0.3+0.1=0.4.
(2)“至少有3个人培训”的对立事件为“有2人及以下培训”,所以由对立事件的概率可知P=1-P(A)=1-0.1=0.9.
18.(12分)用一台自动机床加工一批螺母,从中抽出100个逐个进行直径(单位:cm)检验,结果如表:
直径(单位:cm)
个数
直径(单位:cm)
个数
[6.88,6.89]
1
(6.93,6.94]
26
(6.89,6.90]
2
(6.94,6.95]
15
(6.90,6.91]
10
(6.95,6.96]
8
(6.91,6.92]
17
(6.96,6.97]
2
(6.92,6.93]
17
(6.97,6.98]
2
从这100个螺母中任意取一个,检验其直径的大小,求下列事件的频率:
(1)事件A:螺母的直径在(6.93,6.95]内;
(2)事件B:螺母的直径在(6.91,6.95]内;
(3)事件C:螺母的直径大于6.96.
【解析】(1)螺母的直径在(6.93,6.95]内的频数为nA=26+15=41,
所以事件A的频率为=0.41.
(2)螺母的直径在(6.91,6.95]内的频数为nB=17+17+26+15=75.
所以事件B的频率为=0.75.
(3)螺母的直径大于6.96的频数为nC=2+2=4,
所以事件C的频率为=0.04.
19.(12分)甲、乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以A表示和为6的事件,求P(A);
(2)现连玩三次,若以B表示甲至少赢一次的事件,C表示乙至少赢两次的事件,试问B与C是否为互斥事件?为什么?
(3)这种游戏规则公平吗?试说明理由.
【解析】(1)甲、乙出手指都有5种可能,因此样本点的总数为5×5=25,事件A包括甲、乙出的手指的情况有(1,5),(5,1),(2,4),(4,2),(3,3)共5种情况,
所以P(A)==.
(2)B与C不是互斥事件.因为事件B与C可以同时发生,如甲赢一次,乙赢两次的事件.
(3)这种游戏规则不公平.和为偶数的样本点的个数为13个,(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),
(5,1),(5,3),(5,5).
所以甲赢的概率为,乙赢的概率为.所以这种游戏规则不公平.
20.(12分)A,B两个箱子分别装有标号为0,1,2的三种卡片,每种卡片的张数如表所示.
标号张数箱
0
1
2
A
2
1
3
B
2
1
2
(1)从A,B箱中各取1张卡片,用x表示取出的2张卡片的数字之积,求x=2的概率;
(2)从A,B箱中各取1张卡片,用y表示取出的2张卡片的数字之和,求x=0且y=2的概率.
【解析】(1)记事件A={从A,B箱中各取1张卡片,2张卡片的数字之积等于2}.
样本点的总个数为6×5=30,事件A包含样本点的个数为5.由古典概型的概率公式得P(A)==.
则x=2的概率为.
(2)记事件B={从A,B箱中各取1张卡片,其数字之和为2且积为0}.
事件B包含的样本点的个数为10.由古典概型的概率公式得P(B)==.
则x=0且y=2的概率为.
21.(12分)某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标如表:
产品编号
A1
A2
A3
A4
A5
质量指标(x,y,z)
(1,1,2)
(2,1,1)
(2,2,2)
(1,1,1)
(1,2,1)
产品编号
A6
A7
A8
A9
A10
质量指标(x,y,z)
(1,2,2)
(2,1,1)
(2,2,1)
(1,1,1)
(2,1,2)
(1)利用表中提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中,随机抽取2件产品.
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
【解析】(1)计算10件产品的综合指标S,如表:
产品编号
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
S
4
4
6
3
4
5
4
5
3
5
其中S≤4的有A1,A2,A4,A5,A7,A9,共6件,
故该样本的一等品率为=0.6,
从而可估计该批产品的一等品率为0.6.
(2)①在该样本的一等品中,随机抽取2件产品的所有可能结果为{A1,A2},{A1,A4},{A1,A5},{A1,A7},{A1,A9},{A2,A4},{A2,A5},{A2,A7},{A2,A9},
{A4,A5},{A4,A7},{A4,A9},{A5,A7},{A5,A9},{A7,A9},共15种.
②在该样本的一等品中,综合指标S等于4的产品编号分别为A1,A2,A5,A7,则事件B发生的所有可能结果为{A1,A2},{A1,A5},{A1,A7},{A2,A5},{A2,A7},{A5,A7},共6种.所以P(B)==.
22.(12分)某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层随机抽样检查,测得身高(单位:cm)频数分布表如表1、表2.
表1:男生身高频数分布表
身高(cm)
[160,165)
[165,170)
[170,175)
[175,180)
[180,185)
[185,190]
频数
2
5
14
13
4
2
表2:女生身高频数分布表
身高(cm)
[150,155)
[155,160)
[160,165)
[165,170)
[170,175)
[175,180]
频数
1
7
12
6
3
1
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,求这2人中至少有1人的身高在[165,180)内的概率.
【解析】(1)设高一女生人数为x,由题中表1和表2可得样本中男、女生人数分别为40,30,
则=,解得x=300.
因此高一女生的人数为300.
(2)由题中表1和表2可得样本中身高在[165,180)的男、女生人数分别为32,10,
其和为42.样本容量为70.
所以样本中该校学生身高在[165,180)的概率为=.
估计该校学生身高在[165,180)的概率为.
(3)由题中表格可知:女生身高在[165,180)的概率为.男生身高在[165,180)的概率为,
所以这2人中至少有1人的身高在[165,180)内的概率为×+×+×=.
PAGE
-
13
-
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
