人教版小学数学六年级上册课件第五单元 圆 练习十五(20张ppt)
文档属性
| 名称 | 人教版小学数学六年级上册课件第五单元 圆 练习十五(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 12:13:37 | ||
图片预览







文档简介
圆
5
练习十五
义务教育人教版六年级上册
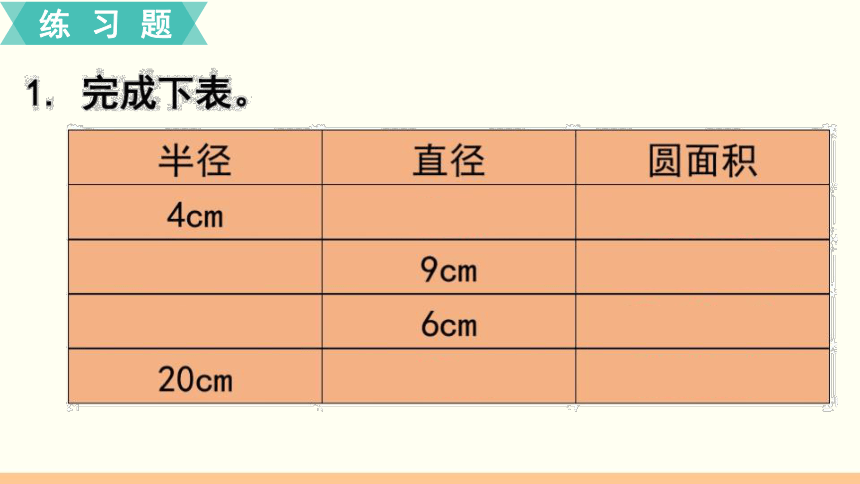
练习题
练习题
练习题
练习题
5.下图是一块玉璧,外直径18cm,内直径
7cm,这块玉璧的面积是多少?
3.14×[(18÷2)2-(7÷2)2]
=3.14×(81-12.25)
=3.14×68.75
=215.875(cm2)
答:这块玉璧的面积是215.875平方厘米。
练习题
6.下图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。
答:阴影部分面积为84.78平方厘米。
练习题
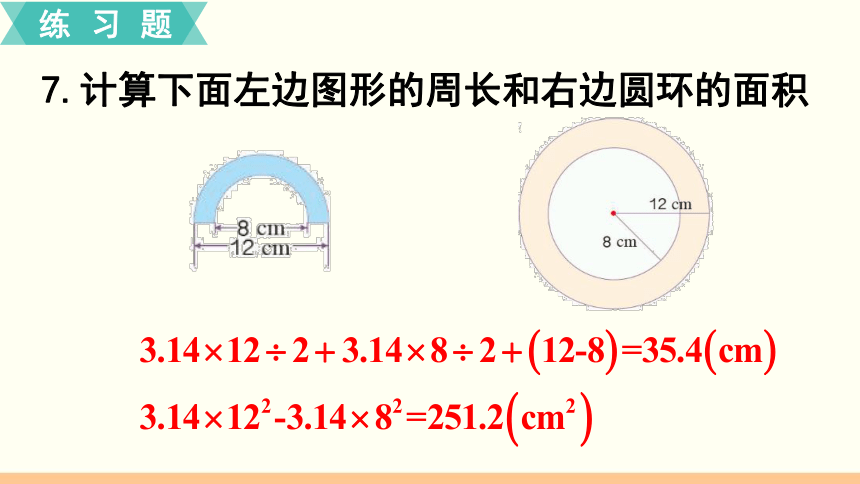
7.计算下面左边图形的周长和右边圆环的面积
练习题
练习题
国筒形卫生纸的横截面是个圆环。
拧螺丝时,金属垫片基本是圆环形的。
练习题
10.一个运动场如右图,两端是半圆形,中间
是长方形。这个运动场的周长是多少米?
面积是多少平方米?
周长: 3.14×32×2 + 100×2
= 400.96(米)
面积:3.14×32? + 32×2×100= 9615.36(平方米)
练习题
答:这个运动场的周长是400.96米;
面积是9615.36平方米。
练习题
练习题
12.土楼是福建、广东等地区的一种建筑形式,被列
入“世界物质文化名录”,土楼的外围形状有圆形、
方形、椭圆等。有两座地面是圆环形的土楼,其中
一座外直径34m,内直径14m;另一座外直径26m,内
直径也是4m。两座土楼的房屋占地面积相差多少?
3.14×[(34÷2)? -(14÷2)? ]=753.6(m? )
3.14×[(26÷2)? -(14÷2)? ]=376.8(m? )
相差面积:753.6-376.8=376.8(m2)
答:两座土楼的房屋占地面积相差376.8m? 。
13.一个圆的周长是62.8m,半径增加了2m后,
面积增加了多少?
62.8÷3.14÷2=10(m)
10+2=12(m)
3.14x12?-3.14×10?=138.16(m?)
答:面积增加了138.16平方米。
练习题
练习题
3分线
6.75m
1.575m
练习题
3分线
6.75m
1.575m
练习题
你发现了什么?请你自己再任意设定一个正方形的边长,在正方形中画一个最大的国,看看是否也能得出相同的结论。
16.有一根绳子长是31.4m,小红、小东和小林分别想用这根绳子在操场上围出一块地。怎样围面积最大?
在周长相等时,围成圆的面积最大。
我想
我想围成正方形
我想
我想围成圆形
练习题
练习题
答:当周长一定时,所有图形中圆的面积最大。
蒙古包的底面做成圆形的,可以使居住的面积最大,
绝大多数的根和茎的横截面是圆形的,可以最大面积
地吸收水分。(合理即可)
17.为什么草原上蒙古包的底面是圆形的?为什么绝大
多数的根和茎的横截面是圆形的?请你试着从数学
的角度解释一下。
5
练习十五
义务教育人教版六年级上册
练习题
练习题
练习题
练习题
5.下图是一块玉璧,外直径18cm,内直径
7cm,这块玉璧的面积是多少?
3.14×[(18÷2)2-(7÷2)2]
=3.14×(81-12.25)
=3.14×68.75
=215.875(cm2)
答:这块玉璧的面积是215.875平方厘米。
练习题
6.下图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。
答:阴影部分面积为84.78平方厘米。
练习题
7.计算下面左边图形的周长和右边圆环的面积
练习题
练习题
国筒形卫生纸的横截面是个圆环。
拧螺丝时,金属垫片基本是圆环形的。
练习题
10.一个运动场如右图,两端是半圆形,中间
是长方形。这个运动场的周长是多少米?
面积是多少平方米?
周长: 3.14×32×2 + 100×2
= 400.96(米)
面积:3.14×32? + 32×2×100= 9615.36(平方米)
练习题
答:这个运动场的周长是400.96米;
面积是9615.36平方米。
练习题
练习题
12.土楼是福建、广东等地区的一种建筑形式,被列
入“世界物质文化名录”,土楼的外围形状有圆形、
方形、椭圆等。有两座地面是圆环形的土楼,其中
一座外直径34m,内直径14m;另一座外直径26m,内
直径也是4m。两座土楼的房屋占地面积相差多少?
3.14×[(34÷2)? -(14÷2)? ]=753.6(m? )
3.14×[(26÷2)? -(14÷2)? ]=376.8(m? )
相差面积:753.6-376.8=376.8(m2)
答:两座土楼的房屋占地面积相差376.8m? 。
13.一个圆的周长是62.8m,半径增加了2m后,
面积增加了多少?
62.8÷3.14÷2=10(m)
10+2=12(m)
3.14x12?-3.14×10?=138.16(m?)
答:面积增加了138.16平方米。
练习题
练习题
3分线
6.75m
1.575m
练习题
3分线
6.75m
1.575m
练习题
你发现了什么?请你自己再任意设定一个正方形的边长,在正方形中画一个最大的国,看看是否也能得出相同的结论。
16.有一根绳子长是31.4m,小红、小东和小林分别想用这根绳子在操场上围出一块地。怎样围面积最大?
在周长相等时,围成圆的面积最大。
我想
我想围成正方形
我想
我想围成圆形
练习题
练习题
答:当周长一定时,所有图形中圆的面积最大。
蒙古包的底面做成圆形的,可以使居住的面积最大,
绝大多数的根和茎的横截面是圆形的,可以最大面积
地吸收水分。(合理即可)
17.为什么草原上蒙古包的底面是圆形的?为什么绝大
多数的根和茎的横截面是圆形的?请你试着从数学
的角度解释一下。
