4.4.3 一次函数的应用(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 4.4.3 一次函数的应用(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 717.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 18:23:13 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第四章一次函数
4.4
一次函数的应用
第3课时
一次函数的应用(3)
【知识清单】
1、一般地,如果两个变量对应数值的差之比是一个常数k,那么这两个变量之间是一次函数关系.事实上,如果y、x是两个变量,x0、y0是它们的一组对应值(x0、y0均为常数),且(k是常数,且k≠0),那么y=kx+(y0-kx0),其中k、x0、y0均为常数.
2、若两条直线y1=k1x+b1与y2=k2x+b2相交于点(x0、y0),当x=x0时,则y1=y2=y0;
3、从图象上看:对同一自变量来说,函数图像在上方,说明函数值大;反之函数值小.
【经典例题】
【例题】1、我市某工厂要印制工人手册,有甲、乙两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每本定价6元的8.5折收费,另收2400元制版费;乙厂的优惠条件是:按每本定价6元的价格不变,而制版费2400元则按4折优惠.且甲、乙两厂都规定:一次印刷数量至少是600份.(1)分别求两个印刷厂收费y(元)与印刷数量x(份)的函数关系,并指出自变量x的取值范围.(2)如果这个工厂要印制3000份工人手册.那么应当选择哪一个厂?需要多少费用?
【考点】一次函数的应用.
【分析】(1)根据题意分别列出两个印刷厂收费y(元)与印刷数量x(份)的函数关系式即可;
(2)将x=3000代入两个函数关系式,求得y甲、?y乙,然后根据y甲、?y乙的大小进行判断即可.
【解答】解:(1)y甲=6×0.85x+2400=5.1x+2400(x≥600,且x是整数),;
???
?
?
?
y乙=6x+2400×0.4=6x+960(x≥600,且x是整数);
(2)当x=3000时,y甲=5.1x+2400=5.1×3000+2400=17700,
y乙=6x+960=6×3000+960=18960.
∵17700<18960,
∴印3000份工人手册,应选择甲厂,费用是17700元.
【点评】本题主要考查了一次函数的实际应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义,列出两个函数关系式以及将自变量x的取值代入是解决问题的关键.
【例题】2、已知A、B两地相距90km,甲、乙两人沿同一条公路从A地出发到B地,甲骑摩托车,乙骑自行车,BC、OA分别表示甲、乙两人离开A的距离s(km)与时间t(h)的函数关系.根据图象,回答下列问题:
(1)______比______晚出发______h;
(2)甲到达B地时,乙距B地还有____km,乙还需_____h到达B地;
(3)甲的速度是______km/h,乙的速度是______km/h.
【考点】一次函数的应用.
【分析】(1)根据横轴可得乙出发2小时后甲才出发;
(2)根据点C、A的纵坐标解答;(3)根据速度=路程÷时间,进行计算即可得解.
【解答】(1)由图可知,甲比乙晚出发2小时;
(2)根据C(4,90),D
(4,60),甲到达B地时,乙距B地还有30km,乙还需2h到达
B地;
(3)甲的速度==45km/h,乙的速度==15km/h.
故答案为:(1)甲,乙,2;(2)30,2;(3)45,15.
【点评】本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,准确识图并获取信息是解题的关键.
【夯实基础】
1、某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数y=kx600图象确定,则旅客可携带的免费行李的最大质量为( )
A.20kg
B.25kg
C.30kg
D.50kg
2、如图所示,甲、乙两人分别从A、B两地同时出发相向而行,他们在点P相遇,两条线段l1、
l2分别表示甲、乙离B地的距离y(km)与已用时间x(h)之间的关系,则甲、乙行走的速
度分别是( )
A、5km/h和3km/h
B、4km/h和4km/h
C、4km/h和5km/h
D、5km/h和4km/h
3、小亮与爸爸相约去离家24km的地方登山,小亮7:00从家出发,骑自行车前往,爸爸7:30
从家出发,骑摩托车前往,小亮和爸爸的行进路程s(km)与时间t(时)的函数图象如图所
示,则下列说法中错误的有( )
①小亮骑自行车的平均速度是12km/h;②爸爸与小亮的平均速度差为4km/h;③爸爸比小亮
提前0.5小时达到登山处;
④爸爸在距家12km处与小亮相遇;
⑤爸爸8分钟前的速度比小亮的慢,8分钟后的速度比小亮的快.
A.
1个
B.
2个
C.
3个
D.
4个
4、如图,某单位需要用车,准备和一个体车主或一国有出租车公司其中的一家签订合同.设汽车每月行驶x
km,应付给个体车主的月租费是y1
元,付给国有出租车公司的月租费是y2
元,y1
,y2
分别与x之间的函数关系图象是如图的两条直线如图所示:如果这个单位估计每月行驶的路程为3500
km,为使费用最少则应租(
)的车合算?
A.个体车主
B.出租车公司
C.个体车主和出租车公司一样
D.无法确定
5、某市内出租车行程3km以内(含3km)起步收费为6元,行程超过3km时,每超过1km,加收1.6元,写出行程大于3km时收费y(元)与里程x(km)的函数关系式
,并指明它是什么函数
,以及自变量的取值范围
.
6、在一次短池自由泳比赛中,甲、乙两名运动员同时参加了这项比赛,游程s(米)与时间t(秒)的关系如图所示,根据图象提供的信息,完成下列填空:这是一项
m的游泳比赛;甲乙两名运动员中
先到达终点.
7、(1)
若直线y=-2x+a和直线y=2x+b的交点坐标为(m,6),则a+b=______.
(2)
图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y(元)与通话时间t(分钟)之间的关系图像.
从图像知,通话2分钟需付的电话费是
元,
通话10分钟需付的电话费是
元.
8、声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)的关系如下表:
气温x(℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
①观察上表,气温每升高5℃,音速如何变化?
②求出y与x之间的表达式;
③气温x=25℃时,某人看到闪电6秒后才听到雷声,那么此人与打雷位置的距离有多远?
9、某生物小组观察一颗20cm高的玉米苗的生长过程,这颗玉米生长高度y(厘米)与时间x(天)的关系,并画出如图所示的图象(AB是线段,直线BC平行x轴).
(1)从观察时起这颗玉米,多少天以后停止长高?
(2)求直线AB的解析式,并求这颗玉米最高长多少厘米?
【提优特训】
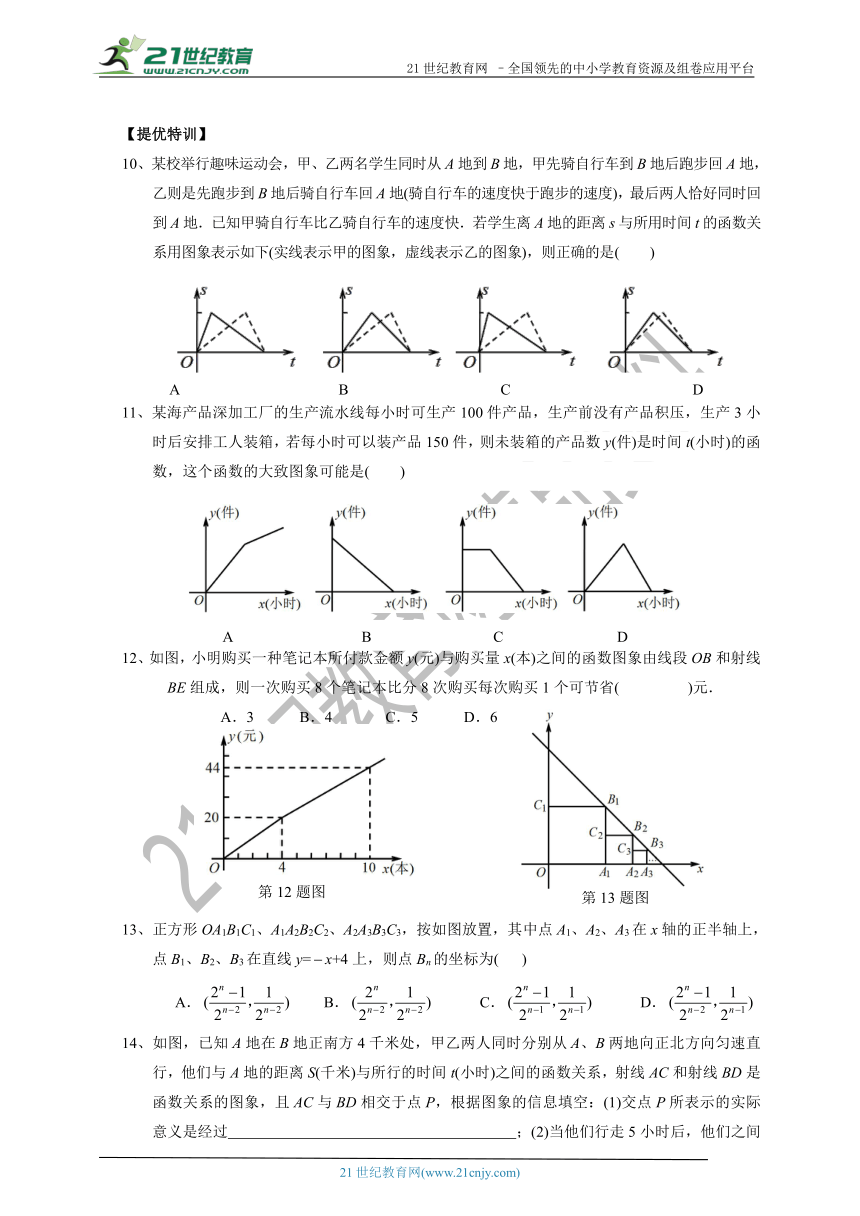
10、某校举行趣味运动会,甲、乙两名学生同时从A地到B地,甲先骑自行车到B地后跑步回A地,乙则是先跑步到B地后骑自行车回A地(骑自行车的速度快于跑步的速度),最后两人恰好同时回到A地.已知甲骑自行车比乙骑自行车的速度快.若学生离A地的距离s与所用时间t的函数关系用图象表示如下(实线表示甲的图象,虚线表示乙的图象),则正确的是( )
11、某海产品深加工厂的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排工人装箱,若每小时可以装产品150件,则未装箱的产品数y(件)是时间t(小时)的函数,这个函数的大致图象可能是( )
12、如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省(
)元.
A.3
B.4
C.5
D.6
13、正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=x+4上,则点Bn的坐标为(
)
A.
B.
C.
D.
14、如图,已知A地在B地正南方4千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系,射线AC和射线BD是函数关系的图象,且AC与BD相交于点P,根据图象的信息填空:(1)交点P所表示的实际意义是经过
;(2)当他们行走5小时后,他们之间的距离为
千米.
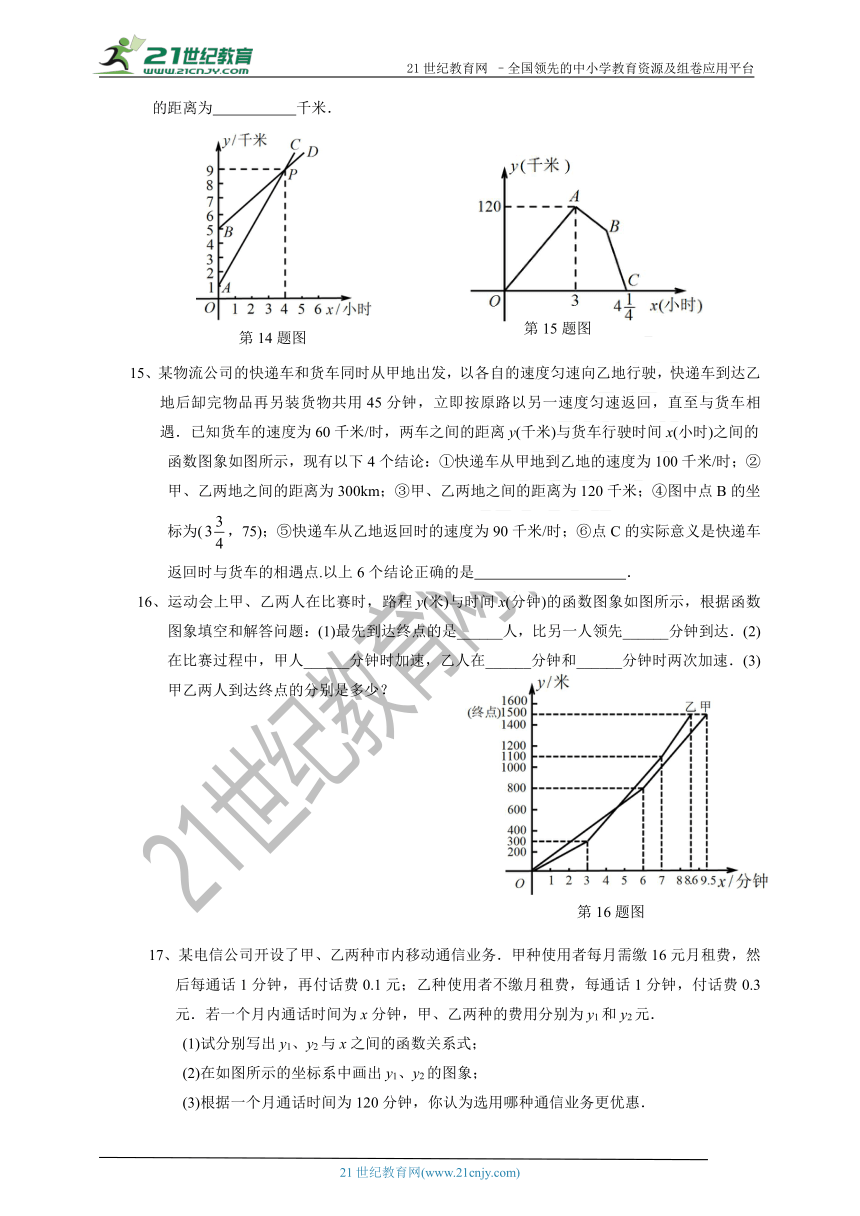
15、某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的
函数图象如图所示,现有以下4个结论:①快递车从甲地到乙地的速度为100千米/时;②甲、乙两地之间的距离为300km;③甲、乙两地之间的距离为120千米;④图中点B的坐标为(,75);⑤快递车从乙地返回时的速度为90千米/时;⑥点C的实际意义是快递车返回时与货车的相遇点.以上6个结论正确的是
.
16、运动会上甲、乙两人在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:(1)最先到达终点的是______人,比另一人领先______分钟到达.(2)在比赛过程中,甲人______分钟时加速,乙人在______分钟和______分钟时两次加速.(3)甲乙两人到达终点的分别是多少?
?17、某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴16元月租费,然后每通话1分钟,再付话费0.1元;乙种使用者不缴月租费,每通话1分钟,付话费0.3元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.
(1)试分别写出y1、y2与x之间的函数关系式;
(2)在如图所示的坐标系中画出y1、y2的图象;
(3)根据一个月通话时间为120分钟,你认为选用哪种通信业务更优惠.
18、如图,直线l1、l2相交于点P,点P的坐标为(3,4)l1分别与x轴、y轴相交于点A、B,l2与y
轴的交点坐标为C(0,3),结合图像解答下列问题:
(1)求出直线l2表示的一次函数的表达式;
(2)若△PBC的面积为6.9个平方单位,求出直线l1表示的一次函数的表达式;
(3)已知点Q在x轴上,△PQA
与△PDA的面积分别为S△PQA与
S△PDA,且S△PQA=
2S
△PDA,求点Q的坐标.
【中考链接】
19、(2019?宜宾)如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.
乙前4秒行驶的路程为48米
B.
在0到8秒内甲的速度每秒增加4米/秒
C.
两车到第3秒时行驶的路程相等
D.
在4至8秒内甲的速度都大于乙的速度
20、(2019?乌鲁木齐)某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是
A.8.4小时
B.8.6小时
C.8.8小时
D.9小时
21、(2019?大连)甲、乙两人沿同一条直路走步,如果两人分别从这条路上的A,B两处同时出发,都以不变的速度相向而行,图1的甲离开A处后行走的路程y(单位:m)与行走的时间x(单位:min)的函数图象,图2是甲、乙两人之间的距离(单位:m)与甲行走的时间x(单位:min)的函数图象,则ab=
.
参考答案
1、A
2、D
3、B
4、A
5、y=1.6x+2,一次函数,x≥3
6、50,甲
7、(1)2.6,
(2)3.1
10、C
11、D
12、B
13、A
14、4小时后,甲乙两人在距离A地8千米处相遇,1
15、①②④⑤⑥
19、C
20、C
21、
8、声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)的关系如下表:
气温x(℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
①观察上表,气温每升高5℃,音速如何变化?
②求出y与x之间的表达式;
③气温x=25℃时,某人看到闪电6秒后才听到雷声,那么此人与打雷位置的距离有多远?
解:①由表可知,温度每上升5℃,音速增加3m/s;
②设y与x之间的表达式为y=kx+b,
∵根据题意,将x=0,y=331;x=5,y=334,代入y=kx+b得,
b=331,5x+b=334,
解得,x==0.6,b=331,
∴y与x之间的表达式为y=0.6x+331;
③当x=25时,y=0.6×25+331=346(m/s),
距离为:346×6=2076米,
∴此人与打雷位置的距离2076米.
9、某生物小组观察一颗20cm高的玉米苗的生长过程,这颗玉米生长高度y(厘米)与时间x(天)的关系,并画出如图所示的图象(AB是线段,直线BC平行x轴).
(1)从观察时起这颗玉米,多少天以后停止长高?
(2)求直线AB的解析式,并求这颗玉米最高长多少厘米?
解:(1)∵BC∥x轴,
∴从第70天开始这颗玉米的高度不变.
答:这颗玉米从栽种起,70天以后停止长高.
(2)设直线AB的解析式为y=kx+b(k≠0),
∵经过点A(0,20),B(25,75),
∴由题意得,
解得,
∴直线AB的解析式为(0当x=70时,(
cm).
答:直线AB的解析式为(016、运动会上甲、乙两人在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:(1)最先到达终点的是______人,比另一人领先______分钟到达.(2)在比赛过程中,甲人______分钟时加速,乙人在______分钟和______分钟时两次加速.(3)甲乙两人到达终点的分别是多少?
(1)根据图象可以得到最先到达终点的是乙,
比乙队领先9.5-8.6=0.9分钟;
(2)根据图象可得甲人在第6分钟加速,
乙人在第2分钟和第7分钟时两次加速;
(3)甲人到达终点的速度为:
(1500800)÷(9.56)=200(米/分钟),
乙人到达终点的速度为:
(15001100)÷(8.67)=250(米/分钟).
?17、某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴16元月租费,然后每通话1分钟,再付话费0.1元;乙种使用者不缴月租费,每通话1分钟,付话费0.3元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.
(1)试分别写出y1、y2与x之间的函数关系式;
(2)在如图所示的坐标系中画出y1、y2的图象;
(3)根据一个月通话时间为120分钟,你认为选用哪种通信业务更优惠.
解:(1)由题意得:y1=0.1x+18(x≥0),y2=0.3x(x≥0);
(2)如图所示:
(3)当x=120分钟时,y1=0.1x+18=0.1×120+18=30,
y2=0.3x=0.3×120=36,
∵30<36.
∴当通话时间为120分钟时,选择甲种业务更优惠.
18、如图,直线l1、l2相交于点P,点P的坐标为(3,4)l1分别与x轴、y轴相交于点A、B,l2与y
轴的交点坐标为C(0,3),结合图像解答下列问题:
(1)求出直线l2表示的一次函数的表达式;
(2)若△PBC的面积为6.9个平方单位,求出直线l1表示的一次函数的表达式;
(3)已知点Q在x轴上,△PQA
与△PDA的面积分别为S△PQA与
S△PDA,且S△PQA=
2S
△PDA,求点Q的坐标.
解:(1)设直线l2的解析式为y=kx+b,???则由图象过点(0,3)和(3,4)得,
?b=3,3k+b=4,解得,k=,
?b=3,
∴直线l2表达式y=x3;
(2)∵△PBC的面积为6.9个平方单位,
∴S△PBC=,即=6.9,
解得BC=4.6,
∵点C的坐标为(0,3),
∴OC=3,
OB=BCOC=4.63=1.6,
∴点B的坐标为(0,1.6)
设直线l1的解析式为y=mx+n,?
将点P(3,4)和点B(0,1.6)代入y=mx+n得,
3m+n=4,n=1.6,
解得m=0.8=,
n=1.6=,
直线l1表达式y=x+;
?
(3)令y=x3=0和y=x+=0
解得x=和x=2,
∴点A、D的坐标分别为(2,0)、(,0),
∴AD=AO+OD=2+=,
∵S△PQA=2S
△PDA,且△PQA
与△PDA是同高的三角形,
∴AQ=2AD=2×=,
∴AD=DQ=,
∴=,2+=,
∴点Q的坐标为(,0)或(,0).
第17题图
第17题图
第16题图
第16题图
第7(2)题图
第16题图
第15题图
第13题图
例题2图
第20题图
第3题图
第17题图
第18题图
第12题图
第3题图
第1题图
第9题图
第18题图
第4题图
第21题图1
第21题图2
第19题图
第14题图
第6题图
A
B
C
D
第17题图
第9题图
A
B
C
D
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学上册第四章一次函数
4.4
一次函数的应用
第3课时
一次函数的应用(3)
【知识清单】
1、一般地,如果两个变量对应数值的差之比是一个常数k,那么这两个变量之间是一次函数关系.事实上,如果y、x是两个变量,x0、y0是它们的一组对应值(x0、y0均为常数),且(k是常数,且k≠0),那么y=kx+(y0-kx0),其中k、x0、y0均为常数.
2、若两条直线y1=k1x+b1与y2=k2x+b2相交于点(x0、y0),当x=x0时,则y1=y2=y0;
3、从图象上看:对同一自变量来说,函数图像在上方,说明函数值大;反之函数值小.
【经典例题】
【例题】1、我市某工厂要印制工人手册,有甲、乙两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每本定价6元的8.5折收费,另收2400元制版费;乙厂的优惠条件是:按每本定价6元的价格不变,而制版费2400元则按4折优惠.且甲、乙两厂都规定:一次印刷数量至少是600份.(1)分别求两个印刷厂收费y(元)与印刷数量x(份)的函数关系,并指出自变量x的取值范围.(2)如果这个工厂要印制3000份工人手册.那么应当选择哪一个厂?需要多少费用?
【考点】一次函数的应用.
【分析】(1)根据题意分别列出两个印刷厂收费y(元)与印刷数量x(份)的函数关系式即可;
(2)将x=3000代入两个函数关系式,求得y甲、?y乙,然后根据y甲、?y乙的大小进行判断即可.
【解答】解:(1)y甲=6×0.85x+2400=5.1x+2400(x≥600,且x是整数),;
???
?
?
?
y乙=6x+2400×0.4=6x+960(x≥600,且x是整数);
(2)当x=3000时,y甲=5.1x+2400=5.1×3000+2400=17700,
y乙=6x+960=6×3000+960=18960.
∵17700<18960,
∴印3000份工人手册,应选择甲厂,费用是17700元.
【点评】本题主要考查了一次函数的实际应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义,列出两个函数关系式以及将自变量x的取值代入是解决问题的关键.
【例题】2、已知A、B两地相距90km,甲、乙两人沿同一条公路从A地出发到B地,甲骑摩托车,乙骑自行车,BC、OA分别表示甲、乙两人离开A的距离s(km)与时间t(h)的函数关系.根据图象,回答下列问题:
(1)______比______晚出发______h;
(2)甲到达B地时,乙距B地还有____km,乙还需_____h到达B地;
(3)甲的速度是______km/h,乙的速度是______km/h.
【考点】一次函数的应用.
【分析】(1)根据横轴可得乙出发2小时后甲才出发;
(2)根据点C、A的纵坐标解答;(3)根据速度=路程÷时间,进行计算即可得解.
【解答】(1)由图可知,甲比乙晚出发2小时;
(2)根据C(4,90),D
(4,60),甲到达B地时,乙距B地还有30km,乙还需2h到达
B地;
(3)甲的速度==45km/h,乙的速度==15km/h.
故答案为:(1)甲,乙,2;(2)30,2;(3)45,15.
【点评】本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,准确识图并获取信息是解题的关键.
【夯实基础】
1、某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数y=kx600图象确定,则旅客可携带的免费行李的最大质量为( )
A.20kg
B.25kg
C.30kg
D.50kg
2、如图所示,甲、乙两人分别从A、B两地同时出发相向而行,他们在点P相遇,两条线段l1、
l2分别表示甲、乙离B地的距离y(km)与已用时间x(h)之间的关系,则甲、乙行走的速
度分别是( )
A、5km/h和3km/h
B、4km/h和4km/h
C、4km/h和5km/h
D、5km/h和4km/h
3、小亮与爸爸相约去离家24km的地方登山,小亮7:00从家出发,骑自行车前往,爸爸7:30
从家出发,骑摩托车前往,小亮和爸爸的行进路程s(km)与时间t(时)的函数图象如图所
示,则下列说法中错误的有( )
①小亮骑自行车的平均速度是12km/h;②爸爸与小亮的平均速度差为4km/h;③爸爸比小亮
提前0.5小时达到登山处;
④爸爸在距家12km处与小亮相遇;
⑤爸爸8分钟前的速度比小亮的慢,8分钟后的速度比小亮的快.
A.
1个
B.
2个
C.
3个
D.
4个
4、如图,某单位需要用车,准备和一个体车主或一国有出租车公司其中的一家签订合同.设汽车每月行驶x
km,应付给个体车主的月租费是y1
元,付给国有出租车公司的月租费是y2
元,y1
,y2
分别与x之间的函数关系图象是如图的两条直线如图所示:如果这个单位估计每月行驶的路程为3500
km,为使费用最少则应租(
)的车合算?
A.个体车主
B.出租车公司
C.个体车主和出租车公司一样
D.无法确定
5、某市内出租车行程3km以内(含3km)起步收费为6元,行程超过3km时,每超过1km,加收1.6元,写出行程大于3km时收费y(元)与里程x(km)的函数关系式
,并指明它是什么函数
,以及自变量的取值范围
.
6、在一次短池自由泳比赛中,甲、乙两名运动员同时参加了这项比赛,游程s(米)与时间t(秒)的关系如图所示,根据图象提供的信息,完成下列填空:这是一项
m的游泳比赛;甲乙两名运动员中
先到达终点.
7、(1)
若直线y=-2x+a和直线y=2x+b的交点坐标为(m,6),则a+b=______.
(2)
图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y(元)与通话时间t(分钟)之间的关系图像.
从图像知,通话2分钟需付的电话费是
元,
通话10分钟需付的电话费是
元.
8、声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)的关系如下表:
气温x(℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
①观察上表,气温每升高5℃,音速如何变化?
②求出y与x之间的表达式;
③气温x=25℃时,某人看到闪电6秒后才听到雷声,那么此人与打雷位置的距离有多远?
9、某生物小组观察一颗20cm高的玉米苗的生长过程,这颗玉米生长高度y(厘米)与时间x(天)的关系,并画出如图所示的图象(AB是线段,直线BC平行x轴).
(1)从观察时起这颗玉米,多少天以后停止长高?
(2)求直线AB的解析式,并求这颗玉米最高长多少厘米?
【提优特训】
10、某校举行趣味运动会,甲、乙两名学生同时从A地到B地,甲先骑自行车到B地后跑步回A地,乙则是先跑步到B地后骑自行车回A地(骑自行车的速度快于跑步的速度),最后两人恰好同时回到A地.已知甲骑自行车比乙骑自行车的速度快.若学生离A地的距离s与所用时间t的函数关系用图象表示如下(实线表示甲的图象,虚线表示乙的图象),则正确的是( )
11、某海产品深加工厂的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排工人装箱,若每小时可以装产品150件,则未装箱的产品数y(件)是时间t(小时)的函数,这个函数的大致图象可能是( )
12、如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省(
)元.
A.3
B.4
C.5
D.6
13、正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=x+4上,则点Bn的坐标为(
)
A.
B.
C.
D.
14、如图,已知A地在B地正南方4千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系,射线AC和射线BD是函数关系的图象,且AC与BD相交于点P,根据图象的信息填空:(1)交点P所表示的实际意义是经过
;(2)当他们行走5小时后,他们之间的距离为
千米.
15、某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的
函数图象如图所示,现有以下4个结论:①快递车从甲地到乙地的速度为100千米/时;②甲、乙两地之间的距离为300km;③甲、乙两地之间的距离为120千米;④图中点B的坐标为(,75);⑤快递车从乙地返回时的速度为90千米/时;⑥点C的实际意义是快递车返回时与货车的相遇点.以上6个结论正确的是
.
16、运动会上甲、乙两人在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:(1)最先到达终点的是______人,比另一人领先______分钟到达.(2)在比赛过程中,甲人______分钟时加速,乙人在______分钟和______分钟时两次加速.(3)甲乙两人到达终点的分别是多少?
?17、某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴16元月租费,然后每通话1分钟,再付话费0.1元;乙种使用者不缴月租费,每通话1分钟,付话费0.3元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.
(1)试分别写出y1、y2与x之间的函数关系式;
(2)在如图所示的坐标系中画出y1、y2的图象;
(3)根据一个月通话时间为120分钟,你认为选用哪种通信业务更优惠.
18、如图,直线l1、l2相交于点P,点P的坐标为(3,4)l1分别与x轴、y轴相交于点A、B,l2与y
轴的交点坐标为C(0,3),结合图像解答下列问题:
(1)求出直线l2表示的一次函数的表达式;
(2)若△PBC的面积为6.9个平方单位,求出直线l1表示的一次函数的表达式;
(3)已知点Q在x轴上,△PQA
与△PDA的面积分别为S△PQA与
S△PDA,且S△PQA=
2S
△PDA,求点Q的坐标.
【中考链接】
19、(2019?宜宾)如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.
乙前4秒行驶的路程为48米
B.
在0到8秒内甲的速度每秒增加4米/秒
C.
两车到第3秒时行驶的路程相等
D.
在4至8秒内甲的速度都大于乙的速度
20、(2019?乌鲁木齐)某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是
A.8.4小时
B.8.6小时
C.8.8小时
D.9小时
21、(2019?大连)甲、乙两人沿同一条直路走步,如果两人分别从这条路上的A,B两处同时出发,都以不变的速度相向而行,图1的甲离开A处后行走的路程y(单位:m)与行走的时间x(单位:min)的函数图象,图2是甲、乙两人之间的距离(单位:m)与甲行走的时间x(单位:min)的函数图象,则ab=
.
参考答案
1、A
2、D
3、B
4、A
5、y=1.6x+2,一次函数,x≥3
6、50,甲
7、(1)2.6,
(2)3.1
10、C
11、D
12、B
13、A
14、4小时后,甲乙两人在距离A地8千米处相遇,1
15、①②④⑤⑥
19、C
20、C
21、
8、声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)的关系如下表:
气温x(℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
①观察上表,气温每升高5℃,音速如何变化?
②求出y与x之间的表达式;
③气温x=25℃时,某人看到闪电6秒后才听到雷声,那么此人与打雷位置的距离有多远?
解:①由表可知,温度每上升5℃,音速增加3m/s;
②设y与x之间的表达式为y=kx+b,
∵根据题意,将x=0,y=331;x=5,y=334,代入y=kx+b得,
b=331,5x+b=334,
解得,x==0.6,b=331,
∴y与x之间的表达式为y=0.6x+331;
③当x=25时,y=0.6×25+331=346(m/s),
距离为:346×6=2076米,
∴此人与打雷位置的距离2076米.
9、某生物小组观察一颗20cm高的玉米苗的生长过程,这颗玉米生长高度y(厘米)与时间x(天)的关系,并画出如图所示的图象(AB是线段,直线BC平行x轴).
(1)从观察时起这颗玉米,多少天以后停止长高?
(2)求直线AB的解析式,并求这颗玉米最高长多少厘米?
解:(1)∵BC∥x轴,
∴从第70天开始这颗玉米的高度不变.
答:这颗玉米从栽种起,70天以后停止长高.
(2)设直线AB的解析式为y=kx+b(k≠0),
∵经过点A(0,20),B(25,75),
∴由题意得,
解得,
∴直线AB的解析式为(0
cm).
答:直线AB的解析式为(0
(1)根据图象可以得到最先到达终点的是乙,
比乙队领先9.5-8.6=0.9分钟;
(2)根据图象可得甲人在第6分钟加速,
乙人在第2分钟和第7分钟时两次加速;
(3)甲人到达终点的速度为:
(1500800)÷(9.56)=200(米/分钟),
乙人到达终点的速度为:
(15001100)÷(8.67)=250(米/分钟).
?17、某电信公司开设了甲、乙两种市内移动通信业务.甲种使用者每月需缴16元月租费,然后每通话1分钟,再付话费0.1元;乙种使用者不缴月租费,每通话1分钟,付话费0.3元.若一个月内通话时间为x分钟,甲、乙两种的费用分别为y1和y2元.
(1)试分别写出y1、y2与x之间的函数关系式;
(2)在如图所示的坐标系中画出y1、y2的图象;
(3)根据一个月通话时间为120分钟,你认为选用哪种通信业务更优惠.
解:(1)由题意得:y1=0.1x+18(x≥0),y2=0.3x(x≥0);
(2)如图所示:
(3)当x=120分钟时,y1=0.1x+18=0.1×120+18=30,
y2=0.3x=0.3×120=36,
∵30<36.
∴当通话时间为120分钟时,选择甲种业务更优惠.
18、如图,直线l1、l2相交于点P,点P的坐标为(3,4)l1分别与x轴、y轴相交于点A、B,l2与y
轴的交点坐标为C(0,3),结合图像解答下列问题:
(1)求出直线l2表示的一次函数的表达式;
(2)若△PBC的面积为6.9个平方单位,求出直线l1表示的一次函数的表达式;
(3)已知点Q在x轴上,△PQA
与△PDA的面积分别为S△PQA与
S△PDA,且S△PQA=
2S
△PDA,求点Q的坐标.
解:(1)设直线l2的解析式为y=kx+b,???则由图象过点(0,3)和(3,4)得,
?b=3,3k+b=4,解得,k=,
?b=3,
∴直线l2表达式y=x3;
(2)∵△PBC的面积为6.9个平方单位,
∴S△PBC=,即=6.9,
解得BC=4.6,
∵点C的坐标为(0,3),
∴OC=3,
OB=BCOC=4.63=1.6,
∴点B的坐标为(0,1.6)
设直线l1的解析式为y=mx+n,?
将点P(3,4)和点B(0,1.6)代入y=mx+n得,
3m+n=4,n=1.6,
解得m=0.8=,
n=1.6=,
直线l1表达式y=x+;
?
(3)令y=x3=0和y=x+=0
解得x=和x=2,
∴点A、D的坐标分别为(2,0)、(,0),
∴AD=AO+OD=2+=,
∵S△PQA=2S
△PDA,且△PQA
与△PDA是同高的三角形,
∴AQ=2AD=2×=,
∴AD=DQ=,
∴=,2+=,
∴点Q的坐标为(,0)或(,0).
第17题图
第17题图
第16题图
第16题图
第7(2)题图
第16题图
第15题图
第13题图
例题2图
第20题图
第3题图
第17题图
第18题图
第12题图
第3题图
第1题图
第9题图
第18题图
第4题图
第21题图1
第21题图2
第19题图
第14题图
第6题图
A
B
C
D
第17题图
第9题图
A
B
C
D
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
