湘教版数学七年级上册单元冲刺卷第2章 代数式(word版,含答案)
文档属性
| 名称 | 湘教版数学七年级上册单元冲刺卷第2章 代数式(word版,含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 643.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 00:00:00 | ||
图片预览


文档简介
第2章
代数式
一、选择题(共15小题;共60分)
1.
下列说法中,不正确的是
A.
的系数是
,次数是
B.
是整式
C.
的项是
,,
D.
是三次二项式
2.
下列不是代数式的是
A.
B.
C.
D.
3.
若
,且
,则
的值等于
A.
B.
C.
D.
4.
已知
,则代数式
的值是
A.
B.
C.
D.
5.
在下列表述中,不能表示代数式“
”的意义的是
A.
的
倍
B.
的
倍
C.
个
相加
D.
个
相乘
6.
若单项式
与
是同类项,则
的值是
A.
B.
C.
D.
7.
若
,则
的值为
A.
B.
C.
D.
8.
已知代数式
与
是同类项,那么
,
的值分别是
A.
B.
C.
D.
9.
有一大捆粗细均匀的钢筋,现要确定其长度.先称出这捆钢筋的总质量为
千克,再从中截取
米长的钢筋,称出它的质量为
千克,那么这捆钢筋的总长度为
A.
米
B.
米
C.
米
D.
米
10.
同时都含有
,,,且系数为
的
次单项式共有
个.
A.
B.
C.
D.
11.
某工厂第一个生产
件产品,第二年比第一年增产了
,则两年共生产产品的件数为
A.
B.
C.
D.
12.
下列各式书写正确的是
A.
B.
C.
D.
13.
把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为
,宽为
)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是
A.
B.
C.
D.
14.
在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①,图②,已知大长方形的长为
,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是
(用
的代数式表示)
A.
B.
C.
D.
15.
下列各式是代数式的是
A.
B.
C.
D.
二、填空题(共8小题;共38分)
16.
若
,
时,代数式
的值为
,则代数式
的值是
?.
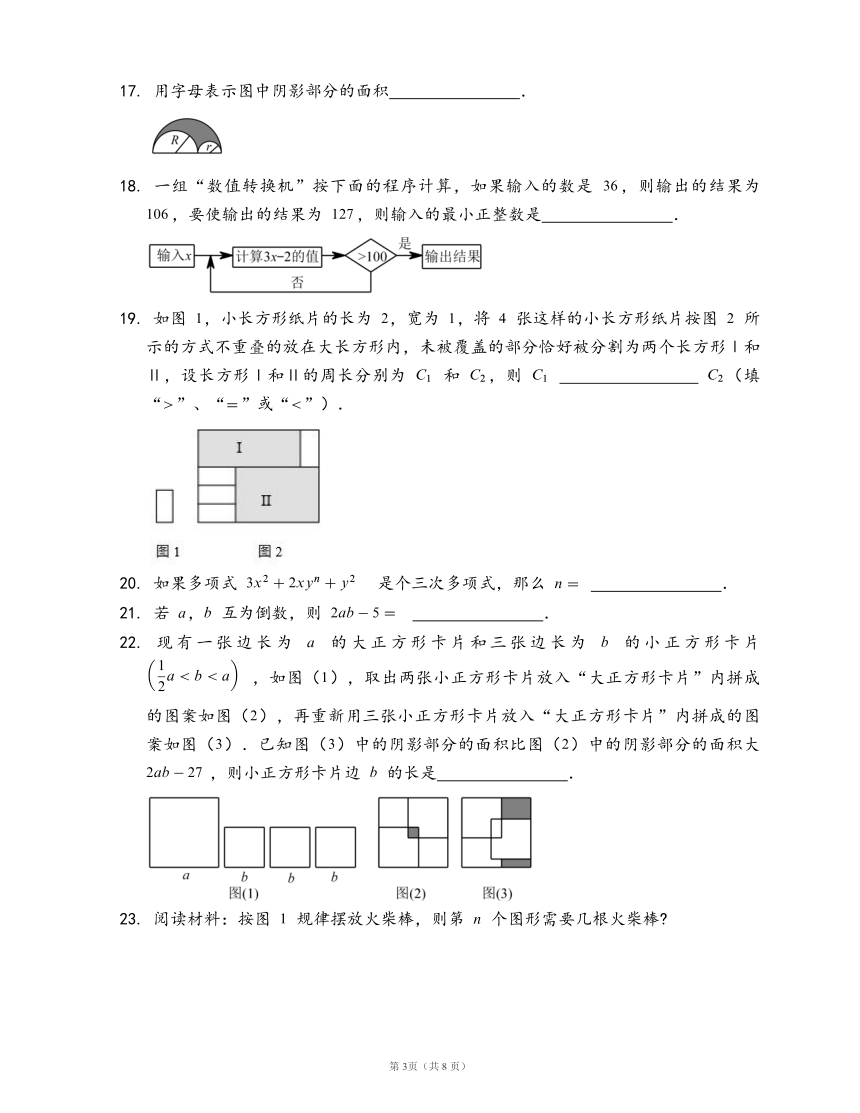
17.
用字母表示图中阴影部分的面积
?.
18.
一组“数值转换机”按下面的程序计算,如果输入的数是
,则输出的结果为
,要使输出的结果为
,则输入的最小正整数是
?.
19.
如图
,小长方形纸片的长为
,宽为
,将
张这样的小长方形纸片按图
所示的方式不重叠的放在大长方形内,未被覆盖的部分恰好被分割为两个长方形Ⅰ和Ⅱ,设长方形Ⅰ和Ⅱ的周长分别为
和
,则
?
(填“”、“”或“”).
20.
如果多项式
是个三次多项式,那么
?.
21.
若
,
互为倒数,则
?.
22.
现有一张边长为
的大正方形卡片和三张边长为
的小正方形卡片
,如图(),取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图(),再重新用三张小正方形卡片放入“大正方形卡片”内拼成的图案如图().已知图()中的阴影部分的面积比图()中的阴影部分的面积大
,则小正方形卡片边
的长是
?.
23.
阅读材料:按图
规律摆放火柴棒,则第
个图形需要几根火柴棒?
解法
:从数列出发.
由第
个图形需要
根火柴棒,第
个图形需要
根火柴棒,第
个图形需要
根火柴棒,,我们得到一组数列:
,,,(自己画出第
个图形可得到),
将原数列中的每一个数据同时减去
,得到新的数列:
,,,,
很容易发现是
的倍数,即第
个数是
.
则原数列第
个数就是
.
解法
:从图形摆放的规律出发.
可以看成是以“”这种形式堆积上去的图形,则
第一个图形:
个“”
根火柴棒,即
;
第二个图形:
个“”
根火柴棒,即
;
第三个图形:
个“”
根火柴棒,即
;
第
个图形:
个“”
根火柴棒,即
.
现在,让我们通过上述阅读材料来完成下面的题目:
用同样的火柴棒按图
规律摆图,则摆第
个图形需要
?根火柴棒.
三、解答题(共4小题;共52分)
24.
小丽和小明设计了一个电脑程序,在电脑执行该程序时,第一步会将输入的数值乘以
,第二步将乘积的结果减去
,第三步将所得差取绝对值后输出.
(1)如果输入的数是
,那么输出的结果用
的代数式表示是什么?
(2)如果输入的数是
,那么输出的结果是什么?(写出代入计算过程)
25.
求
的值,其中
.
26.
已知
与
是同类项、
的系数为
,
的次数是
:先分别求出
,,,然后计算
的值.
27.
小明设计了一个电脑程序,在电脑执行该程序时,第一步会将输入的数值进行平方,第二步将平方的结果减去
,第三步将所得差取倒数后输出.
(1)如果输入的数是
,那么输出的结果用
的代数式来表示是什么?
(2)如果输入的数是
,那么输出的结果是什么?
答案
第一部分
1.
D
2.
B
3.
C
4.
B
5.
D
6.
D
【解析】根据题意得:
解得:
,
则
.
7.
D
【解析】,
8.
A
【解析】由题意,得
解得
9.
C
10.
C
【解析】设
为所求单项式,,,
都是正整数,且由
可知:
当
时,共有
个;
当
时,有
个;
当
时,有
个;
当
时,有
个;
当
时,有
个,
所以共有
个.
11.
D
12.
D
13.
B
14.
C
【解析】设图③中小长方形的长为
,宽为
,大长方形的宽为
.
根据题意得:,,即
.
图①中阴影部分的周长为
,
图②中阴影部分的周长
,
则图①阴影部分周长与图②阴影部分周长之差为
.
15.
C
第二部分
16.
17.
18.
19.
20.
【解析】该多项式共有三项:,,,
其中
,
是二次项,
是三次项,
根据单项式的次数的定义,,解得
.
21.
22.
23.
【解析】提示:
解法一(图形排布规律).
解法二(从数列出发).
故原数列为
.
第三部分
24.
(1)
.
??????(2)
.
25.
当
时,
26.
根据题意得
,,,
解得
,,,
则
27.
(1)
.
??????(2)
.
第1页(共8
页)
代数式
一、选择题(共15小题;共60分)
1.
下列说法中,不正确的是
A.
的系数是
,次数是
B.
是整式
C.
的项是
,,
D.
是三次二项式
2.
下列不是代数式的是
A.
B.
C.
D.
3.
若
,且
,则
的值等于
A.
B.
C.
D.
4.
已知
,则代数式
的值是
A.
B.
C.
D.
5.
在下列表述中,不能表示代数式“
”的意义的是
A.
的
倍
B.
的
倍
C.
个
相加
D.
个
相乘
6.
若单项式
与
是同类项,则
的值是
A.
B.
C.
D.
7.
若
,则
的值为
A.
B.
C.
D.
8.
已知代数式
与
是同类项,那么
,
的值分别是
A.
B.
C.
D.
9.
有一大捆粗细均匀的钢筋,现要确定其长度.先称出这捆钢筋的总质量为
千克,再从中截取
米长的钢筋,称出它的质量为
千克,那么这捆钢筋的总长度为
A.
米
B.
米
C.
米
D.
米
10.
同时都含有
,,,且系数为
的
次单项式共有
个.
A.
B.
C.
D.
11.
某工厂第一个生产
件产品,第二年比第一年增产了
,则两年共生产产品的件数为
A.
B.
C.
D.
12.
下列各式书写正确的是
A.
B.
C.
D.
13.
把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为
,宽为
)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是
A.
B.
C.
D.
14.
在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①,图②,已知大长方形的长为
,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是
(用
的代数式表示)
A.
B.
C.
D.
15.
下列各式是代数式的是
A.
B.
C.
D.
二、填空题(共8小题;共38分)
16.
若
,
时,代数式
的值为
,则代数式
的值是
?.
17.
用字母表示图中阴影部分的面积
?.
18.
一组“数值转换机”按下面的程序计算,如果输入的数是
,则输出的结果为
,要使输出的结果为
,则输入的最小正整数是
?.
19.
如图
,小长方形纸片的长为
,宽为
,将
张这样的小长方形纸片按图
所示的方式不重叠的放在大长方形内,未被覆盖的部分恰好被分割为两个长方形Ⅰ和Ⅱ,设长方形Ⅰ和Ⅱ的周长分别为
和
,则
?
(填“”、“”或“”).
20.
如果多项式
是个三次多项式,那么
?.
21.
若
,
互为倒数,则
?.
22.
现有一张边长为
的大正方形卡片和三张边长为
的小正方形卡片
,如图(),取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图(),再重新用三张小正方形卡片放入“大正方形卡片”内拼成的图案如图().已知图()中的阴影部分的面积比图()中的阴影部分的面积大
,则小正方形卡片边
的长是
?.
23.
阅读材料:按图
规律摆放火柴棒,则第
个图形需要几根火柴棒?
解法
:从数列出发.
由第
个图形需要
根火柴棒,第
个图形需要
根火柴棒,第
个图形需要
根火柴棒,,我们得到一组数列:
,,,(自己画出第
个图形可得到),
将原数列中的每一个数据同时减去
,得到新的数列:
,,,,
很容易发现是
的倍数,即第
个数是
.
则原数列第
个数就是
.
解法
:从图形摆放的规律出发.
可以看成是以“”这种形式堆积上去的图形,则
第一个图形:
个“”
根火柴棒,即
;
第二个图形:
个“”
根火柴棒,即
;
第三个图形:
个“”
根火柴棒,即
;
第
个图形:
个“”
根火柴棒,即
.
现在,让我们通过上述阅读材料来完成下面的题目:
用同样的火柴棒按图
规律摆图,则摆第
个图形需要
?根火柴棒.
三、解答题(共4小题;共52分)
24.
小丽和小明设计了一个电脑程序,在电脑执行该程序时,第一步会将输入的数值乘以
,第二步将乘积的结果减去
,第三步将所得差取绝对值后输出.
(1)如果输入的数是
,那么输出的结果用
的代数式表示是什么?
(2)如果输入的数是
,那么输出的结果是什么?(写出代入计算过程)
25.
求
的值,其中
.
26.
已知
与
是同类项、
的系数为
,
的次数是
:先分别求出
,,,然后计算
的值.
27.
小明设计了一个电脑程序,在电脑执行该程序时,第一步会将输入的数值进行平方,第二步将平方的结果减去
,第三步将所得差取倒数后输出.
(1)如果输入的数是
,那么输出的结果用
的代数式来表示是什么?
(2)如果输入的数是
,那么输出的结果是什么?
答案
第一部分
1.
D
2.
B
3.
C
4.
B
5.
D
6.
D
【解析】根据题意得:
解得:
,
则
.
7.
D
【解析】,
8.
A
【解析】由题意,得
解得
9.
C
10.
C
【解析】设
为所求单项式,,,
都是正整数,且由
可知:
当
时,共有
个;
当
时,有
个;
当
时,有
个;
当
时,有
个;
当
时,有
个,
所以共有
个.
11.
D
12.
D
13.
B
14.
C
【解析】设图③中小长方形的长为
,宽为
,大长方形的宽为
.
根据题意得:,,即
.
图①中阴影部分的周长为
,
图②中阴影部分的周长
,
则图①阴影部分周长与图②阴影部分周长之差为
.
15.
C
第二部分
16.
17.
18.
19.
20.
【解析】该多项式共有三项:,,,
其中
,
是二次项,
是三次项,
根据单项式的次数的定义,,解得
.
21.
22.
23.
【解析】提示:
解法一(图形排布规律).
解法二(从数列出发).
故原数列为
.
第三部分
24.
(1)
.
??????(2)
.
25.
当
时,
26.
根据题意得
,,,
解得
,,,
则
27.
(1)
.
??????(2)
.
第1页(共8
页)
同课章节目录
