第13章 全等三角形综合能力提升卷(附解析)
文档属性
| 名称 | 第13章 全等三角形综合能力提升卷(附解析) |  | |
| 格式 | zip | ||
| 文件大小 | 344.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 22:41:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第13章
全等三角形
综合能力提升卷
一、选择题(共9小题)
1.如图,5个边长相等的正六边形,A、B、C、D、E,请仔细观察A、B、C、D四个答案,其中与右方图案完全相同的是( )
A.
B.
C.
D.
2.尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
A.SAS
B.ASA
C.AAS
D.SSS
3.如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( )
A.∠BAD=∠CAE
B.△ABD≌△ACE
C.AB=BC
D.BD=CE
4.如图,AB∥CD,AD∥BC,AC、BD相交于点O,过O点作一直线交AD于E,交BC于F,则图中全等三角形共有( )
A.4对
B.5对
C.6对
D.7对
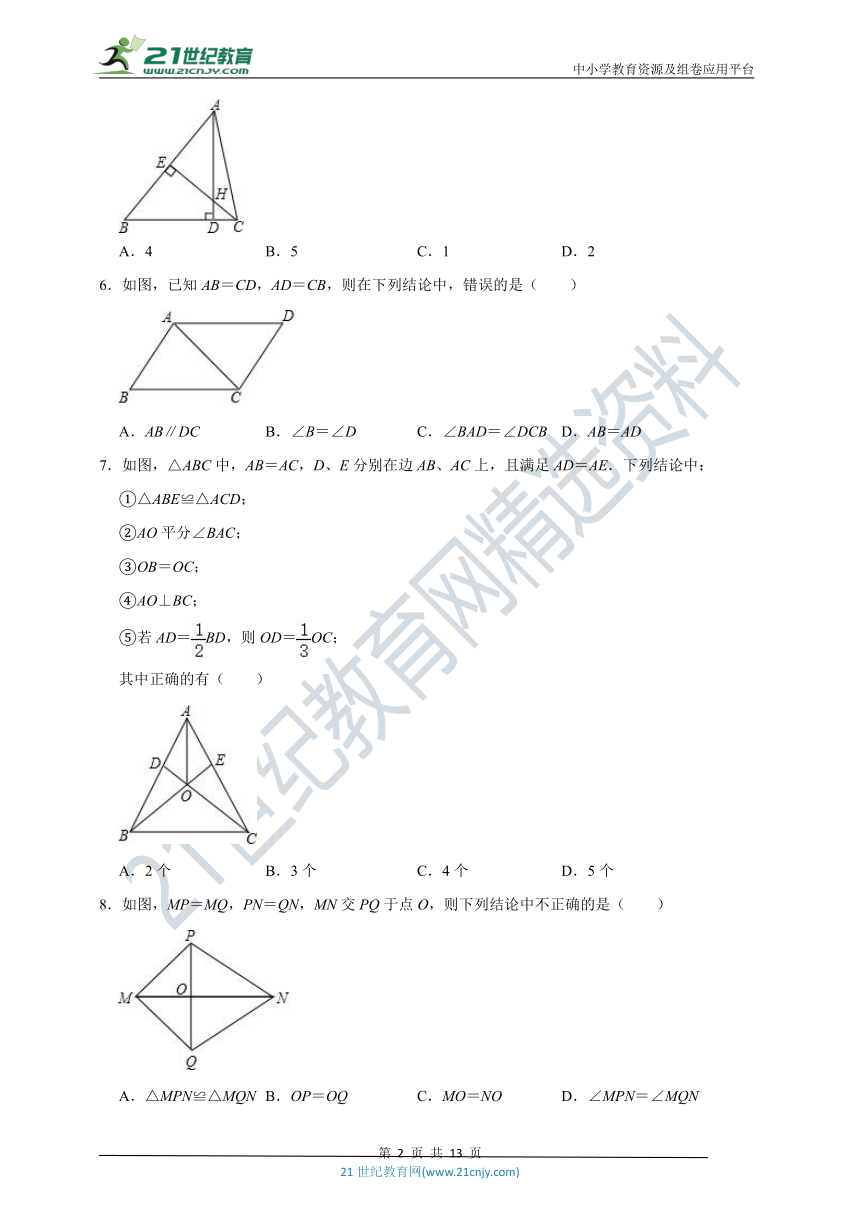
5.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )
A.4
B.5
C.1
D.2
6.如图,已知AB=CD,AD=CB,则在下列结论中,错误的是( )
A.AB∥DC
B.∠B=∠D
C.∠BAD=∠DCB
D.AB=AD
7.如图,△ABC中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:
①△ABE≌△ACD;
②AO平分∠BAC;
③OB=OC;
④AO⊥BC;
⑤若AD=BD,则OD=OC;
其中正确的有( )
A.2个
B.3个
C.4个
D.5个
8.如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论中不正确的是( )
A.△MPN≌△MQN
B.OP=OQ
C.MO=NO
D.∠MPN=∠MQN
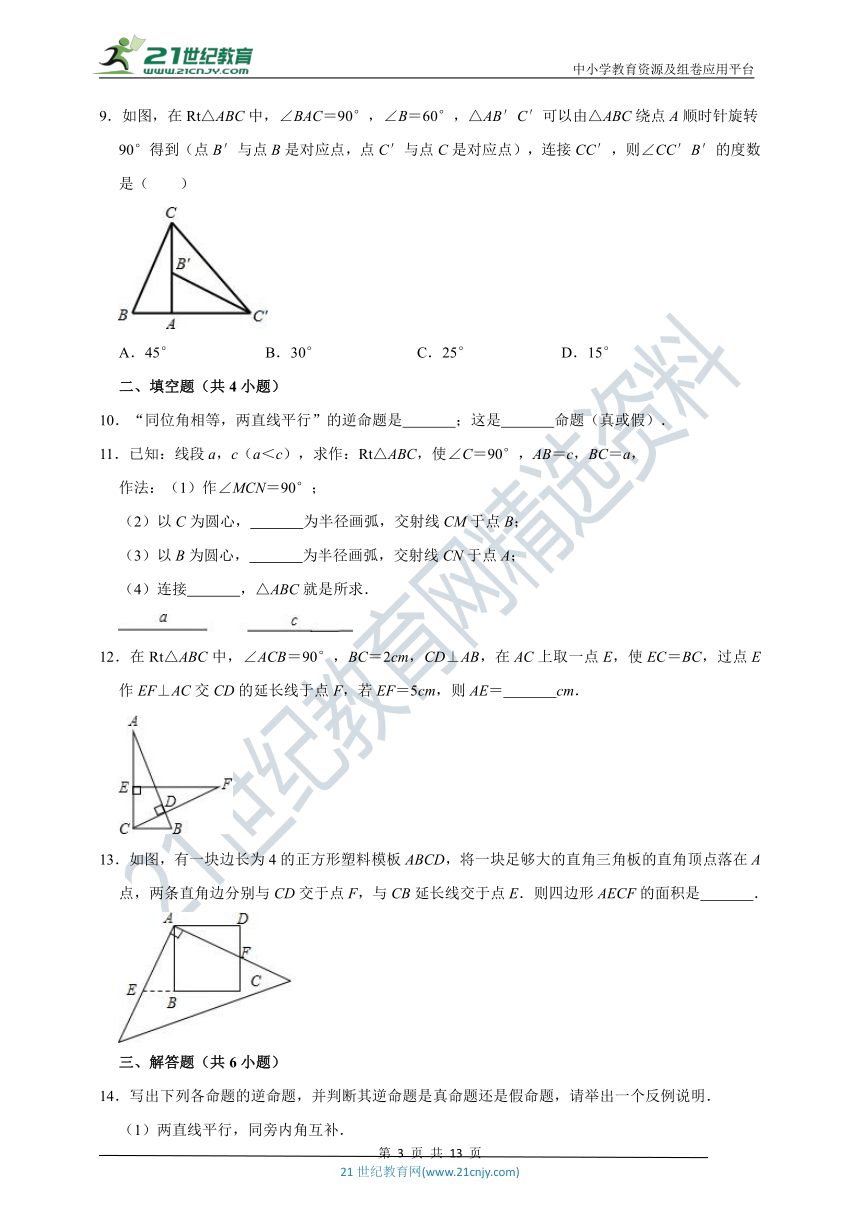
9.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( )
A.45°
B.30°
C.25°
D.15°
二、填空题(共4小题)
10.“同位角相等,两直线平行”的逆命题是
;这是
命题(真或假).
11.已知:线段a,c(a<c),求作:Rt△ABC,使∠C=90°,AB=c,BC=a,
作法:(1)作∠MCN=90°;
(2)以C为圆心,
为半径画弧,交射线CM于点B;
(3)以B为圆心,
为半径画弧,交射线CN于点A;
(4)连接
,△ABC就是所求.
12.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=
cm.
13.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是
.
三、解答题(共6小题)
14.写出下列各命题的逆命题,并判断其逆命题是真命题还是假命题,请举出一个反例说明.
(1)两直线平行,同旁内角互补.
(2)垂直于同一条直线的两直线平行.
(3)相等的角是内错角.
(4)等底等高的三角形面积相等.
15.如图,已知线段a及∠O,只用直尺和圆规,求作△ABC,使BC=a,∠B=∠O,∠C=2∠B(在指定作图区域作图,保留作图痕迹,不写作法)
16.如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC.当O沿AD滑动时,雨伞开闭.雨伞开闭过程中,∠BAD与∠CAD有何关系?请说明理由.
17.如图,已知△ABC≌△ADE,AB与ED交于点M,BC与ED,AD分别交于点F,N.请写出图中两对全等三角形(△ABC≌△ADE除外),并选择其中的一对加以证明.
18.把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE、AD,AD的延长线交BE于点F.
(1)求证:AD=BE;
(2)判断AF和BE的位置关系并说明理由.
19.小明站在池塘边的A点处,池塘的对面(小明的正北方向)B处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了10步到达电线杆C旁,接着再往前走了10步,到达D处,然后他改向正南方向继续行走,当小明看到电线杆C、小树B与自己现处的位置E在一条直线上时,他共走了45步.
(1)根据题意,画出示意图;
(2)如果小明一步大约40厘米,估算出小明在点A处时小树与他的距离,并说明理由.
试题解析
1.解:观察图形可知,
只有选项C中的图形旋转后与图中的正六边形完全相同.
故选:C.
2.解:∵以O为圆心,任意长为半径画弧交OA,OB于C,D,即OC=OD;
以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,即CP=DP;
在△OCP和△ODP中,
,
∴△OCP≌△ODP(SSS).
故选:D.
3.证明:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,故A正确,
在△BAD和△ACE中,
,
∴△BAD≌△CAE,故B正确,
∴BD=EC,故D正确,
∴C错误,
故选:C.
4.解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
由平行四边形的中心对称性,
全等三角形有:△AOB≌△COD,△AOD≌△COB,△AOE≌△COF,△DOE≌△BOF,△ABD≌△CDB,△ABC≌△CDA共6对.
故选:C.
5.解:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠AEH=90°,
∵∠AHE=∠CHD,
∴∠BAD=∠BCE,
∵在△HEA和△BEC中,
,
∴△HEA≌△BEC(AAS),
∴AE=EC=4,
则CH=EC﹣EH=AE﹣EH=4﹣3=1.
故选:C.
6.解:∵在△ABC和△CDA中
∴△ABC≌△CDA,
∴∠B=∠D,AB=DC,∠BAC=∠DCA,∠ACB=∠CAD,
∴AB∥DC,∠BAC+∠CAD=∠ACD+∠ACB,
∴∠BAD=∠DCB,
即只有选项D符合题意,选项A、B、C都不符合题意,
故选:D.
7.解:在△ABE与△ACD中,,
∴△ABE≌△ACD,故①正确;
∴∠AEB=∠ADC,
∴∠BDO=∠BEC,
∵AB=AC,AD=AE,
∴BD=CE,
在△BOD与△COE中,,
∴△BOD≌△COE,
∴OD=OE,BO=OC,故③正确;
在△AOD与△AOE中,,
∴△AOD≌△AOE,
∴∠DAO=∠EAO,∠AOD=∠AOF,
∴AO平分∠BAC,故②正确;
∵AB=AC,AO平分∠BAC,
∴AO⊥BC,故④正确;
过D作DF∥AO交BO于F,
∵AD=BD,
∴OF=OB,
∵DF∥AO,
∴∠ODF=∠AOD,∠OFD=∠AOE,
∴∠ODF=∠OFD,
∴OD=OF,
∵OB=OC,
∴OD=OC;故⑤正确;
故选:D.
8.解:∵MP=MQ,PN=QN,MN=MN,
∴△MPN≌△MQN
故A正确;
∵MN垂直平分PQ
∴OP=OQ
故B正确;
∴∠MPN=∠MQN
故D正确.
∴只有C是错误的.
故选:C.
9.解:由旋转的性质可知,AC=AC′,
又∠CAC′=90°,可知△CAC′为等腰直角三角形,
所以,∠CC′A=45°.
∵∠CC′B′+∠ACC′=∠AB′C′=∠B=60°,
∴∠CC′B′=15°.
故选:D.
10.解:“同位角相等,两直线平行”的逆命题是“两直线平行,同位角相等”;这是真命题.
故答案为两直线平行,同位角相等,真.
11.解:作法:(1)作∠MCN=90°;
(2)以C为圆心,a为半径画弧,交射线CM于点B;
(3)以B为圆心,c为半径画弧,交射线CN于点A;
(4)连接
AB,△ABC就是所求.
如图所示:
故答案为:a,c,AB.
12.解:∵∠ACB=90°,
∴∠ECF+∠BCD=90°,
∵CD⊥AB,
∴∠BCD+∠B=90°,
∴∠ECF=∠B(等角的余角相等),
在△FCE和△ABC中,,
∴△ABC≌△FEC(ASA),
∴AC=EF,
∵AE=AC﹣CE,BC=2cm,EF=5cm,
∴AE=5﹣2=3cm.
故答案为:3.
13.解:∵四边形ABCD为正方形,
∴∠D=∠ABC=90°,AD=AB,
∴∠ABE=∠D=90°,
∵∠EAF=90°,
∴∠DAF+∠BAF=90°,∠BAE+∠BAF=90°,
∴∠DAF=∠BAE,
在△AEB和△AFD中,
∵,
∴△AEB≌△AFD(ASA),
∴S△AEB=S△AFD,
∴它们都加上四边形ABCF的面积,
可得到四边形AECF的面积=正方形的面积=16.
故答案为:16.
14.解:(1)同旁内角互补,两直线平行,真命题;
(2)如果两条直线平行,那么这两条直线垂直于同一条直线(在同一平面内),真命题;
(3)内错角相等,假命题;例如:∠1与∠2是内错角,但不相等;
(4)面积相等的三角形等底等高,是假命题.例如:底边是2,高是4的三角形与底边是4,高是2的三角形.
15.解:如图所示:
.
16.解:∠BAD=∠CAD,
理由:∵AB=AC,AE=AB,AF=AC,
∴AE=AF,
在△AEO和△AFO中,
,
∴△AEO≌△AFO(SSS),
∴∠BAD=∠CAD.
17.解:△AEM≌△ACN,△BMF≌△DNF,△ABN≌△ADM.
选择△AEM≌△ACN,
理由如下:
∵△ADE≌△ABC,
∴AE=AC,∠E=∠C,∠EAD=∠CAB,
∴∠EAM=∠CAN,
∵在△AEM和△ACN中,
∴△AEM≌△ACN(ASA).
18.(1)证明:∵△CDE,△ACB都是等腰直角三角形,
∴CE=CD,CB=CA,∠ACD=∠BCE=90°,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)解:结论:AF⊥BE.
理由:∵△ACD≌△BCE,
∴∠CAD=CBE,
∵∠CDA=∠BDF,
∴∠BFD=∠ACD=90°,
∴AF⊥BE.
19.解:(1)①连接AC并延长至D,使AC=CD;
②过D作DE⊥AD交直线BC于点E;
(2)∵AC=CD=10步,AC+CD+DE=45步,一步大约40厘米,
∴AC=CD=10×40=400厘米,
DE=45﹣20=25步=25×40=1000厘米,
∵AB⊥AD,DE⊥AD,
∴在△ABC与△DEC中,
∠BAC=∠CDE,AC=DC,∠ACB=∠DCE,
∴△ABC≌△DEC,
∴AB=DE=1000厘米=10米.
故答案为:10米.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第13章
全等三角形
综合能力提升卷
一、选择题(共9小题)
1.如图,5个边长相等的正六边形,A、B、C、D、E,请仔细观察A、B、C、D四个答案,其中与右方图案完全相同的是( )
A.
B.
C.
D.
2.尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
A.SAS
B.ASA
C.AAS
D.SSS
3.如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是( )
A.∠BAD=∠CAE
B.△ABD≌△ACE
C.AB=BC
D.BD=CE
4.如图,AB∥CD,AD∥BC,AC、BD相交于点O,过O点作一直线交AD于E,交BC于F,则图中全等三角形共有( )
A.4对
B.5对
C.6对
D.7对
5.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是( )
A.4
B.5
C.1
D.2
6.如图,已知AB=CD,AD=CB,则在下列结论中,错误的是( )
A.AB∥DC
B.∠B=∠D
C.∠BAD=∠DCB
D.AB=AD
7.如图,△ABC中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:
①△ABE≌△ACD;
②AO平分∠BAC;
③OB=OC;
④AO⊥BC;
⑤若AD=BD,则OD=OC;
其中正确的有( )
A.2个
B.3个
C.4个
D.5个
8.如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论中不正确的是( )
A.△MPN≌△MQN
B.OP=OQ
C.MO=NO
D.∠MPN=∠MQN
9.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( )
A.45°
B.30°
C.25°
D.15°
二、填空题(共4小题)
10.“同位角相等,两直线平行”的逆命题是
;这是
命题(真或假).
11.已知:线段a,c(a<c),求作:Rt△ABC,使∠C=90°,AB=c,BC=a,
作法:(1)作∠MCN=90°;
(2)以C为圆心,
为半径画弧,交射线CM于点B;
(3)以B为圆心,
为半径画弧,交射线CN于点A;
(4)连接
,△ABC就是所求.
12.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=
cm.
13.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是
.
三、解答题(共6小题)
14.写出下列各命题的逆命题,并判断其逆命题是真命题还是假命题,请举出一个反例说明.
(1)两直线平行,同旁内角互补.
(2)垂直于同一条直线的两直线平行.
(3)相等的角是内错角.
(4)等底等高的三角形面积相等.
15.如图,已知线段a及∠O,只用直尺和圆规,求作△ABC,使BC=a,∠B=∠O,∠C=2∠B(在指定作图区域作图,保留作图痕迹,不写作法)
16.如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC.当O沿AD滑动时,雨伞开闭.雨伞开闭过程中,∠BAD与∠CAD有何关系?请说明理由.
17.如图,已知△ABC≌△ADE,AB与ED交于点M,BC与ED,AD分别交于点F,N.请写出图中两对全等三角形(△ABC≌△ADE除外),并选择其中的一对加以证明.
18.把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE、AD,AD的延长线交BE于点F.
(1)求证:AD=BE;
(2)判断AF和BE的位置关系并说明理由.
19.小明站在池塘边的A点处,池塘的对面(小明的正北方向)B处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了10步到达电线杆C旁,接着再往前走了10步,到达D处,然后他改向正南方向继续行走,当小明看到电线杆C、小树B与自己现处的位置E在一条直线上时,他共走了45步.
(1)根据题意,画出示意图;
(2)如果小明一步大约40厘米,估算出小明在点A处时小树与他的距离,并说明理由.
试题解析
1.解:观察图形可知,
只有选项C中的图形旋转后与图中的正六边形完全相同.
故选:C.
2.解:∵以O为圆心,任意长为半径画弧交OA,OB于C,D,即OC=OD;
以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,即CP=DP;
在△OCP和△ODP中,
,
∴△OCP≌△ODP(SSS).
故选:D.
3.证明:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,故A正确,
在△BAD和△ACE中,
,
∴△BAD≌△CAE,故B正确,
∴BD=EC,故D正确,
∴C错误,
故选:C.
4.解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
由平行四边形的中心对称性,
全等三角形有:△AOB≌△COD,△AOD≌△COB,△AOE≌△COF,△DOE≌△BOF,△ABD≌△CDB,△ABC≌△CDA共6对.
故选:C.
5.解:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠AEH=90°,
∵∠AHE=∠CHD,
∴∠BAD=∠BCE,
∵在△HEA和△BEC中,
,
∴△HEA≌△BEC(AAS),
∴AE=EC=4,
则CH=EC﹣EH=AE﹣EH=4﹣3=1.
故选:C.
6.解:∵在△ABC和△CDA中
∴△ABC≌△CDA,
∴∠B=∠D,AB=DC,∠BAC=∠DCA,∠ACB=∠CAD,
∴AB∥DC,∠BAC+∠CAD=∠ACD+∠ACB,
∴∠BAD=∠DCB,
即只有选项D符合题意,选项A、B、C都不符合题意,
故选:D.
7.解:在△ABE与△ACD中,,
∴△ABE≌△ACD,故①正确;
∴∠AEB=∠ADC,
∴∠BDO=∠BEC,
∵AB=AC,AD=AE,
∴BD=CE,
在△BOD与△COE中,,
∴△BOD≌△COE,
∴OD=OE,BO=OC,故③正确;
在△AOD与△AOE中,,
∴△AOD≌△AOE,
∴∠DAO=∠EAO,∠AOD=∠AOF,
∴AO平分∠BAC,故②正确;
∵AB=AC,AO平分∠BAC,
∴AO⊥BC,故④正确;
过D作DF∥AO交BO于F,
∵AD=BD,
∴OF=OB,
∵DF∥AO,
∴∠ODF=∠AOD,∠OFD=∠AOE,
∴∠ODF=∠OFD,
∴OD=OF,
∵OB=OC,
∴OD=OC;故⑤正确;
故选:D.
8.解:∵MP=MQ,PN=QN,MN=MN,
∴△MPN≌△MQN
故A正确;
∵MN垂直平分PQ
∴OP=OQ
故B正确;
∴∠MPN=∠MQN
故D正确.
∴只有C是错误的.
故选:C.
9.解:由旋转的性质可知,AC=AC′,
又∠CAC′=90°,可知△CAC′为等腰直角三角形,
所以,∠CC′A=45°.
∵∠CC′B′+∠ACC′=∠AB′C′=∠B=60°,
∴∠CC′B′=15°.
故选:D.
10.解:“同位角相等,两直线平行”的逆命题是“两直线平行,同位角相等”;这是真命题.
故答案为两直线平行,同位角相等,真.
11.解:作法:(1)作∠MCN=90°;
(2)以C为圆心,a为半径画弧,交射线CM于点B;
(3)以B为圆心,c为半径画弧,交射线CN于点A;
(4)连接
AB,△ABC就是所求.
如图所示:
故答案为:a,c,AB.
12.解:∵∠ACB=90°,
∴∠ECF+∠BCD=90°,
∵CD⊥AB,
∴∠BCD+∠B=90°,
∴∠ECF=∠B(等角的余角相等),
在△FCE和△ABC中,,
∴△ABC≌△FEC(ASA),
∴AC=EF,
∵AE=AC﹣CE,BC=2cm,EF=5cm,
∴AE=5﹣2=3cm.
故答案为:3.
13.解:∵四边形ABCD为正方形,
∴∠D=∠ABC=90°,AD=AB,
∴∠ABE=∠D=90°,
∵∠EAF=90°,
∴∠DAF+∠BAF=90°,∠BAE+∠BAF=90°,
∴∠DAF=∠BAE,
在△AEB和△AFD中,
∵,
∴△AEB≌△AFD(ASA),
∴S△AEB=S△AFD,
∴它们都加上四边形ABCF的面积,
可得到四边形AECF的面积=正方形的面积=16.
故答案为:16.
14.解:(1)同旁内角互补,两直线平行,真命题;
(2)如果两条直线平行,那么这两条直线垂直于同一条直线(在同一平面内),真命题;
(3)内错角相等,假命题;例如:∠1与∠2是内错角,但不相等;
(4)面积相等的三角形等底等高,是假命题.例如:底边是2,高是4的三角形与底边是4,高是2的三角形.
15.解:如图所示:
.
16.解:∠BAD=∠CAD,
理由:∵AB=AC,AE=AB,AF=AC,
∴AE=AF,
在△AEO和△AFO中,
,
∴△AEO≌△AFO(SSS),
∴∠BAD=∠CAD.
17.解:△AEM≌△ACN,△BMF≌△DNF,△ABN≌△ADM.
选择△AEM≌△ACN,
理由如下:
∵△ADE≌△ABC,
∴AE=AC,∠E=∠C,∠EAD=∠CAB,
∴∠EAM=∠CAN,
∵在△AEM和△ACN中,
∴△AEM≌△ACN(ASA).
18.(1)证明:∵△CDE,△ACB都是等腰直角三角形,
∴CE=CD,CB=CA,∠ACD=∠BCE=90°,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)解:结论:AF⊥BE.
理由:∵△ACD≌△BCE,
∴∠CAD=CBE,
∵∠CDA=∠BDF,
∴∠BFD=∠ACD=90°,
∴AF⊥BE.
19.解:(1)①连接AC并延长至D,使AC=CD;
②过D作DE⊥AD交直线BC于点E;
(2)∵AC=CD=10步,AC+CD+DE=45步,一步大约40厘米,
∴AC=CD=10×40=400厘米,
DE=45﹣20=25步=25×40=1000厘米,
∵AB⊥AD,DE⊥AD,
∴在△ABC与△DEC中,
∠BAC=∠CDE,AC=DC,∠ACB=∠DCE,
∴△ABC≌△DEC,
∴AB=DE=1000厘米=10米.
故答案为:10米.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
