第17章 特殊三角形综合能力提升卷(附解析)
文档属性
| 名称 | 第17章 特殊三角形综合能力提升卷(附解析) |  | |
| 格式 | zip | ||
| 文件大小 | 333.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-22 22:53:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第17章
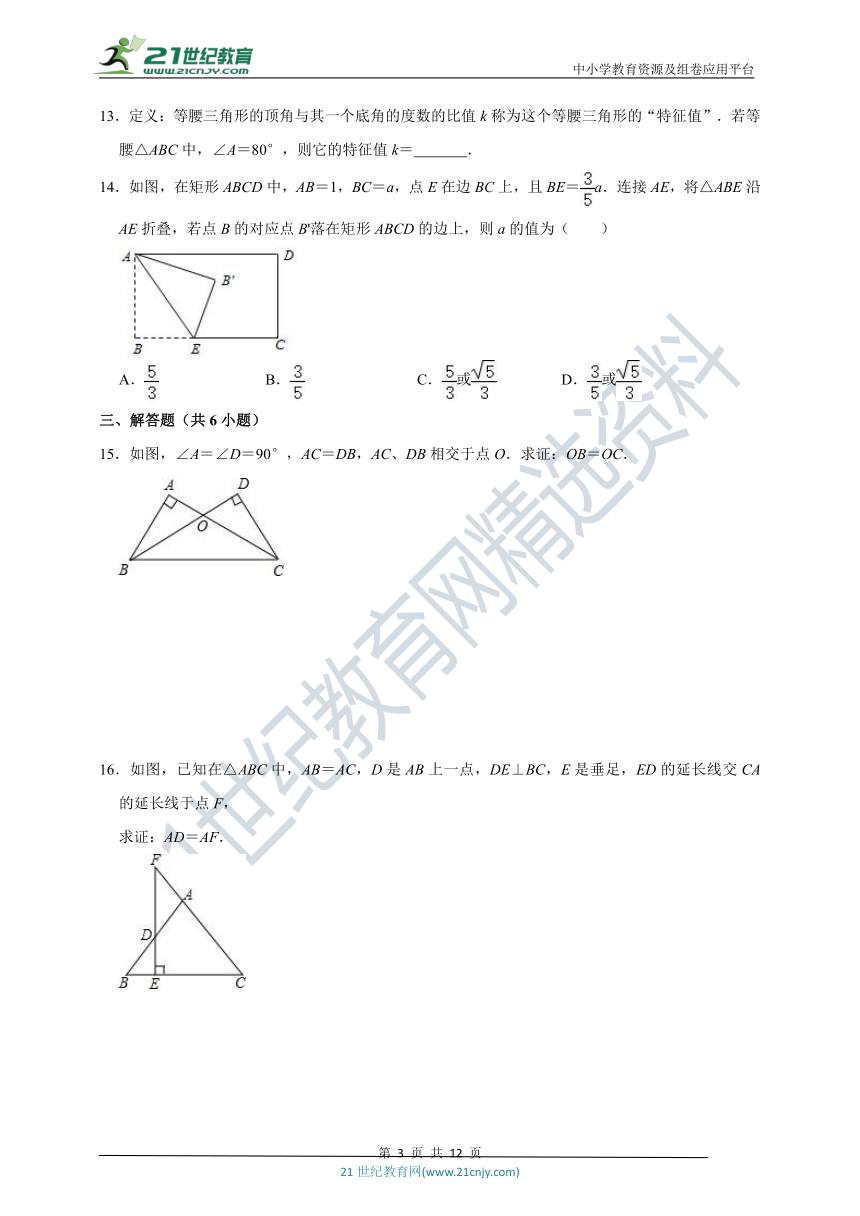
特殊三角形
综合能力提升卷
一、选择题(共10小题)
1.下列条件中,不能判断△ABC为直角三角形的是( )
A.a2=1,b2=2,c2=3
B.a:b:c=3:4:5
C.∠A+∠B=∠C
D.∠A:∠B:∠C=3:4:5
2.将等腰直角三角形纸片和矩形纸片按如图方式叠放在起,若∠1=30°,则∠2的度数为( )
A.10°
B.15°
C.20°
D.30°
3.将一个有45°角的三角尺的直角顶点C放在一张宽为3cm的纸带边沿上,另一个顶点A在纸带的另一边沿上,测得三角尺的一边AC与纸带的一边所在的直线成30°角,如图,则三角尺的最长边的长为( )
A.6
B.3
C.4
D.6
4.下列语句中不正确的是( )
A.斜边和一锐角对应相等的两个直角三角形全等
B.有两边对应相等的两个直角三角形全等
C.有两个锐角相等的两个直角三角形全等
D.有一直角边和一锐角对应相等的两个直角三角形全等
5.如图所示,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前( )米.
A.15
B.20
C.3
D.24
6.若一个直角三角形的三边长为6,8,x,则x的值是( )
A.10
B.2
C.10或2
D.7
7.如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交BC于点D,连接AD,则∠CAD的度数是( )
A.20°
B.30°
C.45°
D.60°
8.等腰三角形一腰上的高与另一腰的夹角为20°,则顶角的度数为( )
A.70°
B.55°
C.110°
D.70°或110°
9.如图,在等边△ABC中,AB=8,E是BA延长线上一点,且EA=4,D是BC上一点,且ED=EC,则BD的长为( )
A.3
B.4
C.5
D.6
10.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=3,BC=8,则△EFM的周长是( )
A.7
B.10
C.11
D.14
二、填空题(共4小题)
11.请举反例说明命题:“两个锐角的和是锐角”是假命题.反例如:
.
12.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是
.
13.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k=
.
14.如图,在矩形ABCD中,AB=1,BC=a,点E在边BC上,且BE=a.连接AE,将△ABE沿AE折叠,若点B的对应点B'落在矩形ABCD的边上,则a的值为( )
A.
B.
C.或
D.或
三、解答题(共6小题)
15.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
16.如图,已知在△ABC中,AB=AC,D是AB上一点,DE⊥BC,E是垂足,ED的延长线交CA的延长线于点F,
求证:AD=AF.
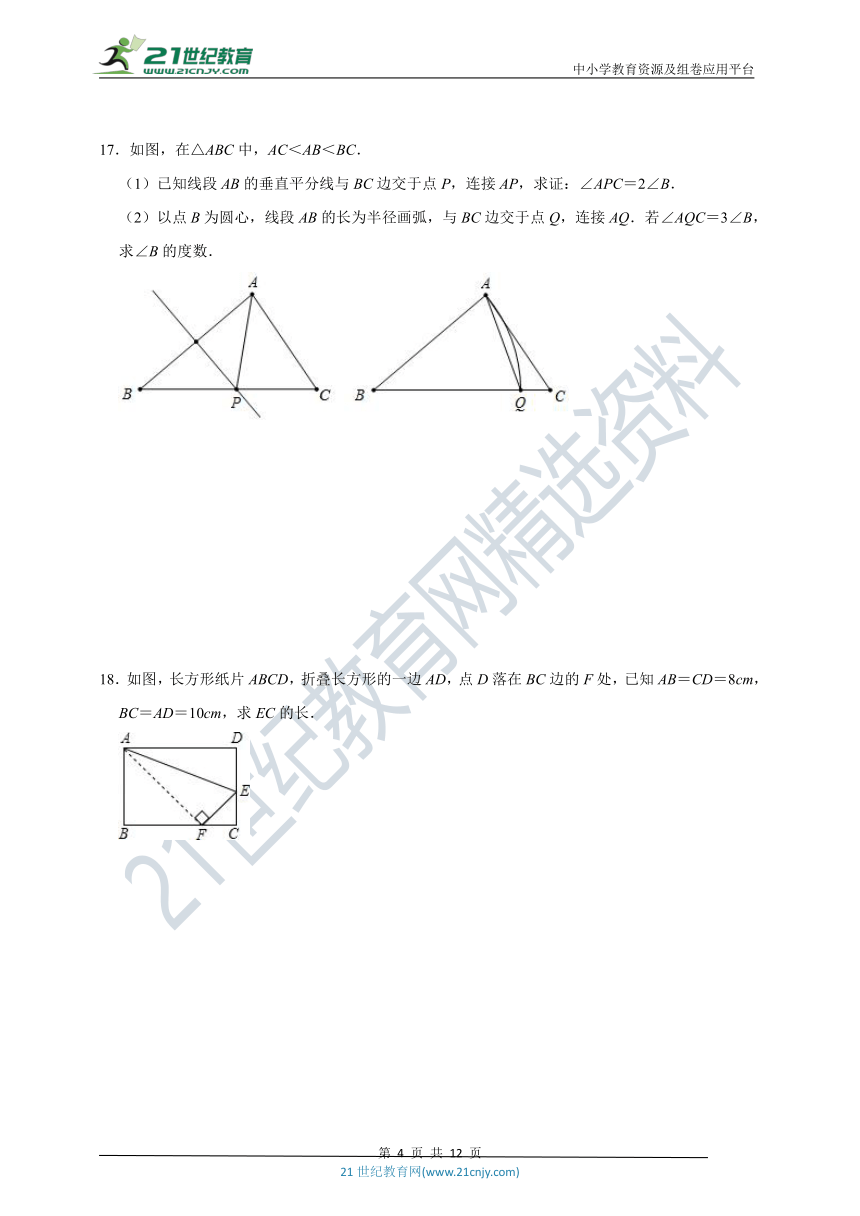
17.如图,在△ABC中,AC<AB<BC.
(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
18.如图,长方形纸片ABCD,折叠长方形的一边AD,点D落在BC边的F处,已知AB=CD=8cm,BC=AD=10cm,求EC的长.
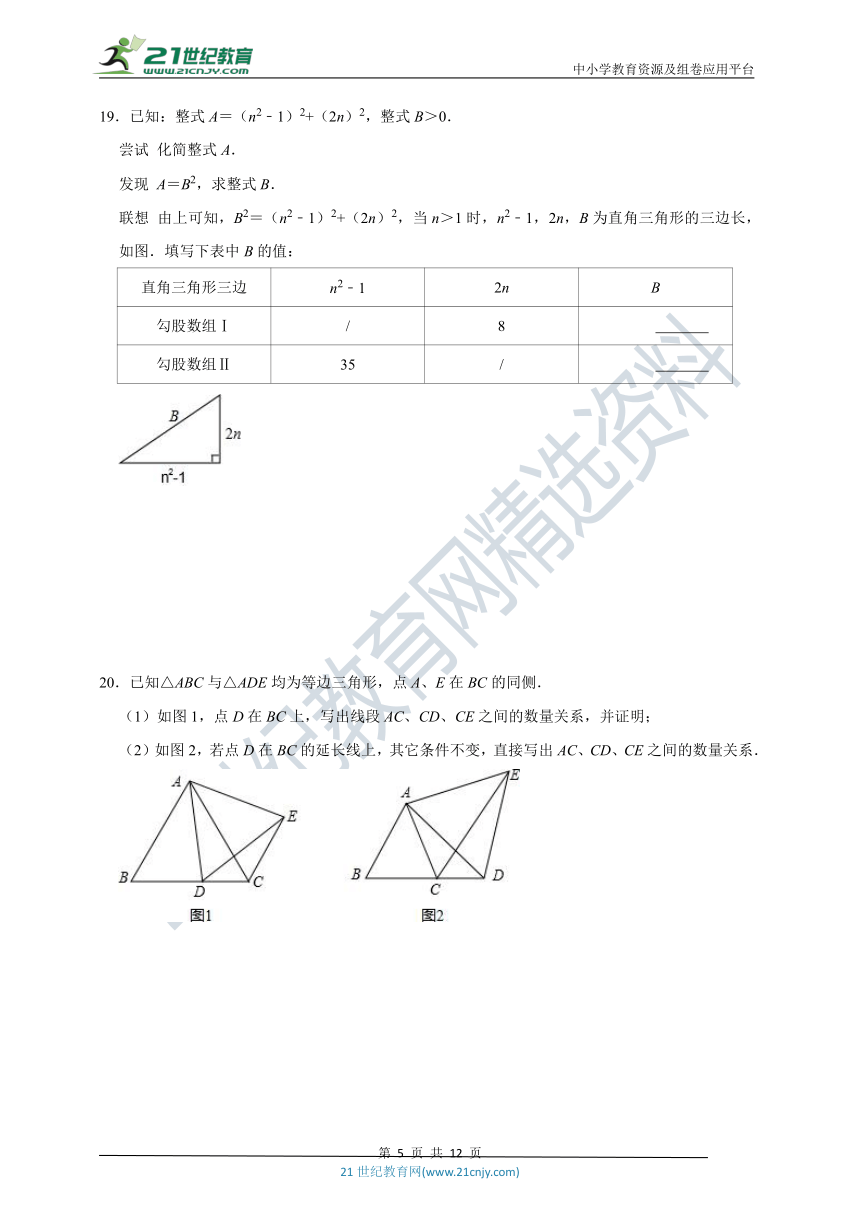
19.已知:整式A=(n2﹣1)2+(2n)2,整式B>0.
尝试
化简整式A.
发现
A=B2,求整式B.
联想
由上可知,B2=(n2﹣1)2+(2n)2,当n>1时,n2﹣1,2n,B为直角三角形的三边长,如图.填写下表中B的值:
直角三角形三边
n2﹣1
2n
B
勾股数组Ⅰ
/
8
勾股数组Ⅱ
35
/
20.已知△ABC与△ADE均为等边三角形,点A、E在BC的同侧.
(1)如图1,点D在BC上,写出线段AC、CD、CE之间的数量关系,并证明;
(2)如图2,若点D在BC的延长线上,其它条件不变,直接写出AC、CD、CE之间的数量关系.
试题解析
1.解:A、可利用勾股定理逆定理判定△ABC为直角三角形,故此选项不合题意;
B、根据勾股定理的逆定理可判断△ABC是直角三角形,故此选项不合题意;
C、根据三角形内角和定理可以计算出∠A=90°,△ABC为直角三角形,故此选项不合题意;
D、根据三角形内角和定理可以计算出∠A=45°,∠B=60°,∠C=75°,可判定△ABC不是直角三角形,故此选项符合题意;
故选:D.
2.解:∵AB∥CD,
∴∠1=∠ADC=30°,
又∵等腰直角三角形ADE中,∠ADE=45°,
∴∠1=45°﹣30°=15°,
故选:B.
3.解:如图作AH⊥CH.
在Rt△ACH中,∵AH=3,∠AHC=90°,∠ACH=30°,
∴AC=2AH=6,
在Rt△ABC中,AB===6.
故选:D.
4.解:A、∵直角三角形的斜边和一锐角对应相等,所以另一锐角必然相等,∴符合ASA定理,故本选项正确;
B、两边对应相等的两个直角三角形全等,若是两条直角边,可以根据SAS判定全等,若是直角边与斜边,可根据HL判定全等.故本选项正确;
C、有两个锐角相等的两个直角三角形相似,故本选项错误;
D、有一直角边和一锐角对应相等的两个直角三角形符合ASA定理,可判定相等,故本选项正确.
故选:C.
5.解:因为AB=9米,AC=12米,
根据勾股定理得BC==15米,
于是折断前树的高度是15+9=24米.
故选:D.
6.解:当8是直角边时,x==10,
当8是斜边时,x==2,
故选:C.
7.解:在△ABC中,∵∠B=30°,∠C=90°,
∴∠BAC=180°﹣∠B﹣∠C=60°,
由作图可知MN为AB的中垂线,
∴DA=DB,
∴∠DAB=∠B=30°,
∴∠CAD=∠BAC﹣∠DAB=30°,
故选:B.
8.解:此题要分情况讨论:当等腰三角形的顶角是钝角时,腰上的高在外部,
根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+20°=110°;
当等腰三角形的顶角是锐角时,腰上的高在其内部,
故顶角是90°﹣20°=70°.
故选:D.
9.解:过点E作EF⊥BC于F;如图所示:
则∠BFE=90°,
∵△ABC是等边三角形,∠B=60°,
∴∠FEB=90°﹣60°=30°,
∵BE=AB+AE=8+4=12,
∴BF=BE=6,
∴CF=BC﹣BF=2,
∵ED=EC,EF⊥BC,
∴DF=CF=2,
∴BD=BF﹣DF=4;
故选:B.
10.解:∵CF⊥AB,BE⊥AC,M为BC的中点,
∴EM=FM=BC=×8=4,
∴△EFM的周长=8+8+3=11.
故选:C.
11.解:例如:若α=50°,β=60°,则α+β>90°.
故答案为:若α=50°,β=60°,则α+β>90°.
12.解:∵∠ACB=90°,FD⊥AB,
∴∠ACB=∠FDB=90°,
∵∠F=30°,
∴∠A=∠F=30°(同角的余角相等).
又∵AB的垂直平分线DE交AC于E,
∴∠EBA=∠A=30°,
∴直角△DBE中,BE=2DE=2.
故答案是:2.
13.解:
①当∠A为顶角时,等腰三角形两底角的度数为:=50°
∴特征值k==
②当∠A为底角时,顶角的度数为:180°﹣80°﹣80°=20°
∴特征值k==
综上所述,特征值k为或
故答案为或
14.解:分两种情况:
①当点B′落在AD边上时,如图1,
∵四边形ABCD是矩形,
∴∠BAD=∠B=90°,
∵将△ABE沿AE折叠,点B的对应点B′落在AD边上,
∴∠BAE=∠B′AE=∠BAD=45°,
∴AB=BE,
∴a=1,
∴a=;
②当点B′落在CD边上时,如图2.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠C=∠D=90°,AD=BC=a.
∵将△ABE沿AE折叠,点B的对应点B′落在CD边上,
∴∠B=∠AB′E=90°,AB=AB′=1,EB=EB′=a,
∴DB′==,EC=BC﹣BE=a﹣a=a.
∵∠B'AD=∠EB'C=90°﹣∠AB'D,∠D=∠C=90°,
∴△ADB′∽△B′CE,
∴,
∴=
解得a1=,a2=﹣(舍去).
综上,所求a的值为或,
故选:C.
15.证明:在Rt△ABC和Rt△DCB中
,
∴Rt△ABC≌Rt△DCB(HL),
∴∠OBC=∠OCB,
∴BO=CO.
16.证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠F=90°,∠B+∠BDE=90°,
∵∠ADF=∠BDE,
∴∠F=∠ADF,
∴AD=AF.
17.解:(1)证明:∵线段AB的垂直平分线与BC边交于点P,
∴PA=PB,
∴∠B=∠BAP,
∵∠APC=∠B+∠BAP,
∴∠APC=2∠B;
(2)根据题意可知BA=BQ,
∴∠BAQ=∠BQA,
∵∠AQC=3∠B,∠AQC=∠B+∠BAQ,
∴∠BQA=2∠B,
∵∠BAQ+∠BQA+∠B=180°,
∴5∠B=180°,
∴∠B=36°.
18.解:依题意可得:BC=AD=AF=10,DE=EF.
在△ABF中,∠ABF=90°.
∴,
∴FC=10﹣6=4,
设EC=x,则EF=DE=8﹣x.
∵∠C=90°,
∴EC2+FC2=EF2,
∴x2+42=(8﹣x)2,
解之得:x=3,
∴EC=3(cm).
19.解:A=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2,
∵A=B2,B>0,
∴B=n2+1,
当2n=8时,n=4,∴n2+1=42+1=17;
当n2﹣1=35时,n2+1=37.
故答案为:17;37
20.(1)解:CD+CE=AC.理由如下:
∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵△ADE为等边三角形,
∴AD=AE,∠DAE=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△BAD和△CAE中
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+DC=CE+CD,
∴AC=CD+CE;
(2)解:CE﹣CD=AC.理由如下:
与(1)的证明方法一样可得到△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD﹣CD=CE﹣CD,
∴AC=CE﹣CD.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第17章
特殊三角形
综合能力提升卷
一、选择题(共10小题)
1.下列条件中,不能判断△ABC为直角三角形的是( )
A.a2=1,b2=2,c2=3
B.a:b:c=3:4:5
C.∠A+∠B=∠C
D.∠A:∠B:∠C=3:4:5
2.将等腰直角三角形纸片和矩形纸片按如图方式叠放在起,若∠1=30°,则∠2的度数为( )
A.10°
B.15°
C.20°
D.30°
3.将一个有45°角的三角尺的直角顶点C放在一张宽为3cm的纸带边沿上,另一个顶点A在纸带的另一边沿上,测得三角尺的一边AC与纸带的一边所在的直线成30°角,如图,则三角尺的最长边的长为( )
A.6
B.3
C.4
D.6
4.下列语句中不正确的是( )
A.斜边和一锐角对应相等的两个直角三角形全等
B.有两边对应相等的两个直角三角形全等
C.有两个锐角相等的两个直角三角形全等
D.有一直角边和一锐角对应相等的两个直角三角形全等
5.如图所示,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前( )米.
A.15
B.20
C.3
D.24
6.若一个直角三角形的三边长为6,8,x,则x的值是( )
A.10
B.2
C.10或2
D.7
7.如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交BC于点D,连接AD,则∠CAD的度数是( )
A.20°
B.30°
C.45°
D.60°
8.等腰三角形一腰上的高与另一腰的夹角为20°,则顶角的度数为( )
A.70°
B.55°
C.110°
D.70°或110°
9.如图,在等边△ABC中,AB=8,E是BA延长线上一点,且EA=4,D是BC上一点,且ED=EC,则BD的长为( )
A.3
B.4
C.5
D.6
10.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=3,BC=8,则△EFM的周长是( )
A.7
B.10
C.11
D.14
二、填空题(共4小题)
11.请举反例说明命题:“两个锐角的和是锐角”是假命题.反例如:
.
12.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是
.
13.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k=
.
14.如图,在矩形ABCD中,AB=1,BC=a,点E在边BC上,且BE=a.连接AE,将△ABE沿AE折叠,若点B的对应点B'落在矩形ABCD的边上,则a的值为( )
A.
B.
C.或
D.或
三、解答题(共6小题)
15.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
16.如图,已知在△ABC中,AB=AC,D是AB上一点,DE⊥BC,E是垂足,ED的延长线交CA的延长线于点F,
求证:AD=AF.
17.如图,在△ABC中,AC<AB<BC.
(1)已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.
(2)以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连接AQ.若∠AQC=3∠B,求∠B的度数.
18.如图,长方形纸片ABCD,折叠长方形的一边AD,点D落在BC边的F处,已知AB=CD=8cm,BC=AD=10cm,求EC的长.
19.已知:整式A=(n2﹣1)2+(2n)2,整式B>0.
尝试
化简整式A.
发现
A=B2,求整式B.
联想
由上可知,B2=(n2﹣1)2+(2n)2,当n>1时,n2﹣1,2n,B为直角三角形的三边长,如图.填写下表中B的值:
直角三角形三边
n2﹣1
2n
B
勾股数组Ⅰ
/
8
勾股数组Ⅱ
35
/
20.已知△ABC与△ADE均为等边三角形,点A、E在BC的同侧.
(1)如图1,点D在BC上,写出线段AC、CD、CE之间的数量关系,并证明;
(2)如图2,若点D在BC的延长线上,其它条件不变,直接写出AC、CD、CE之间的数量关系.
试题解析
1.解:A、可利用勾股定理逆定理判定△ABC为直角三角形,故此选项不合题意;
B、根据勾股定理的逆定理可判断△ABC是直角三角形,故此选项不合题意;
C、根据三角形内角和定理可以计算出∠A=90°,△ABC为直角三角形,故此选项不合题意;
D、根据三角形内角和定理可以计算出∠A=45°,∠B=60°,∠C=75°,可判定△ABC不是直角三角形,故此选项符合题意;
故选:D.
2.解:∵AB∥CD,
∴∠1=∠ADC=30°,
又∵等腰直角三角形ADE中,∠ADE=45°,
∴∠1=45°﹣30°=15°,
故选:B.
3.解:如图作AH⊥CH.
在Rt△ACH中,∵AH=3,∠AHC=90°,∠ACH=30°,
∴AC=2AH=6,
在Rt△ABC中,AB===6.
故选:D.
4.解:A、∵直角三角形的斜边和一锐角对应相等,所以另一锐角必然相等,∴符合ASA定理,故本选项正确;
B、两边对应相等的两个直角三角形全等,若是两条直角边,可以根据SAS判定全等,若是直角边与斜边,可根据HL判定全等.故本选项正确;
C、有两个锐角相等的两个直角三角形相似,故本选项错误;
D、有一直角边和一锐角对应相等的两个直角三角形符合ASA定理,可判定相等,故本选项正确.
故选:C.
5.解:因为AB=9米,AC=12米,
根据勾股定理得BC==15米,
于是折断前树的高度是15+9=24米.
故选:D.
6.解:当8是直角边时,x==10,
当8是斜边时,x==2,
故选:C.
7.解:在△ABC中,∵∠B=30°,∠C=90°,
∴∠BAC=180°﹣∠B﹣∠C=60°,
由作图可知MN为AB的中垂线,
∴DA=DB,
∴∠DAB=∠B=30°,
∴∠CAD=∠BAC﹣∠DAB=30°,
故选:B.
8.解:此题要分情况讨论:当等腰三角形的顶角是钝角时,腰上的高在外部,
根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+20°=110°;
当等腰三角形的顶角是锐角时,腰上的高在其内部,
故顶角是90°﹣20°=70°.
故选:D.
9.解:过点E作EF⊥BC于F;如图所示:
则∠BFE=90°,
∵△ABC是等边三角形,∠B=60°,
∴∠FEB=90°﹣60°=30°,
∵BE=AB+AE=8+4=12,
∴BF=BE=6,
∴CF=BC﹣BF=2,
∵ED=EC,EF⊥BC,
∴DF=CF=2,
∴BD=BF﹣DF=4;
故选:B.
10.解:∵CF⊥AB,BE⊥AC,M为BC的中点,
∴EM=FM=BC=×8=4,
∴△EFM的周长=8+8+3=11.
故选:C.
11.解:例如:若α=50°,β=60°,则α+β>90°.
故答案为:若α=50°,β=60°,则α+β>90°.
12.解:∵∠ACB=90°,FD⊥AB,
∴∠ACB=∠FDB=90°,
∵∠F=30°,
∴∠A=∠F=30°(同角的余角相等).
又∵AB的垂直平分线DE交AC于E,
∴∠EBA=∠A=30°,
∴直角△DBE中,BE=2DE=2.
故答案是:2.
13.解:
①当∠A为顶角时,等腰三角形两底角的度数为:=50°
∴特征值k==
②当∠A为底角时,顶角的度数为:180°﹣80°﹣80°=20°
∴特征值k==
综上所述,特征值k为或
故答案为或
14.解:分两种情况:
①当点B′落在AD边上时,如图1,
∵四边形ABCD是矩形,
∴∠BAD=∠B=90°,
∵将△ABE沿AE折叠,点B的对应点B′落在AD边上,
∴∠BAE=∠B′AE=∠BAD=45°,
∴AB=BE,
∴a=1,
∴a=;
②当点B′落在CD边上时,如图2.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠C=∠D=90°,AD=BC=a.
∵将△ABE沿AE折叠,点B的对应点B′落在CD边上,
∴∠B=∠AB′E=90°,AB=AB′=1,EB=EB′=a,
∴DB′==,EC=BC﹣BE=a﹣a=a.
∵∠B'AD=∠EB'C=90°﹣∠AB'D,∠D=∠C=90°,
∴△ADB′∽△B′CE,
∴,
∴=
解得a1=,a2=﹣(舍去).
综上,所求a的值为或,
故选:C.
15.证明:在Rt△ABC和Rt△DCB中
,
∴Rt△ABC≌Rt△DCB(HL),
∴∠OBC=∠OCB,
∴BO=CO.
16.证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠F=90°,∠B+∠BDE=90°,
∵∠ADF=∠BDE,
∴∠F=∠ADF,
∴AD=AF.
17.解:(1)证明:∵线段AB的垂直平分线与BC边交于点P,
∴PA=PB,
∴∠B=∠BAP,
∵∠APC=∠B+∠BAP,
∴∠APC=2∠B;
(2)根据题意可知BA=BQ,
∴∠BAQ=∠BQA,
∵∠AQC=3∠B,∠AQC=∠B+∠BAQ,
∴∠BQA=2∠B,
∵∠BAQ+∠BQA+∠B=180°,
∴5∠B=180°,
∴∠B=36°.
18.解:依题意可得:BC=AD=AF=10,DE=EF.
在△ABF中,∠ABF=90°.
∴,
∴FC=10﹣6=4,
设EC=x,则EF=DE=8﹣x.
∵∠C=90°,
∴EC2+FC2=EF2,
∴x2+42=(8﹣x)2,
解之得:x=3,
∴EC=3(cm).
19.解:A=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2,
∵A=B2,B>0,
∴B=n2+1,
当2n=8时,n=4,∴n2+1=42+1=17;
当n2﹣1=35时,n2+1=37.
故答案为:17;37
20.(1)解:CD+CE=AC.理由如下:
∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵△ADE为等边三角形,
∴AD=AE,∠DAE=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△BAD和△CAE中
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+DC=CE+CD,
∴AC=CD+CE;
(2)解:CE﹣CD=AC.理由如下:
与(1)的证明方法一样可得到△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD﹣CD=CE﹣CD,
∴AC=CE﹣CD.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
