人教版高一数学必修四 2.1平面向量的概念及其线性运算课件分解 课件(共41张PPT)
文档属性
| 名称 | 人教版高一数学必修四 2.1平面向量的概念及其线性运算课件分解 课件(共41张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览











文档简介
第1课时 平面向量的概念及其线性运算
(4)平行向量:方向相同或 的 向量;平行向 向量.规定:0与任一向量 .
(5)相等向量:长度 且方向 的向量.
(6)相反向量:长度 且方向 的向量.
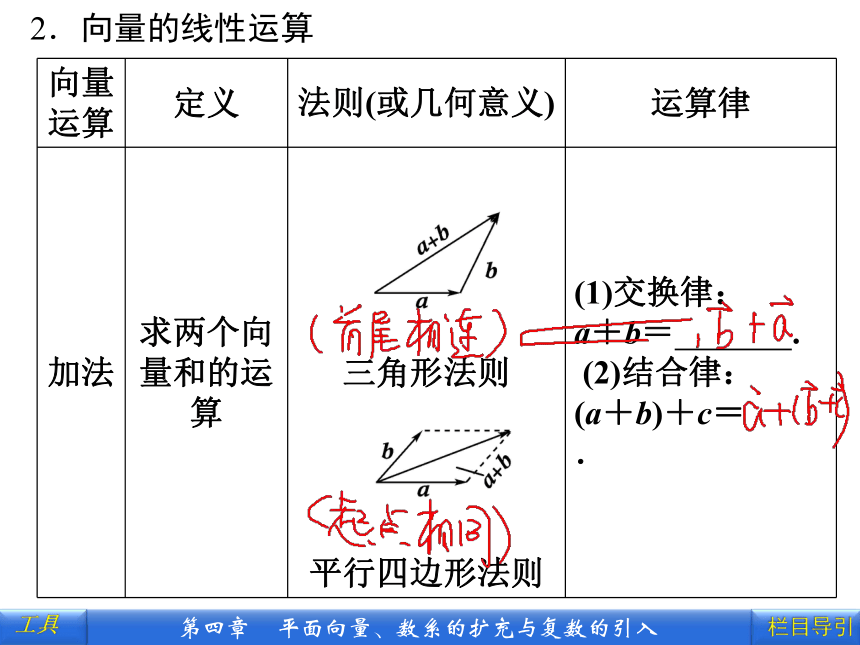
2.向量的线性运算
3.λ∈R,则下列命题正确的是( )
A.|λa|=λ|a| B.|λa|=|λ|a
C.|λa|=|λ||a| D.|λa|>0
解析: A中λ<0时不成立.B中|λa|是实数,而|λ|a是向量,故B错.D中,若λ=0或a=0时,|λa|=0,故D错.
答案: C
4.已知a与b是两个不共线向量,且向量a+λb与-(b-3a)共线,则λ=________.
给出下列命题:
(1)两个具有公共终点的向量,一定是共线向量.
(2)两个向量不能比较大小,但它们的模能比较大小.
(3)λa=0(λ为实数),则λ必为零.
(4)λ、μ为实数,若λa=μb,则a与b共线.
其中错误的命题的个数为( )
A.1 B.2 C.3 D.4
解析: (1)错.两向量共线要看其方向而不是起点与终点.
(2)对.因为向量既有大小,又有方向,故它们不能比较大小,但它们的模均为实数,故可以比较大小.
(3)错.当a=0时,不论λ为何值,λa=0.
(4)错.当λ=μ=0时,λa=μb,此时,a与b可以是任意向量.
答案: C
向量的线性运算要满足三角形法则和平行四边形法则,做题时,要注意三角形法则与平行四边形法则的要素.向量加法的三角形法则要素是“首尾相接,指向终点”,即第二个向量的起点与第一个向量的终点重合,和向量由第一个向量的起点指向第二个向量的终点;向量减法的三角形法则要素是“起点重合,指向被减向量”,即两个向量的起点重合,差向量由减向量的终点指向被减向量的终点;平行四边形法则的要素是“起点重合”,即两个向量的起点相同,和向量的起点也相同.
1.向量共线的充要条件中要注意当两向量共线时,通常只有非零向量才能表示与之共线的其他向量,要注意待定系数法的运用和方程思想.
2.证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得到三点共线.
4.共线定理的作用:用向量共线定理可以证明几何中的三点共线和直线平行问题.但是向量平行与直线平行是有区别的,直线平行不包括重合的情况.要证明三点共线或直线平行都是先探索有关的向量满足向量等式b=λa,再结合条件或图形有无公共点证明几何位置.
从近两年的高考试题来看,向量的线性运算、共线问题是高考的热点.尤其向量的线性运算出现的频率较高,多以选择题、填空题的形式出现,属中低档题目,主要考查向量的线性运算及对向量有关概念的理解,常与向量共线和平面向量基本定理交汇命题.
【阅后报告】 解答本题的难点是不知角平分线定理,只要把BD和DA的关系用BC和CA表示,问题便可解决.
3.(2009·北京卷)已知向量a、b不共线,c=ka+b(k∈R),d=a-b.如果c∥d,那么( )
A.k=1且c与d同向 B.k=1且c与d反向
C.k=-1且c与d同向 D.k=-1且c与d反向
第四章
4.1平面向量的概念及线性运算
1.了解平面向量的基本定理及其意义.
2.掌握平面向量的正交分解及其坐标表示.
3.会用坐标表示平面向量的加法、减法与数乘运算.
4.会用坐标表示平面向量共线的条件.
平面向量的基本定理及坐标运算
1.了解向量的实际背景.
2.理解平面向量的概念和向量相等的含义.
3.理解向量的几何表示.
4.掌握向量加法、减法的运算,并理解其几何意义.
5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.
6.了解向量线性运算的性质及其几何意义.
平面向量的概念及其线性运算
考纲下载
知识点
1.理解复数的基本概念.
2.理解复数相等的充要条件.
3.了解复数的代数表示法及其几何意义.
4.会进行复数代数形式的四则运算.
5.了解复数代数形式的加、减运算的几何意义.
数系的扩充与复数的引入
1.理解平面向量数量积的含义及其物理意义.
2.了解平面向量的数量积与向量投影的关系.
3.掌握数量积的坐标表达式,会进行平面向量数量积的坐标运算.
4.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.
5.会用向量方法解决某些简单的力学问题和其他一些实际问题.
平面向量的数量积及平面向量应用举例
考纲下载
知识点
1.向量的有关概念
(1)向量:既有 又有 的量叫做向量,向量的大小叫做向量的 .
(2)零向量: 的向量叫做零向量,其方向是 的,零向量记作 .
(3)单位向量:与向量a同方向,且长度为 的向量,叫做a方向上的单位向量,记作a0.
(1)交换律:
a+b= .
(2)结合律:
(a+b)+c= .
三角形法则
平行四边形法则
求两个向量和的运算
加法
运算律
法则(或几何意义)
定义
向量
运算
λ(μa)=
(λ+μ)a=
;
λ(a+b)=
.
(1)|λa|= .
(2)
当λ>0时,λa与a的方向 ;
当λ<0时,λa与a的方向 ;
当λ=0时,λa=0.
求实数λ与向量a的积的运算
数乘
a-b=a+(-b)
三角形法则
求a与b的相反向量-b的和的运算叫做a与b的差
减法
运算律
法则(或几何意义)
定义
向量
运算
答案: C
答案: A
答案: 2
答案: B
答案: B
(4)平行向量:方向相同或 的 向量;平行向 向量.规定:0与任一向量 .
(5)相等向量:长度 且方向 的向量.
(6)相反向量:长度 且方向 的向量.
2.向量的线性运算
3.λ∈R,则下列命题正确的是( )
A.|λa|=λ|a| B.|λa|=|λ|a
C.|λa|=|λ||a| D.|λa|>0
解析: A中λ<0时不成立.B中|λa|是实数,而|λ|a是向量,故B错.D中,若λ=0或a=0时,|λa|=0,故D错.
答案: C
4.已知a与b是两个不共线向量,且向量a+λb与-(b-3a)共线,则λ=________.
给出下列命题:
(1)两个具有公共终点的向量,一定是共线向量.
(2)两个向量不能比较大小,但它们的模能比较大小.
(3)λa=0(λ为实数),则λ必为零.
(4)λ、μ为实数,若λa=μb,则a与b共线.
其中错误的命题的个数为( )
A.1 B.2 C.3 D.4
解析: (1)错.两向量共线要看其方向而不是起点与终点.
(2)对.因为向量既有大小,又有方向,故它们不能比较大小,但它们的模均为实数,故可以比较大小.
(3)错.当a=0时,不论λ为何值,λa=0.
(4)错.当λ=μ=0时,λa=μb,此时,a与b可以是任意向量.
答案: C
向量的线性运算要满足三角形法则和平行四边形法则,做题时,要注意三角形法则与平行四边形法则的要素.向量加法的三角形法则要素是“首尾相接,指向终点”,即第二个向量的起点与第一个向量的终点重合,和向量由第一个向量的起点指向第二个向量的终点;向量减法的三角形法则要素是“起点重合,指向被减向量”,即两个向量的起点重合,差向量由减向量的终点指向被减向量的终点;平行四边形法则的要素是“起点重合”,即两个向量的起点相同,和向量的起点也相同.
1.向量共线的充要条件中要注意当两向量共线时,通常只有非零向量才能表示与之共线的其他向量,要注意待定系数法的运用和方程思想.
2.证明三点共线问题,可用向量共线来解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得到三点共线.
4.共线定理的作用:用向量共线定理可以证明几何中的三点共线和直线平行问题.但是向量平行与直线平行是有区别的,直线平行不包括重合的情况.要证明三点共线或直线平行都是先探索有关的向量满足向量等式b=λa,再结合条件或图形有无公共点证明几何位置.
从近两年的高考试题来看,向量的线性运算、共线问题是高考的热点.尤其向量的线性运算出现的频率较高,多以选择题、填空题的形式出现,属中低档题目,主要考查向量的线性运算及对向量有关概念的理解,常与向量共线和平面向量基本定理交汇命题.
【阅后报告】 解答本题的难点是不知角平分线定理,只要把BD和DA的关系用BC和CA表示,问题便可解决.
3.(2009·北京卷)已知向量a、b不共线,c=ka+b(k∈R),d=a-b.如果c∥d,那么( )
A.k=1且c与d同向 B.k=1且c与d反向
C.k=-1且c与d同向 D.k=-1且c与d反向
第四章
4.1平面向量的概念及线性运算
1.了解平面向量的基本定理及其意义.
2.掌握平面向量的正交分解及其坐标表示.
3.会用坐标表示平面向量的加法、减法与数乘运算.
4.会用坐标表示平面向量共线的条件.
平面向量的基本定理及坐标运算
1.了解向量的实际背景.
2.理解平面向量的概念和向量相等的含义.
3.理解向量的几何表示.
4.掌握向量加法、减法的运算,并理解其几何意义.
5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.
6.了解向量线性运算的性质及其几何意义.
平面向量的概念及其线性运算
考纲下载
知识点
1.理解复数的基本概念.
2.理解复数相等的充要条件.
3.了解复数的代数表示法及其几何意义.
4.会进行复数代数形式的四则运算.
5.了解复数代数形式的加、减运算的几何意义.
数系的扩充与复数的引入
1.理解平面向量数量积的含义及其物理意义.
2.了解平面向量的数量积与向量投影的关系.
3.掌握数量积的坐标表达式,会进行平面向量数量积的坐标运算.
4.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.
5.会用向量方法解决某些简单的力学问题和其他一些实际问题.
平面向量的数量积及平面向量应用举例
考纲下载
知识点
1.向量的有关概念
(1)向量:既有 又有 的量叫做向量,向量的大小叫做向量的 .
(2)零向量: 的向量叫做零向量,其方向是 的,零向量记作 .
(3)单位向量:与向量a同方向,且长度为 的向量,叫做a方向上的单位向量,记作a0.
(1)交换律:
a+b= .
(2)结合律:
(a+b)+c= .
三角形法则
平行四边形法则
求两个向量和的运算
加法
运算律
法则(或几何意义)
定义
向量
运算
λ(μa)=
(λ+μ)a=
;
λ(a+b)=
.
(1)|λa|= .
(2)
当λ>0时,λa与a的方向 ;
当λ<0时,λa与a的方向 ;
当λ=0时,λa=0.
求实数λ与向量a的积的运算
数乘
a-b=a+(-b)
三角形法则
求a与b的相反向量-b的和的运算叫做a与b的差
减法
运算律
法则(或几何意义)
定义
向量
运算
答案: C
答案: A
答案: 2
答案: B
答案: B
