人教版高一数学必修四 2.2 平面向量的线性运算复习课课件课件(共26张PPT)
文档属性
| 名称 | 人教版高一数学必修四 2.2 平面向量的线性运算复习课课件课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览






文档简介
复习目标:
1、掌握向量加、减法的运算,并理解其几何意义.
2、掌握向量数乘运算,并理解其几何意义,以及两个向量共线的含义.
3、了解向量的线性运算性质及其几何意义.
二、合作共享 交流提升
三、案例剖析 总结规律
例3、如图,设?ABCD一边AB的四等分点中最靠近B的一点为E,对角线BD的五等分点中靠近B的一点为F,求证:E、F、C三点在一条直线上.
四、反馈矫正 形成能力
学案导学
自主建构
合作共享
交流提升
案例剖析
总结规律
反馈矫正
形成能力
课堂小结
布置作业
2.2 平面向量的线性运算(复习课)
重点:向量加、减、数乘运算及其几何意义.
难点:应用向量线性运算的定义、性质灵活解决相应的 问题.
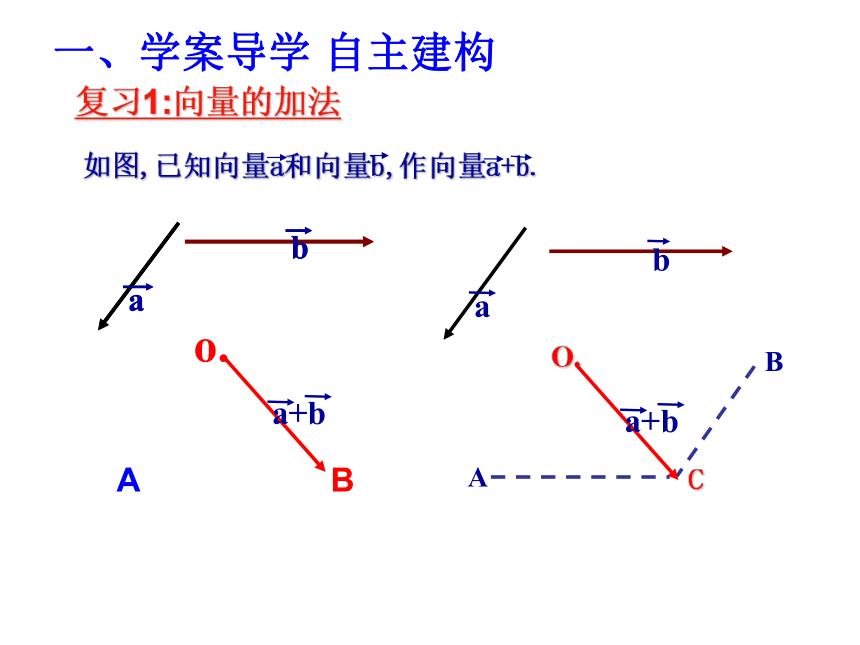
复习1:向量的加法
B
A
如图,已知向量a和向量b,作向量a+b.
b
a
o.
O.
C
a+b
b
a
A
B
b
a+b
a
一、学案导学 自主建构
向量加法的运算法则
⑴. 对于零向量和任一向量 ,有
⑵对于相反向量,有
⑶加法交换律
⑷加法结合律
O
A
B
C
向量加法的平行四边形法则
O
A
B
C
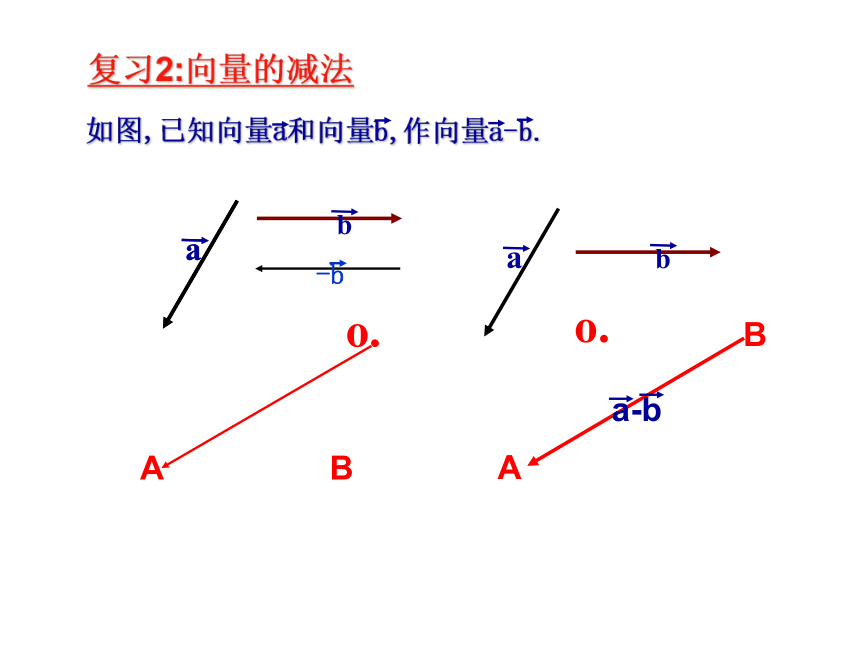
复习2:向量的减法
o.
B
A
a-b
如图,已知向量a和向量b,作向量a-b.
a
b
a
-b
o.
B
A
a
b
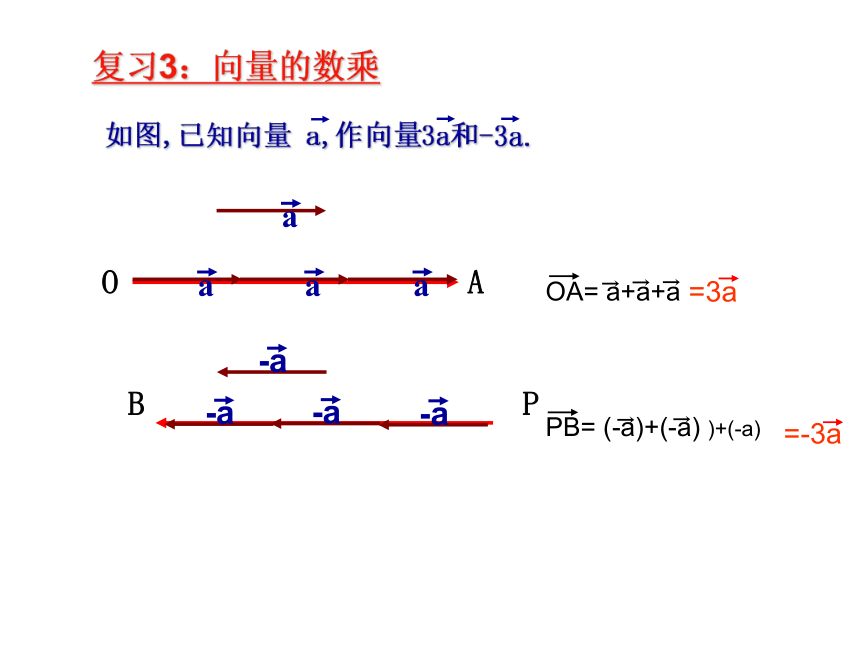
复习3:向量的数乘
O
A
P
B
-a
如图,已知向量 a,作向量3a和-3a.
a
a
-a
a
a
-a
OA= a+a+a
PB= (-a)+(-a) )+(-a)
=3a
=-3a
-a
向量的数乘运算满足如下运算律:
a∥b
a=λb (λ∈R且b≠0)
向量表示:
复习4:平面向量共线定理
向量b与非零向量a共线的充分必要条件是有且只有一个实数λ,使得b=λa .
1、填空题:
90°
2、判断题:
(1)相反向量就是方向相反的向量
(2)
(3)
(4) 在△ABC中,必有
(5)若 ,
则A、B、C三点必是一个三角形的三个顶点。
( 错 )
(对 )
(错)
(错)
(对 )
例1:根据条件判断下列四边形的形状
平行四边形ABCD
梯形ABCD
例2、
如图,在 中,延长BA到C,使AC=BA,在OB上取
点D,使BD= OB.DC与OA交于E,设 请用
.
E
C
O
D
B
A
分析: 解题的关键是建立
的联系,为此需要利用向量的加、减法数乘运算。
解:因为A是BC的中点,所以
图1
跟踪训练:
1、有一边长为1的正方形ABCD,设
求:
D
C
A
B
E
O
F
G
2、已知A、B、C是不共线的三点,O是
△ABC内的一点,若 = 0,
则O 是△ABC的——————
(填内心、重心、垂心、外心等).
1.外心:三角形三条垂直平分线的交点
2.内心:三角形三条角平分线的交点
3.垂心:三角形三条高线的交点
4. 重心:三角形三条中线的交点
3、
二、知识应用:
1、求向量加、减、数乘运算
2.共线向量定理的应用:
(1)证明 向量共线;
(2)证明 三点共线: AB=λBC A,B,C三点共线;
(3)证明 两直线平行:
AB=λCD AB∥CD
AB、CD不重合
直线AB∥直线CD
一、概念与定理
① 向量加、减、数乘的定义、几何意义及运算律
② 向量共线定理 ( a≠0 )
b=λa 向量a与b共线
五、课堂小结 布置作业
课下作业:
C.
A.
B.
2.
设 是非零向量, 是非零实数,下列结论正确的是( ).
D.
1.
下列四个说法正确的个数有( ).
B.2个
A.1个
C.3个
D.4个
?
?
?
?
B
C
5
D
3.矩形ABCD中, , .则
.
4.已知 表示向东走5 km, 表示向北走 5km,则 表示______________________
向北偏东60?方向走10km
5.在矩形ABCD中, , 。则向量 的长度等于 ( )
A.2
B.
C.3
D.4
A
7.如图D、E、F分别为△ABC的边AB、BC、CA的中点,则下列等式正确的是 ( )
A.
B.
C.
D.
D
A
B
C
D
E
F
6.在 ABCD中, 等于 ( )
A.
B.
C.
D.
8. , , 为非零向量,且 平分 与 的夹角,则……………………( )
B
A.
B.
C.
D.以上都不对
=
=
⊥
9、O是平面内一定点,A、B、C是平面内
不共线的三个点,动点P满足
则P的轨迹一定通过△ABC的——心.
内心
10: 如图,在平行四边形ABCD中,点M是AB中点,点
N在线段BD上,且有BN= BD,求证:M、N、C
三点共线。
提示:设AB = a BC = b
则MN= … = a + b
MC= … = a+ b
复习目标:
1、掌握向量加、减法的运算,并理解其几何意义.
2、掌握向量数乘运算,并理解其几何意义,以及两个向量共线的含义.
3、了解向量的线性运算性质及其几何意义.
二、合作共享 交流提升
三、案例剖析 总结规律
例3、如图,设?ABCD一边AB的四等分点中最靠近B的一点为E,对角线BD的五等分点中靠近B的一点为F,求证:E、F、C三点在一条直线上.
四、反馈矫正 形成能力
a∥b
a=λb (λ∈R且b≠0)
向量表示:
复习4:平面向量共线定理
向量b与非零向量a共线的充分必要条件是有且只有一个实数λ,使得b=λa .
复习目标:
1、掌握向量加、减法的运算,并理解其几何意义.
2、掌握向量数乘运算,并理解其几何意义,以及两个向量共线的含义.
3、了解向量的线性运算性质及其几何意义.
二、合作共享 交流提升
三、案例剖析 总结规律
例3、如图,设?ABCD一边AB的四等分点中最靠近B的一点为E,对角线BD的五等分点中靠近B的一点为F,求证:E、F、C三点在一条直线上.
四、反馈矫正 形成能力
2.2 平面向量的线性运算(复习课)
1、掌握向量加、减法的运算,并理解其几何意义.
2、掌握向量数乘运算,并理解其几何意义,以及两个向量共线的含义.
3、了解向量的线性运算性质及其几何意义.
二、合作共享 交流提升
三、案例剖析 总结规律
例3、如图,设?ABCD一边AB的四等分点中最靠近B的一点为E,对角线BD的五等分点中靠近B的一点为F,求证:E、F、C三点在一条直线上.
四、反馈矫正 形成能力
学案导学
自主建构
合作共享
交流提升
案例剖析
总结规律
反馈矫正
形成能力
课堂小结
布置作业
2.2 平面向量的线性运算(复习课)
重点:向量加、减、数乘运算及其几何意义.
难点:应用向量线性运算的定义、性质灵活解决相应的 问题.
复习1:向量的加法
B
A
如图,已知向量a和向量b,作向量a+b.
b
a
o.
O.
C
a+b
b
a
A
B
b
a+b
a
一、学案导学 自主建构
向量加法的运算法则
⑴. 对于零向量和任一向量 ,有
⑵对于相反向量,有
⑶加法交换律
⑷加法结合律
O
A
B
C
向量加法的平行四边形法则
O
A
B
C
复习2:向量的减法
o.
B
A
a-b
如图,已知向量a和向量b,作向量a-b.
a
b
a
-b
o.
B
A
a
b
复习3:向量的数乘
O
A
P
B
-a
如图,已知向量 a,作向量3a和-3a.
a
a
-a
a
a
-a
OA= a+a+a
PB= (-a)+(-a) )+(-a)
=3a
=-3a
-a
向量的数乘运算满足如下运算律:
a∥b
a=λb (λ∈R且b≠0)
向量表示:
复习4:平面向量共线定理
向量b与非零向量a共线的充分必要条件是有且只有一个实数λ,使得b=λa .
1、填空题:
90°
2、判断题:
(1)相反向量就是方向相反的向量
(2)
(3)
(4) 在△ABC中,必有
(5)若 ,
则A、B、C三点必是一个三角形的三个顶点。
( 错 )
(对 )
(错)
(错)
(对 )
例1:根据条件判断下列四边形的形状
平行四边形ABCD
梯形ABCD
例2、
如图,在 中,延长BA到C,使AC=BA,在OB上取
点D,使BD= OB.DC与OA交于E,设 请用
.
E
C
O
D
B
A
分析: 解题的关键是建立
的联系,为此需要利用向量的加、减法数乘运算。
解:因为A是BC的中点,所以
图1
跟踪训练:
1、有一边长为1的正方形ABCD,设
求:
D
C
A
B
E
O
F
G
2、已知A、B、C是不共线的三点,O是
△ABC内的一点,若 = 0,
则O 是△ABC的——————
(填内心、重心、垂心、外心等).
1.外心:三角形三条垂直平分线的交点
2.内心:三角形三条角平分线的交点
3.垂心:三角形三条高线的交点
4. 重心:三角形三条中线的交点
3、
二、知识应用:
1、求向量加、减、数乘运算
2.共线向量定理的应用:
(1)证明 向量共线;
(2)证明 三点共线: AB=λBC A,B,C三点共线;
(3)证明 两直线平行:
AB=λCD AB∥CD
AB、CD不重合
直线AB∥直线CD
一、概念与定理
① 向量加、减、数乘的定义、几何意义及运算律
② 向量共线定理 ( a≠0 )
b=λa 向量a与b共线
五、课堂小结 布置作业
课下作业:
C.
A.
B.
2.
设 是非零向量, 是非零实数,下列结论正确的是( ).
D.
1.
下列四个说法正确的个数有( ).
B.2个
A.1个
C.3个
D.4个
?
?
?
?
B
C
5
D
3.矩形ABCD中, , .则
.
4.已知 表示向东走5 km, 表示向北走 5km,则 表示______________________
向北偏东60?方向走10km
5.在矩形ABCD中, , 。则向量 的长度等于 ( )
A.2
B.
C.3
D.4
A
7.如图D、E、F分别为△ABC的边AB、BC、CA的中点,则下列等式正确的是 ( )
A.
B.
C.
D.
D
A
B
C
D
E
F
6.在 ABCD中, 等于 ( )
A.
B.
C.
D.
8. , , 为非零向量,且 平分 与 的夹角,则……………………( )
B
A.
B.
C.
D.以上都不对
=
=
⊥
9、O是平面内一定点,A、B、C是平面内
不共线的三个点,动点P满足
则P的轨迹一定通过△ABC的——心.
内心
10: 如图,在平行四边形ABCD中,点M是AB中点,点
N在线段BD上,且有BN= BD,求证:M、N、C
三点共线。
提示:设AB = a BC = b
则MN= … = a + b
MC= … = a+ b
复习目标:
1、掌握向量加、减法的运算,并理解其几何意义.
2、掌握向量数乘运算,并理解其几何意义,以及两个向量共线的含义.
3、了解向量的线性运算性质及其几何意义.
二、合作共享 交流提升
三、案例剖析 总结规律
例3、如图,设?ABCD一边AB的四等分点中最靠近B的一点为E,对角线BD的五等分点中靠近B的一点为F,求证:E、F、C三点在一条直线上.
四、反馈矫正 形成能力
a∥b
a=λb (λ∈R且b≠0)
向量表示:
复习4:平面向量共线定理
向量b与非零向量a共线的充分必要条件是有且只有一个实数λ,使得b=λa .
复习目标:
1、掌握向量加、减法的运算,并理解其几何意义.
2、掌握向量数乘运算,并理解其几何意义,以及两个向量共线的含义.
3、了解向量的线性运算性质及其几何意义.
二、合作共享 交流提升
三、案例剖析 总结规律
例3、如图,设?ABCD一边AB的四等分点中最靠近B的一点为E,对角线BD的五等分点中靠近B的一点为F,求证:E、F、C三点在一条直线上.
四、反馈矫正 形成能力
2.2 平面向量的线性运算(复习课)
