冀教版数学八年级上13.3 第3课时 运用“角边角”(ASA)及“角角边”(AAS)判定三角形全等 导学案(含答案)
文档属性
| 名称 | 冀教版数学八年级上13.3 第3课时 运用“角边角”(ASA)及“角角边”(AAS)判定三角形全等 导学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 104.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 00:00:00 | ||
图片预览


文档简介
13.3
全等三角形的判定
第3课时
运用“角边角”(ASA)及“角角边”(AAS)判定三角形全等
学习目标:
1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.
2.会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.
学习重点:三角形全等的判定方法“ASA”和“AAS”.
学习难点:用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.
知识链接
1.如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?
如果可以,带哪块去合适?
你能说明其中理由吗?
答:__________________________________________________________________________.
二、新知预习
2.如图,在△ABC和△A'B'C'中,∠B=∠B',BC=B'C',∠C=∠C'.把△ABC和△A'B'C'叠放在一起,它们能够完全重合吗?提出你的猜想,并试着说明理由.
验证如下:将△ABC叠放在△A'B'C'上,使边BC落在边____上,顶点A与顶点____在边B'C'同侧,由____=____,可得边BC与边B'C'完全重合,因为∠B=∠B',∠C=∠C',∠B的另一边BA落在边B'A'上,∠C的另一边落在边C'A'上,所以____与____完全重合,____与____完全重合,由于“____”,所以点____与点____重合.
所以,△ABC____△A'B'C'.
于是我们得到关于三角形全等的另一个基本事实:
基本事实三
如果两个三角形的两个角和它们的夹边对应相等,那么这个两个三角形全等.
全等三角形和判定定理
如果两个三角形的两边及其中一个角的对边对应相等,那么这两个三角对应全等.
自学自测
1.有△ABC和△DEF,下列各组条件中,若能判定这两个三角形全等,在后面的括号内打“√”,若不能,则在后面的括号内打“×”.
(1)AB=DE,BC=EF,∠B=∠E.( )
(2)AB=DE,BC=EF,CA=FD.( )
(3)∠A=∠D,∠B=∠E,CA=FD.( )
(4)AB=DE,∠A=∠D,BC=EF.( )
(5)∠A=∠D,∠B=∠E,∠C=∠F.( )
2.已知:如图,AD=BE,∠A=∠FDE,BC∥EF.
求证:△ABC≌△DEF.
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
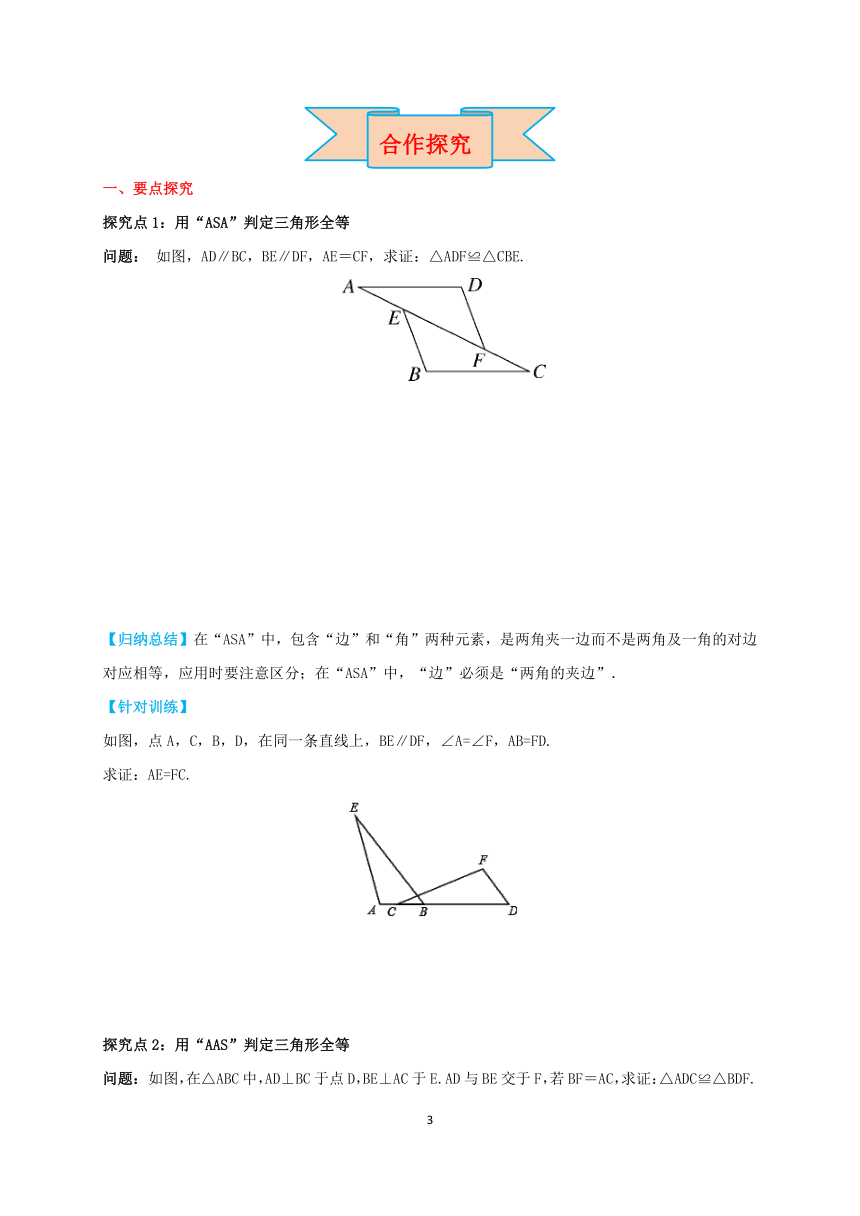
探究点1:用“ASA”判定三角形全等
问题:
如图,AD∥BC,BE∥DF,AE=CF,求证:△ADF≌△CBE.
【归纳总结】在“ASA”中,包含“边”和“角”两种元素,是两角夹一边而不是两角及一角的对边对应相等,应用时要注意区分;在“ASA”中,“边”必须是“两角的夹边”.
【针对训练】
如图,点A,C,B,D,在同一条直线上,BE∥DF,∠A=∠F,AB=FD.
求证:AE=FC.
探究点2:用“AAS”判定三角形全等
问题:
如图,在△ABC中,AD⊥BC于点D,BE⊥AC于E.AD与BE交于F,若BF=AC,求证:△ADC≌△BDF.
【归纳总结】在“ASA”中,包含“边”和“角”两种元素,是两角夹一边而不是两角及一角的对边对应相等,应用时要注意区分;在“ASA”中,“边”必须是“两角的夹边”.
【针对训练】
已知:如图,点A,B,D,E,在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=DF.
二、课堂小结
内容
联系
“角边角”
两角和它们的________对应相等的两个三角形全等.简记为“角边角”或“________”
两个三角形,如果具备两个角和一边对应相等,就可判定其全等,但其中“对应”必不可少,也就是说假如一个三角形中相等的边是两角的夹边,而另一个三角形中相等的边是其中一等角的对边,则这两个三角形不一定全等
在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′(ASA)
“角角边”
两个角和其中一个角的________对应相等的两个三角形全等.简记为“角角边”或“________”
在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′(AAS)
易错提醒
三个角分别相等的两个三角形________全等(填“一定”或“不一定”)
1.如图∠ACB=∠DFE,BC=EF,那么应补充一个条件___________,才能使△ABC≌△DEF
(写出一个即可).
2.
如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判别下面的两个三角形是否全等,并说明理由.
3.已知:如图,
AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.
4.已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.E.求证:(1)△BDA≌△AEC;(2)DE=BD+CE.
当堂检测参考答案:
1.∠B=∠E或∠A=∠D或
AC=DF
2.不全等,因为BC虽然是公共边,但不是对应边.
3.证明:
∵
AB⊥BC,AD⊥DC,
∴
∠
B=∠D=90
°.
在△ABC和△ADC中,
∠1=∠2
(已知),
∠
B=∠D(已证),
AC=AC
(公共边),
∴
△ABC≌△ADC(AAS),
∴AB=AD.
(1)∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE.
在△BDA和△AEC中,
∵
∴△BDA≌△AEC(AAS);
∵△BDA≌△AEC,
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
1
全等三角形的判定
第3课时
运用“角边角”(ASA)及“角角边”(AAS)判定三角形全等
学习目标:
1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.
2.会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.
学习重点:三角形全等的判定方法“ASA”和“AAS”.
学习难点:用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.
知识链接
1.如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?
如果可以,带哪块去合适?
你能说明其中理由吗?
答:__________________________________________________________________________.
二、新知预习
2.如图,在△ABC和△A'B'C'中,∠B=∠B',BC=B'C',∠C=∠C'.把△ABC和△A'B'C'叠放在一起,它们能够完全重合吗?提出你的猜想,并试着说明理由.
验证如下:将△ABC叠放在△A'B'C'上,使边BC落在边____上,顶点A与顶点____在边B'C'同侧,由____=____,可得边BC与边B'C'完全重合,因为∠B=∠B',∠C=∠C',∠B的另一边BA落在边B'A'上,∠C的另一边落在边C'A'上,所以____与____完全重合,____与____完全重合,由于“____”,所以点____与点____重合.
所以,△ABC____△A'B'C'.
于是我们得到关于三角形全等的另一个基本事实:
基本事实三
如果两个三角形的两个角和它们的夹边对应相等,那么这个两个三角形全等.
全等三角形和判定定理
如果两个三角形的两边及其中一个角的对边对应相等,那么这两个三角对应全等.
自学自测
1.有△ABC和△DEF,下列各组条件中,若能判定这两个三角形全等,在后面的括号内打“√”,若不能,则在后面的括号内打“×”.
(1)AB=DE,BC=EF,∠B=∠E.( )
(2)AB=DE,BC=EF,CA=FD.( )
(3)∠A=∠D,∠B=∠E,CA=FD.( )
(4)AB=DE,∠A=∠D,BC=EF.( )
(5)∠A=∠D,∠B=∠E,∠C=∠F.( )
2.已知:如图,AD=BE,∠A=∠FDE,BC∥EF.
求证:△ABC≌△DEF.
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:用“ASA”判定三角形全等
问题:
如图,AD∥BC,BE∥DF,AE=CF,求证:△ADF≌△CBE.
【归纳总结】在“ASA”中,包含“边”和“角”两种元素,是两角夹一边而不是两角及一角的对边对应相等,应用时要注意区分;在“ASA”中,“边”必须是“两角的夹边”.
【针对训练】
如图,点A,C,B,D,在同一条直线上,BE∥DF,∠A=∠F,AB=FD.
求证:AE=FC.
探究点2:用“AAS”判定三角形全等
问题:
如图,在△ABC中,AD⊥BC于点D,BE⊥AC于E.AD与BE交于F,若BF=AC,求证:△ADC≌△BDF.
【归纳总结】在“ASA”中,包含“边”和“角”两种元素,是两角夹一边而不是两角及一角的对边对应相等,应用时要注意区分;在“ASA”中,“边”必须是“两角的夹边”.
【针对训练】
已知:如图,点A,B,D,E,在同一直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=DF.
二、课堂小结
内容
联系
“角边角”
两角和它们的________对应相等的两个三角形全等.简记为“角边角”或“________”
两个三角形,如果具备两个角和一边对应相等,就可判定其全等,但其中“对应”必不可少,也就是说假如一个三角形中相等的边是两角的夹边,而另一个三角形中相等的边是其中一等角的对边,则这两个三角形不一定全等
在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′(ASA)
“角角边”
两个角和其中一个角的________对应相等的两个三角形全等.简记为“角角边”或“________”
在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′(AAS)
易错提醒
三个角分别相等的两个三角形________全等(填“一定”或“不一定”)
1.如图∠ACB=∠DFE,BC=EF,那么应补充一个条件___________,才能使△ABC≌△DEF
(写出一个即可).
2.
如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判别下面的两个三角形是否全等,并说明理由.
3.已知:如图,
AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.
4.已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.E.求证:(1)△BDA≌△AEC;(2)DE=BD+CE.
当堂检测参考答案:
1.∠B=∠E或∠A=∠D或
AC=DF
2.不全等,因为BC虽然是公共边,但不是对应边.
3.证明:
∵
AB⊥BC,AD⊥DC,
∴
∠
B=∠D=90
°.
在△ABC和△ADC中,
∠1=∠2
(已知),
∠
B=∠D(已证),
AC=AC
(公共边),
∴
△ABC≌△ADC(AAS),
∴AB=AD.
(1)∵BD⊥m,CE⊥m,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE.
在△BDA和△AEC中,
∵
∴△BDA≌△AEC(AAS);
∵△BDA≌△AEC,
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
1
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
