高中物理新教材人教版必修第一册 自测题 4.5 牛顿运动定律的应用 Word版含解析
文档属性
| 名称 | 高中物理新教材人教版必修第一册 自测题 4.5 牛顿运动定律的应用 Word版含解析 |
|
|
| 格式 | docx | ||
| 文件大小 | 204.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览


文档简介
第四章 运动和力的关系
5 牛顿运动定律的应用
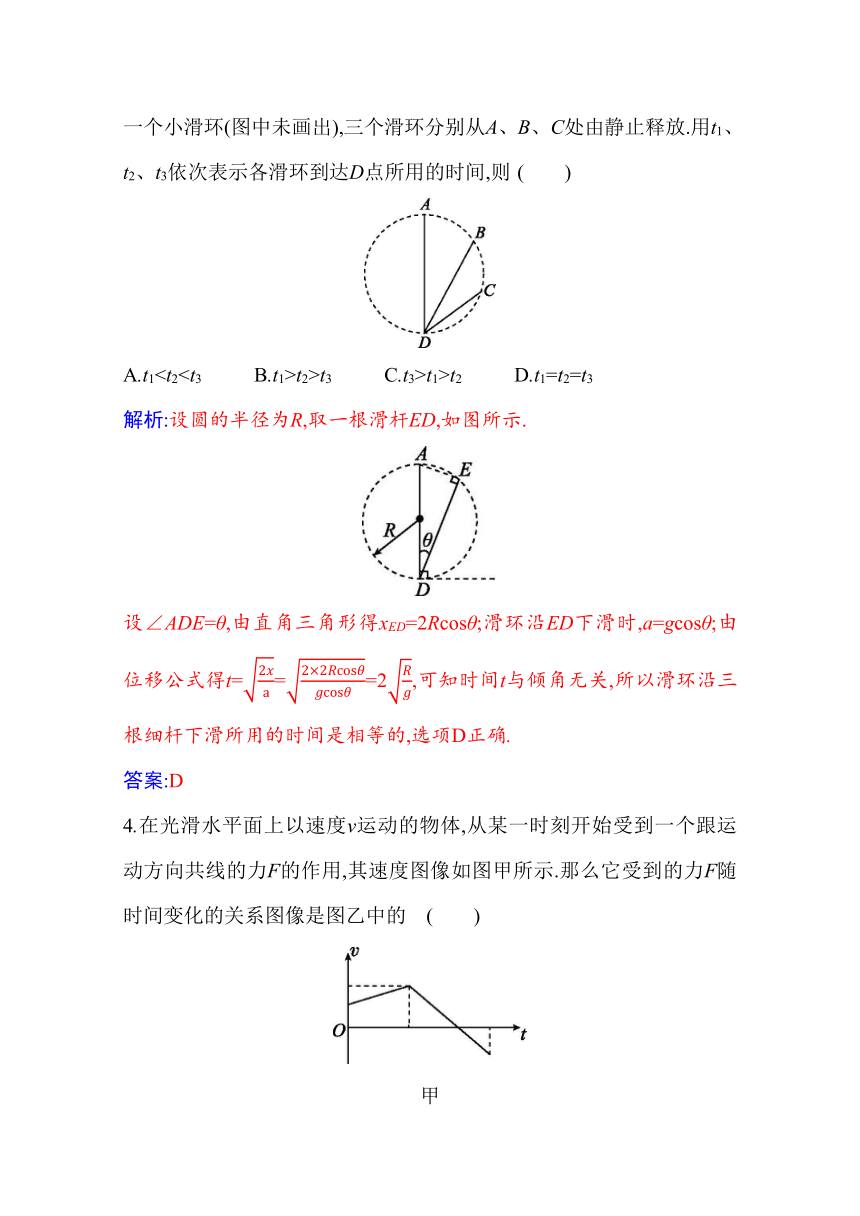
1.一个原来静止在光滑平面上的物体,质量是7 kg,在14 N 的恒力作用下开始沿直线运动,则该物体5 s末的速度大小及5 s内通过的位移大小分别为
( )
A.8 m/s 25 m B.2 m/s 25 m
C.10 m/s 25 m D.10 m/s 12.5 m
答案:C
2.如图甲所示,小物块从足够长的光滑斜面顶端由静止自由滑下.下滑位移为x时的速度为v,其x-v2图像如图乙所示,g取10 m/s2,则斜面倾角θ为
( )
甲 乙
A.30° B.45° C.60° D.75°
答案:A
3.如图所示,AD、BD、CD是竖直平面内三根固定的光滑细杆,A、B、C、D位于同一圆周上,A点为圆周的最高点,D点为最低点.每根杆上都套着一个小滑环(图中未画出),三个滑环分别从A、B、C处由静止释放.用t1、t2、t3依次表示各滑环到达D点所用的时间,则 ( )
A.t1t2>t3 C.t3>t1>t2 D.t1=t2=t3
解析:设圆的半径为R,取一根滑杆ED,如图所示.
设∠ADE=θ,由直角三角形得xED=2Rcosθ;滑环沿ED下滑时,a=gcosθ;由位移公式得t=2xa=2×2Rcosθgcosθ=2Rg,可知时间t与倾角无关,所以滑环沿三根细杆下滑所用的时间是相等的,选项D正确.
答案:D
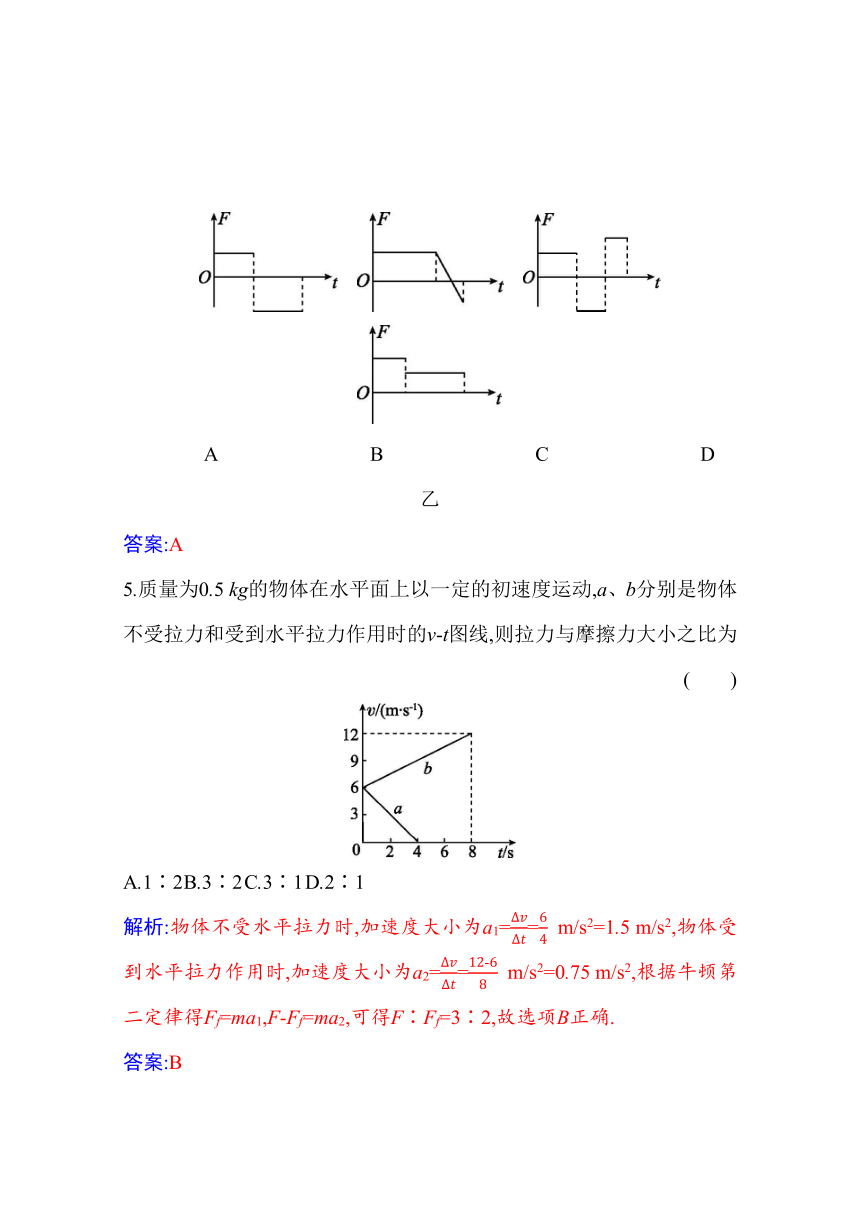
4.在光滑水平面上以速度v运动的物体,从某一时刻开始受到一个跟运动方向共线的力F的作用,其速度图像如图甲所示.那么它受到的力F随时间变化的关系图像是图乙中的 ( )
甲
A B C D
乙
答案:A
5.质量为0.5 kg的物体在水平面上以一定的初速度运动,a、b分别是物体不受拉力和受到水平拉力作用时的v-t图线,则拉力与摩擦力大小之比为
( )
A.1∶2 B.3∶2 C.3∶1 D.2∶1
解析:物体不受水平拉力时,加速度大小为a1=ΔvΔt=64 m/s2=1.5 m/s2,物体受到水平拉力作用时,加速度大小为a2=ΔvΔt=12-68 m/s2=0.75 m/s2,根据牛顿第二定律得Ff=ma1,F-Ff=ma2,可得F∶Ff=3∶2,故选项B正确.
答案:B
6.一架质量m=5.0×103 kg的喷气式飞机,从静止开始在跑道上滑行,经过距离x=5.0×102 m,达到起飞速度v=60 m/s.在这个过程中飞机受到的平均阻力是飞机重力的2%.g取10 m/s2,飞机滑行时受到的牵引力多大?
解析:飞机在加速过程中,由运动学公式得
v2=2ax,
所以a=v22x=3.6 m/s2.
由牛顿第二定律得
F-0.02mg=ma,
所以F=0.02mg+ma=1.9×104 N.
答案:1.9×104 N
【拓展提高】
7.(多选)如图所示,水平传送带以恒定速度v向右运动.将质量为m的物体Q无初速度地放在水平传送带的左端A处,经过t时间后,Q的速度也变为v;再经t时间,物体Q到达传送带的右端B处,则 ( )
A.前t时间内物体Q做匀加速运动,后t时间内物体Q做匀减速运动
B.后t时间内物体Q与传送带之间无摩擦力
C.前t时间内物体Q的位移与后t时间内物体Q的位移大小之比为1∶2
D.物体Q由传送带左端运动到右端相对传送带的位移大小为vt2
解析:前t时间内物体Q受到滑动摩擦力作用,做匀加速直线运动,后t时间内物体Q与传送带间没有摩擦力,做匀速直线运动,选项A错误,选项B正确;前t时间内的位移x1=vt2,后t时间内的位移x2=vt,位移之比为1∶2,选项C正确;物体Q在前t时间内与传送带存在相对运动,Δx=x带-x1=vt2,选项D正确.
答案:BCD
8.(多选)如图所示,一倾角θ=37°的足够长斜面固定在水平地面上.当t=0时,一滑块以初速度v0=10 m/s沿斜面向上运动.已知滑块与斜面间的动摩擦因数μ=0.5,g取10 m/s2,sin 37°=0.6,cos 37°=0.8,下列说法正确的是 ( )
A.滑块一直做匀变速直线运动
B.t=1 s时,滑块速度减为0,然后沿斜面向下运动
C.t=2 s时,滑块恰好又回到出发点
D.t=3 s时,滑块的速度大小为4 m/s
解析:设滑块上滑时的加速度大小为a1,由牛顿第二定律可得mgsinθ+μmgcos θ=ma1,解得a1=10 m/s2,上滑时间t1=v0a1=1 s,上滑的距离x1=12v0t1=5 m,因为mgsinθ>μmgcosθ,滑块速度减小为0后,滑块沿斜面向下运动,选项B正确;设滑块下滑时的加速度大小为a2,由牛顿第二定律得mgsinθ-μmgcosθ=ma2,
解得a2=2 m/s2,经1 s,滑块下滑的距离x2=12a2t22=
1 m<5 m,滑块未回到出发点,选项C错误;因上滑和下滑过程中的加速度不同,故滑块全程不是匀变速直线运动,选项A错误;t=3 s时,滑块沿斜面向下运动,此时的速度v=a2(t-t1)=4 m/s,选项D正确.
答案:BD
9.如图所示,质量m=2 kg的物体静止在水平地面的A处,A、B间距l=20 m,用大小为30 N、沿水平方向的力F拉此物体,经t0=2 s拉至B处.cos 37°=0.8,
sin 37°=0.6,g取10 m/s2.
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30 N,与水平方向成37°的力F'斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t.
解析:(1)物体做匀加速运动,
l=12a0t02,
所以a0=2lt02=2×2022 m/s2=10 m/s2;
由牛顿第二定律F-Ff=ma0,
Ff=30 N-2×10 N=10 N,
所以μ=Ffmg=102×10=0.5.
(2)设F'作用的最短时间为t,物体先以大小为a的加速度匀加速运动时间t,撤去F'后,以大小为a'的加速度匀减速运动时间t'到达B处,速度恰为0.
由牛顿第二定律有
F'cos 37°-μ(mg-F'sin 37°)=ma,
所以a=F'(cos 37°+μsin 37°)m-μg=11.5 m/s2.
a'=Ffm=μg=5 m/s2.
由于匀加速阶段的末速度即为匀减速阶段的初速度,因此有at=a't',
l=12at2+12a't'2,
t=1.03 s.
答案:(1)0.5 (2)1.03 s
【挑战创新】
10.如图所示,螺旋管道内径均匀,内壁光滑,螺距均为d=0.1 m,共5匝,螺旋横截面的半径R=0.2 m,半径R比管道内径大得多,一小球自管道A端从静止开始下滑,求它到达管道B端时的速度大小和所用的时间.
解析:采用整体转化,将螺旋管展开则变成了一倾斜放置的直线管道,小球由沿螺旋线运动变成了沿斜面下滑的匀加速直线运动,如图所示.
在小球下滑过程中,a=gsin θ,
AB总长为10πR,v0=0,
sin θ=5d10πR,
所以v=2ax=2gsinθ·10πR=10 m/s,
t=va=4 s.
答案:10 m/s 4 s
5 牛顿运动定律的应用
1.一个原来静止在光滑平面上的物体,质量是7 kg,在14 N 的恒力作用下开始沿直线运动,则该物体5 s末的速度大小及5 s内通过的位移大小分别为
( )
A.8 m/s 25 m B.2 m/s 25 m
C.10 m/s 25 m D.10 m/s 12.5 m
答案:C
2.如图甲所示,小物块从足够长的光滑斜面顶端由静止自由滑下.下滑位移为x时的速度为v,其x-v2图像如图乙所示,g取10 m/s2,则斜面倾角θ为
( )
甲 乙
A.30° B.45° C.60° D.75°
答案:A
3.如图所示,AD、BD、CD是竖直平面内三根固定的光滑细杆,A、B、C、D位于同一圆周上,A点为圆周的最高点,D点为最低点.每根杆上都套着一个小滑环(图中未画出),三个滑环分别从A、B、C处由静止释放.用t1、t2、t3依次表示各滑环到达D点所用的时间,则 ( )
A.t1
解析:设圆的半径为R,取一根滑杆ED,如图所示.
设∠ADE=θ,由直角三角形得xED=2Rcosθ;滑环沿ED下滑时,a=gcosθ;由位移公式得t=2xa=2×2Rcosθgcosθ=2Rg,可知时间t与倾角无关,所以滑环沿三根细杆下滑所用的时间是相等的,选项D正确.
答案:D
4.在光滑水平面上以速度v运动的物体,从某一时刻开始受到一个跟运动方向共线的力F的作用,其速度图像如图甲所示.那么它受到的力F随时间变化的关系图像是图乙中的 ( )
甲
A B C D
乙
答案:A
5.质量为0.5 kg的物体在水平面上以一定的初速度运动,a、b分别是物体不受拉力和受到水平拉力作用时的v-t图线,则拉力与摩擦力大小之比为
( )
A.1∶2 B.3∶2 C.3∶1 D.2∶1
解析:物体不受水平拉力时,加速度大小为a1=ΔvΔt=64 m/s2=1.5 m/s2,物体受到水平拉力作用时,加速度大小为a2=ΔvΔt=12-68 m/s2=0.75 m/s2,根据牛顿第二定律得Ff=ma1,F-Ff=ma2,可得F∶Ff=3∶2,故选项B正确.
答案:B
6.一架质量m=5.0×103 kg的喷气式飞机,从静止开始在跑道上滑行,经过距离x=5.0×102 m,达到起飞速度v=60 m/s.在这个过程中飞机受到的平均阻力是飞机重力的2%.g取10 m/s2,飞机滑行时受到的牵引力多大?
解析:飞机在加速过程中,由运动学公式得
v2=2ax,
所以a=v22x=3.6 m/s2.
由牛顿第二定律得
F-0.02mg=ma,
所以F=0.02mg+ma=1.9×104 N.
答案:1.9×104 N
【拓展提高】
7.(多选)如图所示,水平传送带以恒定速度v向右运动.将质量为m的物体Q无初速度地放在水平传送带的左端A处,经过t时间后,Q的速度也变为v;再经t时间,物体Q到达传送带的右端B处,则 ( )
A.前t时间内物体Q做匀加速运动,后t时间内物体Q做匀减速运动
B.后t时间内物体Q与传送带之间无摩擦力
C.前t时间内物体Q的位移与后t时间内物体Q的位移大小之比为1∶2
D.物体Q由传送带左端运动到右端相对传送带的位移大小为vt2
解析:前t时间内物体Q受到滑动摩擦力作用,做匀加速直线运动,后t时间内物体Q与传送带间没有摩擦力,做匀速直线运动,选项A错误,选项B正确;前t时间内的位移x1=vt2,后t时间内的位移x2=vt,位移之比为1∶2,选项C正确;物体Q在前t时间内与传送带存在相对运动,Δx=x带-x1=vt2,选项D正确.
答案:BCD
8.(多选)如图所示,一倾角θ=37°的足够长斜面固定在水平地面上.当t=0时,一滑块以初速度v0=10 m/s沿斜面向上运动.已知滑块与斜面间的动摩擦因数μ=0.5,g取10 m/s2,sin 37°=0.6,cos 37°=0.8,下列说法正确的是 ( )
A.滑块一直做匀变速直线运动
B.t=1 s时,滑块速度减为0,然后沿斜面向下运动
C.t=2 s时,滑块恰好又回到出发点
D.t=3 s时,滑块的速度大小为4 m/s
解析:设滑块上滑时的加速度大小为a1,由牛顿第二定律可得mgsinθ+μmgcos θ=ma1,解得a1=10 m/s2,上滑时间t1=v0a1=1 s,上滑的距离x1=12v0t1=5 m,因为mgsinθ>μmgcosθ,滑块速度减小为0后,滑块沿斜面向下运动,选项B正确;设滑块下滑时的加速度大小为a2,由牛顿第二定律得mgsinθ-μmgcosθ=ma2,
解得a2=2 m/s2,经1 s,滑块下滑的距离x2=12a2t22=
1 m<5 m,滑块未回到出发点,选项C错误;因上滑和下滑过程中的加速度不同,故滑块全程不是匀变速直线运动,选项A错误;t=3 s时,滑块沿斜面向下运动,此时的速度v=a2(t-t1)=4 m/s,选项D正确.
答案:BD
9.如图所示,质量m=2 kg的物体静止在水平地面的A处,A、B间距l=20 m,用大小为30 N、沿水平方向的力F拉此物体,经t0=2 s拉至B处.cos 37°=0.8,
sin 37°=0.6,g取10 m/s2.
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30 N,与水平方向成37°的力F'斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t.
解析:(1)物体做匀加速运动,
l=12a0t02,
所以a0=2lt02=2×2022 m/s2=10 m/s2;
由牛顿第二定律F-Ff=ma0,
Ff=30 N-2×10 N=10 N,
所以μ=Ffmg=102×10=0.5.
(2)设F'作用的最短时间为t,物体先以大小为a的加速度匀加速运动时间t,撤去F'后,以大小为a'的加速度匀减速运动时间t'到达B处,速度恰为0.
由牛顿第二定律有
F'cos 37°-μ(mg-F'sin 37°)=ma,
所以a=F'(cos 37°+μsin 37°)m-μg=11.5 m/s2.
a'=Ffm=μg=5 m/s2.
由于匀加速阶段的末速度即为匀减速阶段的初速度,因此有at=a't',
l=12at2+12a't'2,
t=1.03 s.
答案:(1)0.5 (2)1.03 s
【挑战创新】
10.如图所示,螺旋管道内径均匀,内壁光滑,螺距均为d=0.1 m,共5匝,螺旋横截面的半径R=0.2 m,半径R比管道内径大得多,一小球自管道A端从静止开始下滑,求它到达管道B端时的速度大小和所用的时间.
解析:采用整体转化,将螺旋管展开则变成了一倾斜放置的直线管道,小球由沿螺旋线运动变成了沿斜面下滑的匀加速直线运动,如图所示.
在小球下滑过程中,a=gsin θ,
AB总长为10πR,v0=0,
sin θ=5d10πR,
所以v=2ax=2gsinθ·10πR=10 m/s,
t=va=4 s.
答案:10 m/s 4 s
