北师大版七年级上册数学 综合与实践 1.探寻神奇的幻方 课件(27张)
文档属性
| 名称 | 北师大版七年级上册数学 综合与实践 1.探寻神奇的幻方 课件(27张) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 16:21:07 | ||
图片预览





文档简介
综合与实践一
数学北师大版七年级上册
1.通过小组合作学习,探索三阶幻方的基本规律。
学习目标
2.利用三阶幻方的基本规律构造简单的三阶幻方。
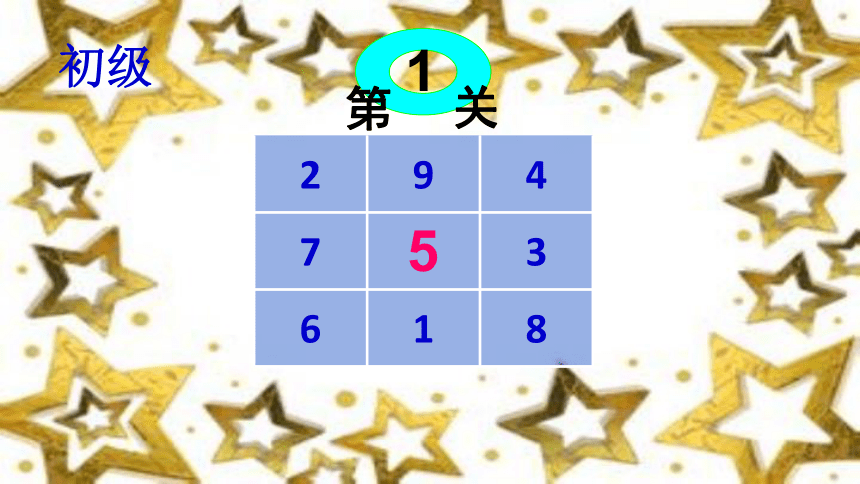
数字游戏
规则:
在空格处填上合适的数,使各行、各列、各对角线上的所有数字的和相等。
初级
中级
高级
2
9
4
7
3
6
1
8
1
第
关
初级
5
6
7
2
1
9
8
4
5
3
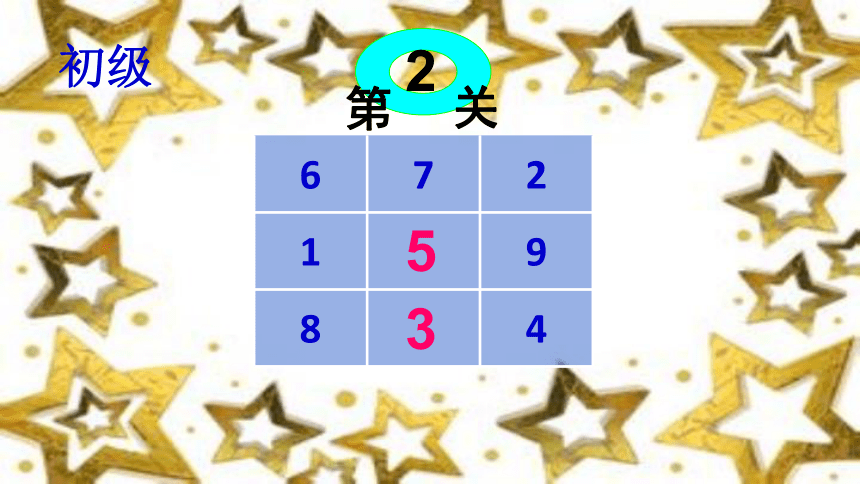
初级
2
第
关
6
8
7
2
9
4
1
5
3
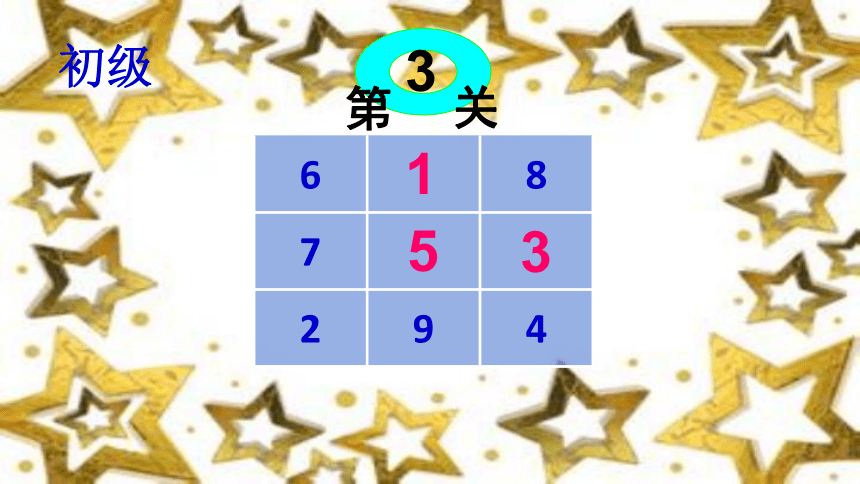
初级
3
第
关
3
8
5
1
2
6
7
9
4
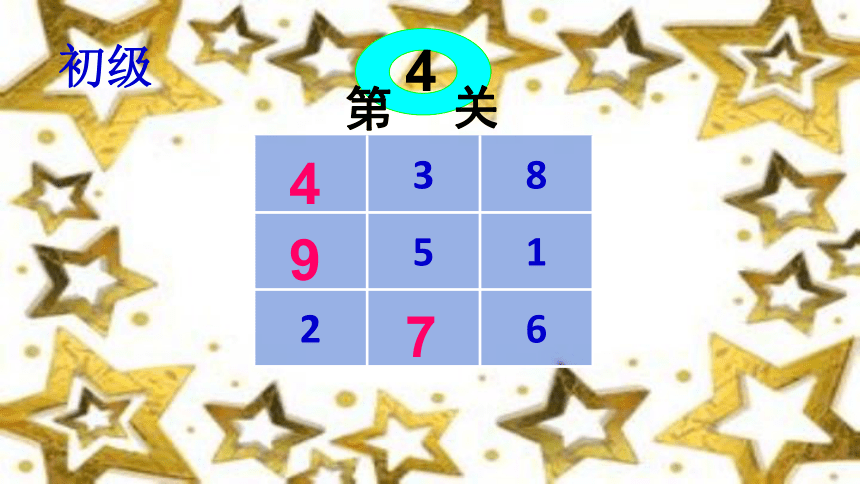
初级
4
第
关
每行、每列、每条对角线上的几个数字的和都相等的方格,叫“幻方”。
每行、每列或每条对角线上的几个数字的和叫“幻和”。
学习目标
1.这些三阶幻方的幻和各是多少?请举例说明。
观察并思考:
2
9
4
7
5
3
6
1
8
6
7
2
1
5
9
8
3
4
6
1
8
7
5
3
2
9
4
4
3
8
9
5
1
2
7
6
2.这些三阶幻方中哪些位置上的数字始终不变?
观察并思考:
中心数
中心数与其他位置上的数字有什么关系?
a
b
c
d
e
f
g
h
i
设幻和为m,则:
a+e+i+b+e+h+c+e+g=3m
(a+b+c)+(i+h+g)+3e=3m
m+m+3e=3m
3e=m
e= m
中心数是幻和的
探寻规律
3.请仔细观察这四个幻方之间能否相互转化?
观察并思考:
2
7
6
9
5
1
4
3
8
8
4
3
9
2
7
1
6
5
4
2
9
7
6
1
3
8
5
2
6
7
1
8
3
9
4
5
6
8
1
3
4
9
7
2
5
8
6
1
7
2
9
3
4
5
4
8
3
1
6
7
9
2
5
2
4
9
3
8
1
7
6
5
6
2
7
9
4
3
1
8
5
①
③
⑤
⑦
②
④
⑥
⑧
旋转的研究方法
探寻规律
10
3
6
8
7
5
4
9
2
幻方中每一个数字都加同一个数,所得方格仍是幻方.
中级
4
9
2
3
5
7
8
1
6
1
第
关
挑战自我
2
0
6
4
3
7
-1
1
5
幻方中每一个数字都减同一个数,所得方格仍是幻方.
2
第
关
中级
4
9
2
3
5
7
8
1
6
挑战自我
3
第
关
8
4
10
2
12
16
18
6
14
幻方中每一个数字都乘同一个不为零的数,所得方格仍是幻方.
4
9
2
3
5
7
8
1
6
中级
挑战自我
请你用1,4,7,10,13,16,19,22,25这九个数设计一个三阶幻方。
10
4
16
22
7
19
25
1
二四为肩
六八为足
左三右七
戴九履一
五居中央
13
高级
1
第
关
挑战自我
请你设计一个幻和为60的三阶幻方。
高级
2
第
关
挑战自我
4+15
9+15
2+15
3+15
20
7+15
8+15
1+15
6+15
请你设计一个幻和为60的三阶幻方。
4×4
9×4
2×4
3×4
20
7×4
8×4
1×4
6×4
高级
2
第
关
挑战自我
总结收获:
一、幻方的智力开发功能。
围棋盘是一个19阶方阵,象棋盘是一个八阶方阵(其将帅宫是一个三阶方阵), 它们的走法原理均同幻方的布局原理相关。
电脑上的“挖地雷”游戏,同九宫图密切相关。
二、幻方对科学的启迪。
美国自动控制论的发明人是通过研究中国的“三三迷宫图”(三阶幻方的联线图)突发奇想。
爱因斯坦的<相对论>,运用了11个公式推算时空相对增减元数,而河洛数对他很有启发。
河南傅熙如运用洛书研究哥德巴赫猜想。
自动化设备控制系统
自动化控制装置
三、幻方应用于科学技术之中。
幻方已应用于“建路”,“爵当曲线”,“七座桥”等的位置解析学及组合解析学中。
七座桥
台湾电机专家吴隆生创造了64阶方阵仪可用于计算机、测量仪、通讯交换仪以及水电、火力、航空等的管制系统。
幻方网站与博客
1.中国幻方 (幻方学会主席的博客)
2.幻立方博客
3.幻环研究博客
4.广州市幻方数棋科技网站---玩数棋
5.陈钦梧幻方世界
6.沈文基幻方研究主页
你可以百度搜索“数独游戏”感受数字游戏的乐趣。
如果你已经被“数字游戏”吸引
如果你已经被“幻方知识”吸引,你可以
变化的是形式
不变的是规律
以不变应万变
就是数学奥秘
洛书故事
公元前三千多年,有条洛河经常发大水,皇帝夏禹带领百姓去治理洛河,这时,从水中浮起一只大乌龟,背上有奇特的图案.
4
2
9
7
5
3
6
1
8
九宫之义
法以灵龟
二四为肩
六八为足
左三右七
戴九履一
五居中央
数学北师大版七年级上册
1.通过小组合作学习,探索三阶幻方的基本规律。
学习目标
2.利用三阶幻方的基本规律构造简单的三阶幻方。
数字游戏
规则:
在空格处填上合适的数,使各行、各列、各对角线上的所有数字的和相等。
初级
中级
高级
2
9
4
7
3
6
1
8
1
第
关
初级
5
6
7
2
1
9
8
4
5
3
初级
2
第
关
6
8
7
2
9
4
1
5
3
初级
3
第
关
3
8
5
1
2
6
7
9
4
初级
4
第
关
每行、每列、每条对角线上的几个数字的和都相等的方格,叫“幻方”。
每行、每列或每条对角线上的几个数字的和叫“幻和”。
学习目标
1.这些三阶幻方的幻和各是多少?请举例说明。
观察并思考:
2
9
4
7
5
3
6
1
8
6
7
2
1
5
9
8
3
4
6
1
8
7
5
3
2
9
4
4
3
8
9
5
1
2
7
6
2.这些三阶幻方中哪些位置上的数字始终不变?
观察并思考:
中心数
中心数与其他位置上的数字有什么关系?
a
b
c
d
e
f
g
h
i
设幻和为m,则:
a+e+i+b+e+h+c+e+g=3m
(a+b+c)+(i+h+g)+3e=3m
m+m+3e=3m
3e=m
e= m
中心数是幻和的
探寻规律
3.请仔细观察这四个幻方之间能否相互转化?
观察并思考:
2
7
6
9
5
1
4
3
8
8
4
3
9
2
7
1
6
5
4
2
9
7
6
1
3
8
5
2
6
7
1
8
3
9
4
5
6
8
1
3
4
9
7
2
5
8
6
1
7
2
9
3
4
5
4
8
3
1
6
7
9
2
5
2
4
9
3
8
1
7
6
5
6
2
7
9
4
3
1
8
5
①
③
⑤
⑦
②
④
⑥
⑧
旋转的研究方法
探寻规律
10
3
6
8
7
5
4
9
2
幻方中每一个数字都加同一个数,所得方格仍是幻方.
中级
4
9
2
3
5
7
8
1
6
1
第
关
挑战自我
2
0
6
4
3
7
-1
1
5
幻方中每一个数字都减同一个数,所得方格仍是幻方.
2
第
关
中级
4
9
2
3
5
7
8
1
6
挑战自我
3
第
关
8
4
10
2
12
16
18
6
14
幻方中每一个数字都乘同一个不为零的数,所得方格仍是幻方.
4
9
2
3
5
7
8
1
6
中级
挑战自我
请你用1,4,7,10,13,16,19,22,25这九个数设计一个三阶幻方。
10
4
16
22
7
19
25
1
二四为肩
六八为足
左三右七
戴九履一
五居中央
13
高级
1
第
关
挑战自我
请你设计一个幻和为60的三阶幻方。
高级
2
第
关
挑战自我
4+15
9+15
2+15
3+15
20
7+15
8+15
1+15
6+15
请你设计一个幻和为60的三阶幻方。
4×4
9×4
2×4
3×4
20
7×4
8×4
1×4
6×4
高级
2
第
关
挑战自我
总结收获:
一、幻方的智力开发功能。
围棋盘是一个19阶方阵,象棋盘是一个八阶方阵(其将帅宫是一个三阶方阵), 它们的走法原理均同幻方的布局原理相关。
电脑上的“挖地雷”游戏,同九宫图密切相关。
二、幻方对科学的启迪。
美国自动控制论的发明人是通过研究中国的“三三迷宫图”(三阶幻方的联线图)突发奇想。
爱因斯坦的<相对论>,运用了11个公式推算时空相对增减元数,而河洛数对他很有启发。
河南傅熙如运用洛书研究哥德巴赫猜想。
自动化设备控制系统
自动化控制装置
三、幻方应用于科学技术之中。
幻方已应用于“建路”,“爵当曲线”,“七座桥”等的位置解析学及组合解析学中。
七座桥
台湾电机专家吴隆生创造了64阶方阵仪可用于计算机、测量仪、通讯交换仪以及水电、火力、航空等的管制系统。
幻方网站与博客
1.中国幻方 (幻方学会主席的博客)
2.幻立方博客
3.幻环研究博客
4.广州市幻方数棋科技网站---玩数棋
5.陈钦梧幻方世界
6.沈文基幻方研究主页
你可以百度搜索“数独游戏”感受数字游戏的乐趣。
如果你已经被“数字游戏”吸引
如果你已经被“幻方知识”吸引,你可以
变化的是形式
不变的是规律
以不变应万变
就是数学奥秘
洛书故事
公元前三千多年,有条洛河经常发大水,皇帝夏禹带领百姓去治理洛河,这时,从水中浮起一只大乌龟,背上有奇特的图案.
4
2
9
7
5
3
6
1
8
九宫之义
法以灵龟
二四为肩
六八为足
左三右七
戴九履一
五居中央
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
