人教版数学八年级上册12.2.4 三角形全等的判定(四)HL 同步练习(Word版 附答案)
文档属性
| 名称 | 人教版数学八年级上册12.2.4 三角形全等的判定(四)HL 同步练习(Word版 附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 84.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览

文档简介
全等三角形
12.2.4 三角形全等的判定(四)HL
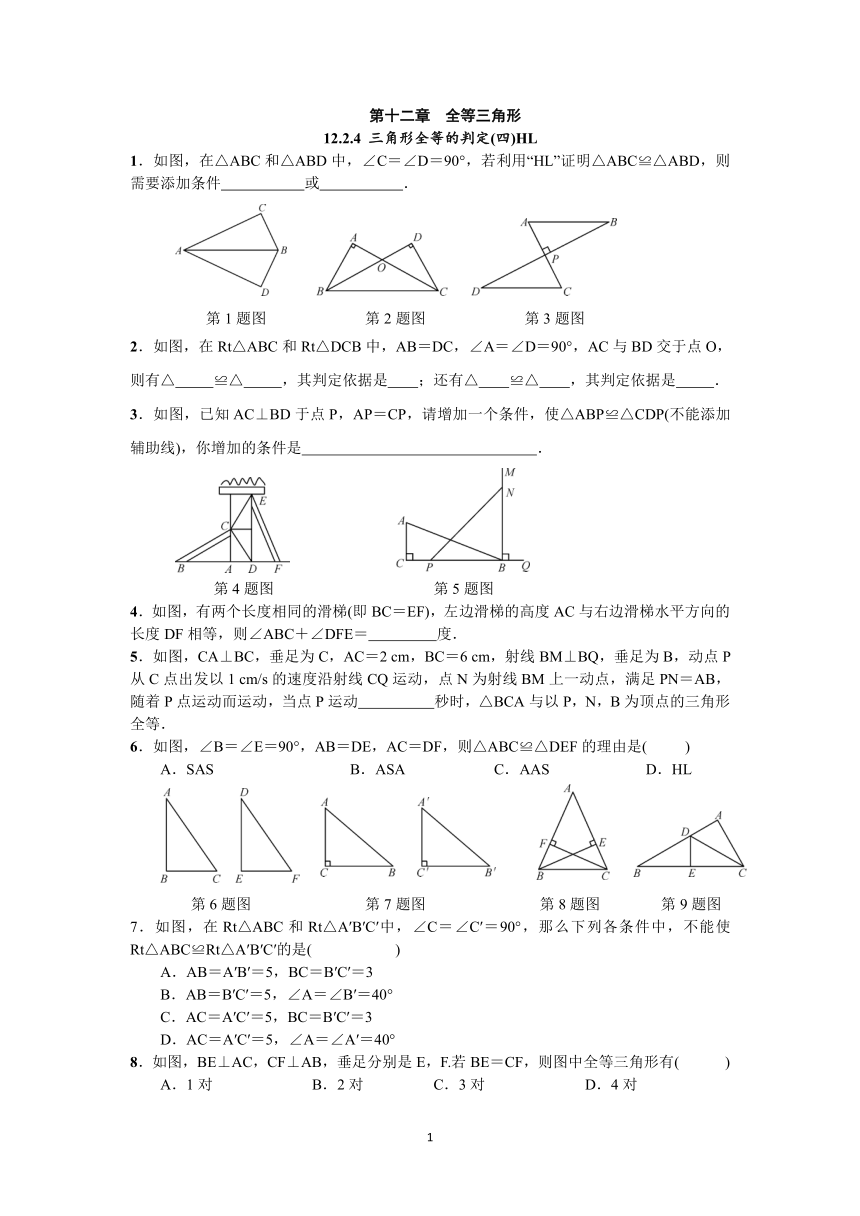
1.如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加条件 或 .
第1题图 第2题图 第3题图
2.如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△ ≌△ ,其判定依据是 ;还有△ ≌△ ,其判定依据是 .
3.如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP(不能添加辅助线),你增加的条件是 .
第4题图 第5题图
4.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度.
5.如图,CA⊥BC,垂足为C,AC=2 cm,BC=6 cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1 cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动 秒时,△BCA与以P,N,B为顶点的三角形全等.
6.如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( )
A.SAS B.ASA C.AAS D.HL
44278552800353573780361951677670152400
第6题图 第7题图 第8题图 第9题图
7.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么下列各条件中,不能使Rt△ABC≌Rt△A′B′C′的是( )
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
8.如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
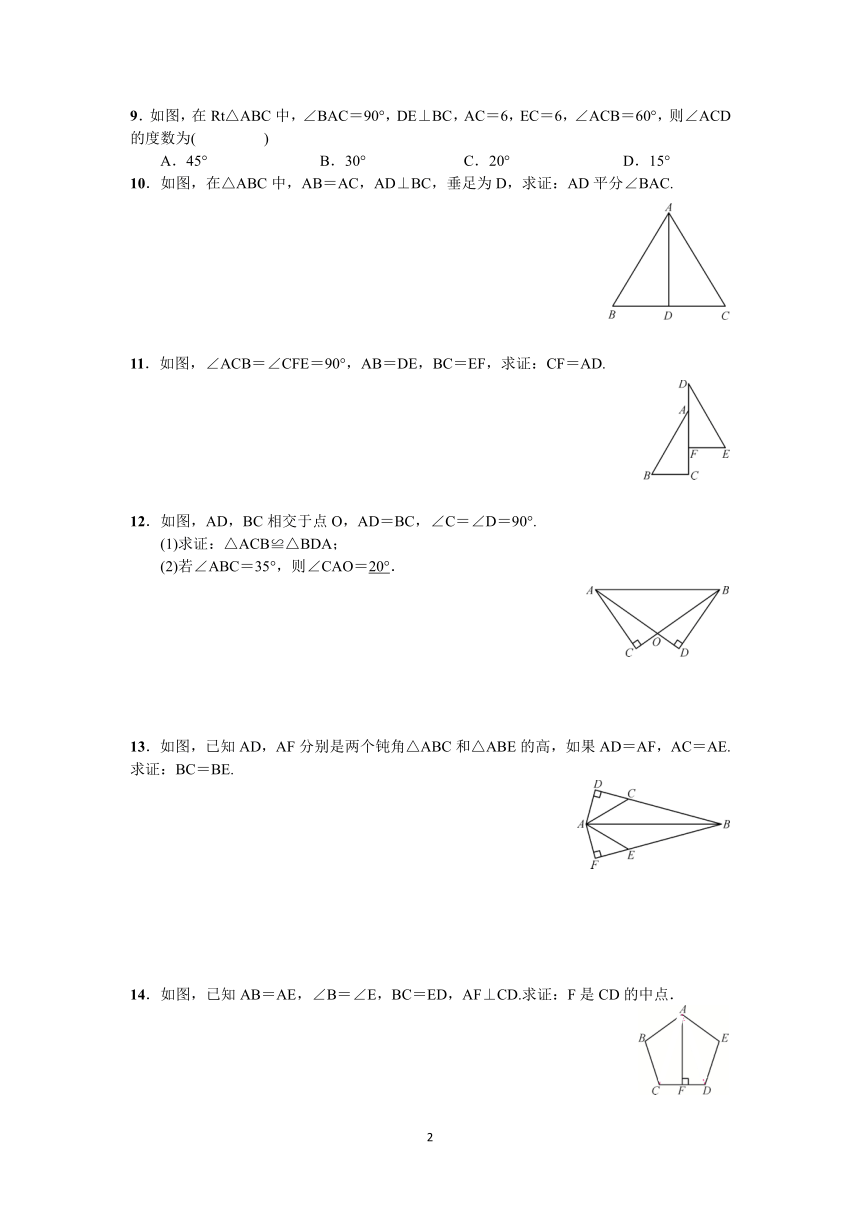
9.如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,AC=6,EC=6,∠ACB=60°,则∠ACD的度数为( )
A.45° B.30° C.20° D.15°
10.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,求证:AD平分∠BAC.
11.如图,∠ACB=∠CFE=90°,AB=DE,BC=EF,求证:CF=AD.
12.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,则∠CAO=20°.
13.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.求证:BC=BE.
14.如图,已知AB=AE,∠B=∠E,BC=ED,AF⊥CD.求证:F是CD的中点.
4881245135255466788589535
参考答案
1.BC=BD AC=AD.
2. ABC △DCB HL; ABO △DCO, AAS.
3.BP=DP或AB=CD或∠A=∠C或∠B=∠D.
4.90.
5.0,4,8,12.
6.D
7.B
8.C
9.B
10.证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,
∴Rt△ABD≌Rt△ACD(HL).
∴∠BAD=∠CAD,即AD平分∠BAC.
11.证明:∵∠ACB=∠CFE=90°,
∴∠ACB=∠DFE=90°.
在Rt△ACB和Rt△DFE中,
∴Rt△ACB≌Rt△DFE(HL).
∴AC=DF.
∴AC-AF=DF-AF,即CF=AD.
12.证明:∵∠C=∠D=90°,
∴△ACB和△BDA是直角三角形.
在Rt△ACB和Rt△BDA中,
∴Rt△ACB≌Rt△BDA(HL).
13.证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,
∴∠ADB=∠AFB=90°.
在Rt△ABD和Rt△ABF中,
∴Rt△ABD≌Rt△ABF(HL).
∴DB=FB.
在Rt△ADC和Rt△AFE中,
∴Rt△ADC≌Rt△AFE(HL).
∴DC=FE.
∴DB-DC=FB-FE,即BC=BE.
14.证明:连接AC,AD.
在△ABC和△AED中,
3060065601980
∴△ABC≌△AED(SAS).
∴AC=AD.
在Rt△ACF和Rt△ADF中,
∴Rt△ACF≌Rt△ADF(HL).
∴CF=DF,
即F为CD的中点.
12.2.4 三角形全等的判定(四)HL
1.如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加条件 或 .
第1题图 第2题图 第3题图
2.如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△ ≌△ ,其判定依据是 ;还有△ ≌△ ,其判定依据是 .
3.如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP(不能添加辅助线),你增加的条件是 .
第4题图 第5题图
4.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度.
5.如图,CA⊥BC,垂足为C,AC=2 cm,BC=6 cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1 cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动 秒时,△BCA与以P,N,B为顶点的三角形全等.
6.如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( )
A.SAS B.ASA C.AAS D.HL
44278552800353573780361951677670152400
第6题图 第7题图 第8题图 第9题图
7.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么下列各条件中,不能使Rt△ABC≌Rt△A′B′C′的是( )
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
8.如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
9.如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,AC=6,EC=6,∠ACB=60°,则∠ACD的度数为( )
A.45° B.30° C.20° D.15°
10.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,求证:AD平分∠BAC.
11.如图,∠ACB=∠CFE=90°,AB=DE,BC=EF,求证:CF=AD.
12.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,则∠CAO=20°.
13.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.求证:BC=BE.
14.如图,已知AB=AE,∠B=∠E,BC=ED,AF⊥CD.求证:F是CD的中点.
4881245135255466788589535
参考答案
1.BC=BD AC=AD.
2. ABC △DCB HL; ABO △DCO, AAS.
3.BP=DP或AB=CD或∠A=∠C或∠B=∠D.
4.90.
5.0,4,8,12.
6.D
7.B
8.C
9.B
10.证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,
∴Rt△ABD≌Rt△ACD(HL).
∴∠BAD=∠CAD,即AD平分∠BAC.
11.证明:∵∠ACB=∠CFE=90°,
∴∠ACB=∠DFE=90°.
在Rt△ACB和Rt△DFE中,
∴Rt△ACB≌Rt△DFE(HL).
∴AC=DF.
∴AC-AF=DF-AF,即CF=AD.
12.证明:∵∠C=∠D=90°,
∴△ACB和△BDA是直角三角形.
在Rt△ACB和Rt△BDA中,
∴Rt△ACB≌Rt△BDA(HL).
13.证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,
∴∠ADB=∠AFB=90°.
在Rt△ABD和Rt△ABF中,
∴Rt△ABD≌Rt△ABF(HL).
∴DB=FB.
在Rt△ADC和Rt△AFE中,
∴Rt△ADC≌Rt△AFE(HL).
∴DC=FE.
∴DB-DC=FB-FE,即BC=BE.
14.证明:连接AC,AD.
在△ABC和△AED中,
3060065601980
∴△ABC≌△AED(SAS).
∴AC=AD.
在Rt△ACF和Rt△ADF中,
∴Rt△ACF≌Rt△ADF(HL).
∴CF=DF,
即F为CD的中点.
