人教版数学九年级上册24.1.4圆周角讲义(表格式 含解析)
文档属性
| 名称 | 人教版数学九年级上册24.1.4圆周角讲义(表格式 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 18:23:52 | ||
图片预览


文档简介
学科教师辅导讲义
学员编号:
年
级:
初三
课
时
数:
3学员姓名:
辅导科目:
数学
学科教师:
授课类型
T同步(圆的角度转换)
授课日期及时段
教学内容
(大脑放电影~)
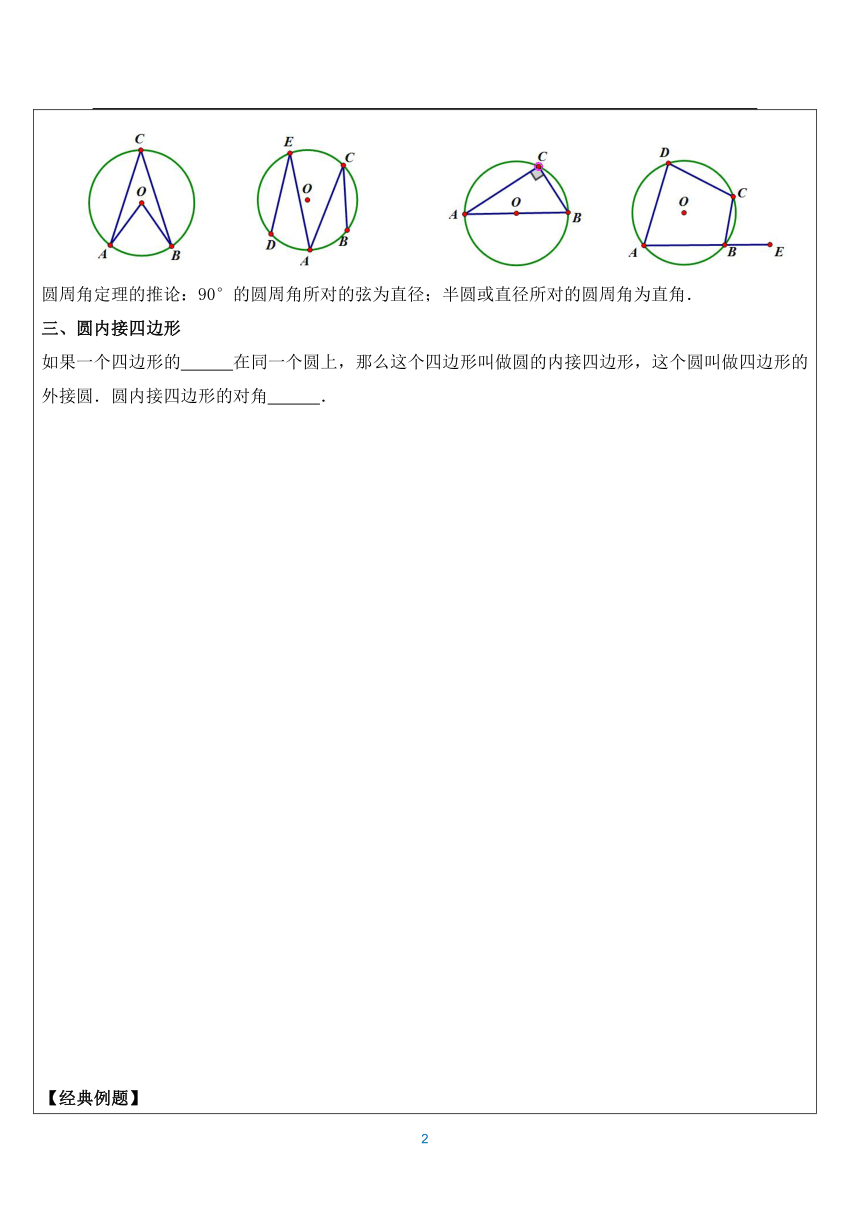
一、与圆有关的角(1)圆心角:顶点在圆心的角叫圆心角。圆心角的性质:圆心角的度数等于它所对的弧的度数。圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角。二、圆心角定理与圆周角定理1.圆心角定理:在同圆或等圆中,同弧所对的圆心角相等。相等的圆心角所对的弧相等
,所对的弦也相等.2.圆心角定理的逆定理:在同圆或等圆中,如果两个
、
、
、
中有一对量相等,那么它们所对应的其余各对量都相等.圆心角所对的弧叫做10的弧,n0的圆心角所对的弧就是n0的弧.2.圆周角定理①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.圆周角定理的推论:90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.三、圆内接四边形如果一个四边形的
在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.圆内接四边形的对角
.【经典例题】知识点一
圆心角与弧的度数之间的转化【例1】如图,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E。求、的度数。【分析】连接CD,由直角三角形的性质求出∠A的度数,再根据等腰三角形及三角形内角和定理分别求出∠ACD及∠DCE的度数,由圆心角、弧、弦的关系即可得出、的度数。【解答】解:连接CD∵△ABC是直角三角形,∠B=36°∴∠A=90°-36°=54°∵AC=DC∴∠ADC=∠A=54°∴∠ACD=180°-∠A-∠ADC=180°-54°-54°=72°∴∠BCD=∠ACB-∠ACD=90°-72°=18°∵∠ACD、∠BCD分别是、所对的圆心角
∴的度数为72°,的度数为18°知识点二
圆周角与圆心角之间的换算【例2】如图,在⊙O中,AB为直径,C,D是⊙O上的两点,CD∥AB,若∠COD=40°,则∠A的度数为__________【分析】由OC=OD,利用等边对等角得到一对角相等,再由两直线平行内错角相等,以及同弧所对的圆周角等于所对圆心角的一半,求出所求即可.【解答】解:∵OC=OD,∠COD=40°∴∠CDO=70°∵AB∥CD∴∠BOD=∠CDO=70°∵∠BOD与∠A都对
∴∠A=∠BOD=35°知识点三
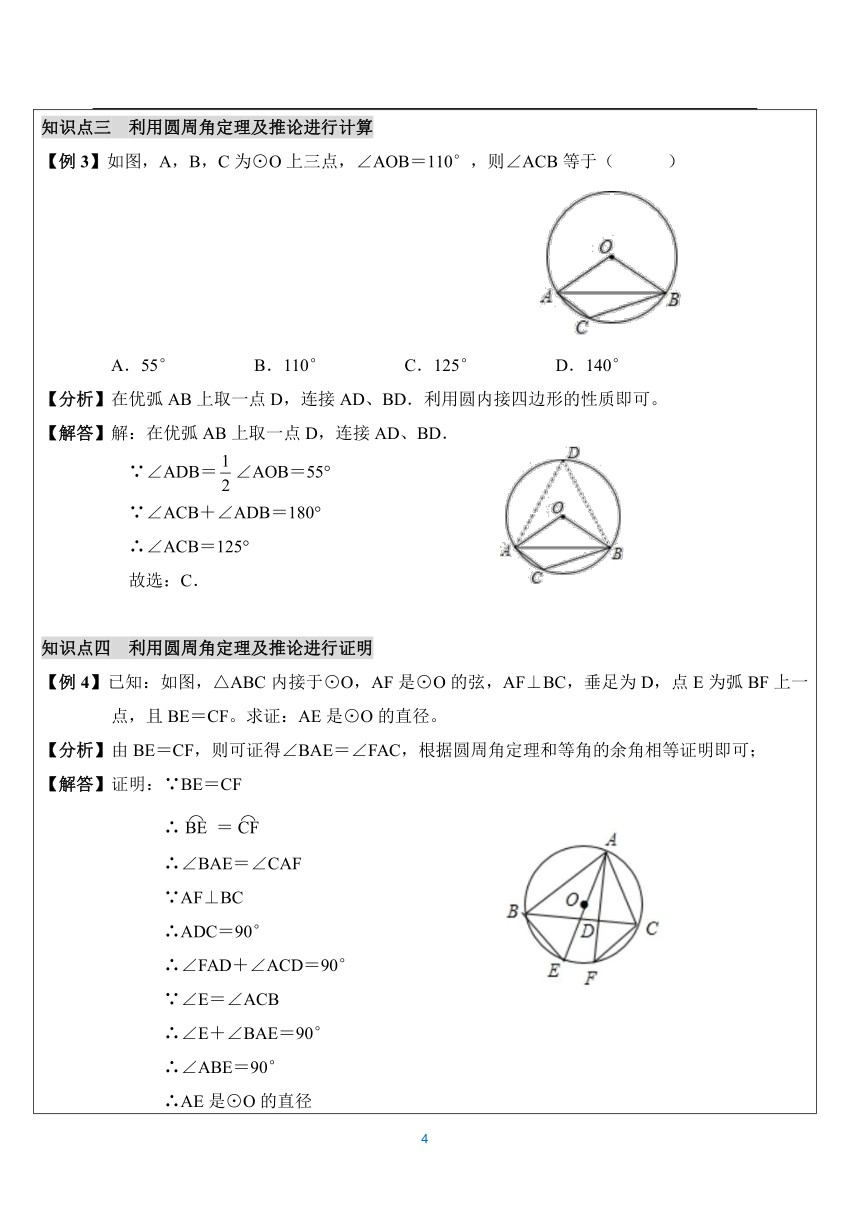
利用圆周角定理及推论进行计算【例3】如图,A,B,C为⊙O上三点,∠AOB=110°,则∠ACB等于(
)A.55°
B.110°
C.125°
D.140°
【分析】在优弧AB上取一点D,连接AD、BD.利用圆内接四边形的性质即可。【解答】解:在优弧AB上取一点D,连接AD、BD.∵∠ADB=∠AOB=55°∵∠ACB+∠ADB=180°∴∠ACB=125°故选:C.知识点四
利用圆周角定理及推论进行证明【例4】已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF。求证:AE是⊙O的直径。【分析】由BE=CF,则可证得∠BAE=∠FAC,根据圆周角定理和等角的余角相等证明即可;【解答】证明:∵BE=CF
∴=
∴∠BAE=∠CAF∵AF⊥BC∴ADC=90°∴∠FAD+∠ACD=90°∵∠E=∠ACB∴∠E+∠BAE=90°∴∠ABE=90°∴AE是⊙O的直径知识点五
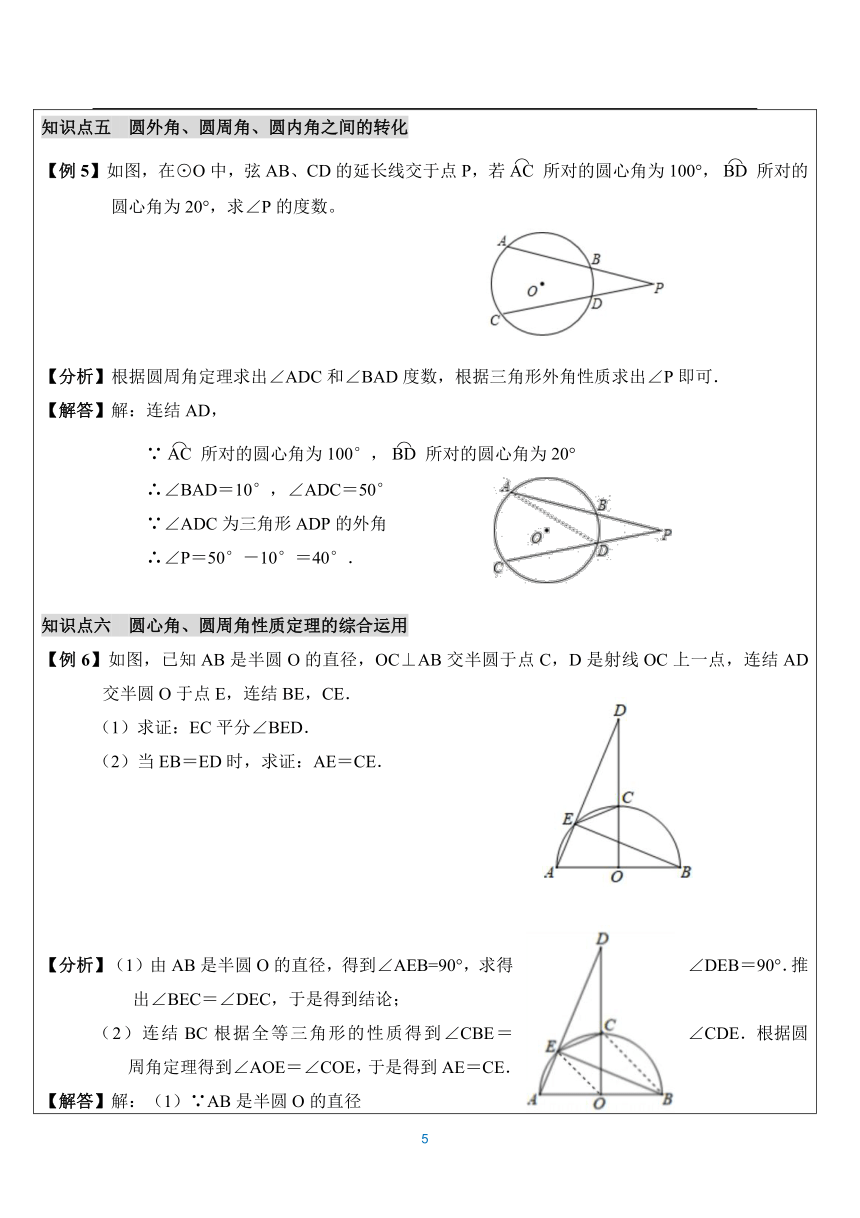
圆外角、圆周角、圆内角之间的转化【例5】如图,在⊙O中,弦AB、CD的延长线交于点P,若所对的圆心角为100°,所对的圆心角为20°,求∠P的度数。【分析】根据圆周角定理求出∠ADC和∠BAD度数,根据三角形外角性质求出∠P即可.【解答】解:连结AD,
∵所对的圆心角为100°,所对的圆心角为20°
∴∠BAD=10°,∠ADC=50°∵∠ADC为三角形ADP的外角∴∠P=50°-10°=40°.知识点六
圆心角、圆周角性质定理的综合运用【例6】如图,已知AB是半圆O的直径,OC⊥AB交半圆于点C,D是射线OC上一点,连结AD交半圆O于点E,连结BE,CE.(1)求证:EC平分∠BED.(2)当EB=ED时,求证:AE=CE.【分析】(1)由AB是半圆O的直径,得到∠AEB=90°,求得∠DEB=90°.推出∠BEC=∠DEC,于是得到结论;(2)连结BC根据全等三角形的性质得到∠CBE=∠CDE.根据圆周角定理得到∠AOE=∠COE,于是得到AE=CE.【解答】解:(1)∵AB是半圆O的直径∴∠AEB=90°∴∠DEB=90°∵OC⊥AB∴∠AOC=∠BOC=90°∴∠BEC=45°∴∠DEC=45°∴∠BEC=∠DEC即EC平分∠BEC;(2)连结BC,OE∵BE=DE,∠BEC=∠DEC,EC=EC
在△BEC与△DEC中
∴△BEC≌△DEC∴∠CBE=∠CDE∵∠CDE=90°-∠A=∠ABE∴∠ABE=∠CBE∴∠AOE=∠COE∴AE=CE.题型一:圆周角与圆心角关系1.如图,A,B,C,D,E是⊙O上的五个点,则图中共有________个圆周角,分别是_____________.【答案】6
∠ACB,∠BCE,∠ACE,∠CBD,∠CED,∠BDE
2.如图,AB是半圆O的直径,C、D是半圆弧上两点,∠D=115°,则∠CAB=( )A.55°
B.45°
C.35°
D.25°【答案】D3.在圆中等于半径的弦所对圆心角的度数是_______,弦所对劣弧所含圆周角的度数是______.【答案】60°
150°
4.在⊙O中,弦AB的长恰好等于半径,求所对的圆周角的大小.【答案】30°5、将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为88°、30°,则∠ACB的大小为( C )A.15°
B.28°
C.29°
D.34°
6.如图,在⊙O中,AB.AC是弦,,求的关系.【答案】7.如图,在⊙O中,弦BC∥OA,AC与OB相交于点D,∠ADB=75°,试求∠C的度数.【答案】∠C=25°.8.如图,已知E是⊙O上任意一点,CD平分∠ACB,求证:ED平分∠AEB.【详解】∵平分,∴,∴∴ED平分∠AEB.题型二:圆内接四边形的性质1.如图,四边形ABCD是⊙O的内接四边形,∠ABC=100°,则∠ADC=( )A.70°
B.80°
C.90°
D.100°【答案】B2.如图,AB是半圆O的直径,C、D是半圆弧上两点,∠D=115°,则∠CAB=( )A.55°
B.45°
C.35°
D.25°【答案】D3、如图,四边形ABCD内接于⊙O,∠DAB=140°,连接OC,点P是半径OC上一点,则∠BPD不可能为( D )A.40°
B.60°
C.80°
D.90°
4.在圆内接四边形ABCD中,若∠A:∠B:∠C=2:3:6,则∠D等于( )A.67.5°
B.135°
C.112.5°
D.45°故选C.5.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )A.45°
B.50°
C.55°
D.60°故选B.6.如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )A.25°
B.30°
C.40°
D.55°故选:C.7.如图,O是线段BC的中点,A、D、C到O点的距离相等,若∠ABC=30°,则∠ADC的度数是( )A.150°
B.120°
C.60°
D.30°故选A8、如图,点O为△ABC内一点,OA=OB=OC,且∠ABO=40°,则∠ACB的大小是( B )A.40°
B.50°
C.60°
D.70°
9.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F,∠E=α,∠F=β,则∠A=( )A.α+β
B.
C.180﹣α﹣β
D.【解答】连结EF,如图,∵四边形ABCD为圆的内接四边形,∴∠ECD=∠A,∵∠ECD=∠1+∠2,∴∠A=∠1+∠2,∵∠A+∠1+∠2+∠E+∠F=180°,∴2∠A+α+β=180°,∴∠A=.故选D.10、如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状,并证明你的结论.(2)证明:PA+PB=PC.11、(2019?马鞍山二模)如图,已知AB是⊙O的直径,弦CD⊥AB于点E,F是上的一点,AF,CD的延长线相交于点G.(1)若⊙O的半径为,且∠DFC=45°,求弦CD的长.(2)求证:∠AFC=∠DFG.12、(2019?临海市一模)如图,点A,B,C在⊙O上,AB∥OC.(1)求证:∠ACB+∠BOC=90°;(2)若⊙O的半径为5,AC=8,求BC的长度.13、(2019春?江都区校级月考)如图,在△ABD中,AB=AD,以AB为直径的圆交AD于点E,交BD于点F,过点D作DC∥AB交AF的延长线于点C,连接CB.(1)求证:四边形ABCD为菱形;(2)若AE=7,BF=2,求半圆的半径和菱形ABCD的面积.14、(2019?阜阳模拟)如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E,连接AD,BC,CO(1)当∠BCO=25°时,求∠A的度数;(2)若CD=,BE=4,求⊙O的半径.【课堂达标检测】1.
如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为(
)A.84°
B.60°
C.36°
D.24°【解答】解:∵∠B与∠C所对的弧都是∴∠C=∠B=24°故选:D2.
如图,点A、B、C都在⊙O上,若∠AOC=140°,则∠B的度数是(
)A.70°
B.80°
C.110°
D.140°
【解答】解:作所对的圆周角∠APC,如图,∵∠P=∠AOC=×140°=70°∵∠P+∠B=180°∴∠B=180°70°=110°故选:C
3.
如图,在⊙O中,点C是的中点,∠A=40°,则∠BOC的大小为(
)
A.40°
B.45°
C.50°
D.60°
【解答】解:∵OA=OB,∠A=40°∴∠B=∠A=40°∴∠AOB=180°-∠A-∠B=100°∵点C是的中点,OC过O
∴=
∴∠BOC=∠AOC=∠AOB=50°故选:C.4.
如图,在⊙O中,已知OA⊥BC,∠AOB=58°,则∠ADC的度数为(
)
A.29°
B.58°
C.87°
D.32°
【解答】解:∵OA⊥BC,∴=
∴∠ADC=∠AOB=29°故选:A5.
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么BC的长是(
)
A.
B.
C.
1
D.
【解答】解:∵∠BAC=60°∴∠BOC=120°∵OD⊥弦BC∴∠BOD=90°∵∠BOD=∠A=60°∴OD=OB=1
∴
∴BC=2BD=
故选:A【培优特训】6.
如图,已知在⊙O中,半径OA=,弦AB=2,∠BAD=18°,OD与AB交于点C,则∠ACO=________度【解答】解:∵OA=
,OB=,AB=2
∴,OA=OB∴△AOB是等腰直角三角形,∠AOB=90°∴∠OBA=45°∵∠BAD=18°∴∠BOD=36°∴∠ACO=∠OBA+∠BOD=45°+36°=81°故答案为:817.
如图,AB、BC是⊙O的弦,OM∥BC交AB于M,若∠AOC=100°,则∠AMO=________°【解答】解:∵∠AOC=2∠B,∠AOC=100°,∴∠B=50°,∵OM∥BC,∴∠AMO=∠B=50°,故答案为:508.
如图,点A、B、C在圆O上,弦AC与半径OB互相平分,则∠ABC=________度.【解答】解:∵弦AC与半径OB互相平分∴OA=AB∵OA=OC∴△OAB是等边三角形∴∠AOB=60°∴∠AOC=120°∴∠ABC=120°故答案为1209.
如图,AB是⊙O的直径,C、D两点在⊙O上,若∠C=45°,(1)求∠ABD的度数;(2)若∠CDB=30°,BC=3,求⊙O的半径。【解答】解:(1)∵∠C=45°∴∠A=∠C=45°∵AB是⊙O的直径∴∠ADB=90°∴∠ABD=45°;(2)连接AC∵AB是⊙O的直径∴∠ACB=90°∵∠CAB=∠CDB=30°,BC=3∴AB=6∴⊙O的半径为310.
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,过点C作CM∥BP交PA的延长线于点M.(1)求证:△ACM≌△BCP;(2)若PA=1,PB=2,求△PCM的面积【解答】证明:∵∠APC=∠CPB=60°∴∠BAC=∠ABC=60°∴△ABC是等边三角形∴BC=AC,∠ACB=60°∵CM∥BP∴∠PCM=∠BPC=60°又∵∠APC=60°∴△PCM是等边三角形∴PC=MC,∠M=60°∵∠BCA-∠PCA=∠PCM-∠PCA∴∠PCB=∠ACM在△ACM和△BCP中
∴△ACM≌△BCP≌△ACM(AAS)
(2)∵△ACM≌△BCP∴AM=PB=2∴PM=PA+AM=1+2=3∵△PCM是等边三角形∴△PCM的面积==【中考链接】11.
(2018?广东)同圆中,已知所对的圆心角是100°,则所对的圆周角是______【解答】解:弧AB所对的圆心角是100°,则弧AB所对的圆周角为50°.故答案为50°.12.
(2018?威海)如图,⊙O的半径为5,AB为弦,点C为的中点,若∠ABC=30°,则弦AB的长为(
)
A.
B.
5
C.
D.
【解答】解:连接OC、OA
∵∠ABC=30°∴∠AOC=60°∵AB为弦,点C为的中点∴OC⊥AB在Rt△OAE中,AE=
∴AB=
故选:D13.(2018?白银)如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是(
)A.15°
B.30°
C.45°
D.60°
【解答】解:连接DC
∵C(,0),D(0,1)∴∠DOC=90°,OD=1,OC=∴∠DCO=30°∴∠OBD=30°故选:B.
T同步——圆的角度转换同步训练
同步知识梳理
1
学员编号:
年
级:
初三
课
时
数:
3学员姓名:
辅导科目:
数学
学科教师:
授课类型
T同步(圆的角度转换)
授课日期及时段
教学内容
(大脑放电影~)
一、与圆有关的角(1)圆心角:顶点在圆心的角叫圆心角。圆心角的性质:圆心角的度数等于它所对的弧的度数。圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角。二、圆心角定理与圆周角定理1.圆心角定理:在同圆或等圆中,同弧所对的圆心角相等。相等的圆心角所对的弧相等
,所对的弦也相等.2.圆心角定理的逆定理:在同圆或等圆中,如果两个
、
、
、
中有一对量相等,那么它们所对应的其余各对量都相等.圆心角所对的弧叫做10的弧,n0的圆心角所对的弧就是n0的弧.2.圆周角定理①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.圆周角定理的推论:90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.三、圆内接四边形如果一个四边形的
在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.圆内接四边形的对角
.【经典例题】知识点一
圆心角与弧的度数之间的转化【例1】如图,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E。求、的度数。【分析】连接CD,由直角三角形的性质求出∠A的度数,再根据等腰三角形及三角形内角和定理分别求出∠ACD及∠DCE的度数,由圆心角、弧、弦的关系即可得出、的度数。【解答】解:连接CD∵△ABC是直角三角形,∠B=36°∴∠A=90°-36°=54°∵AC=DC∴∠ADC=∠A=54°∴∠ACD=180°-∠A-∠ADC=180°-54°-54°=72°∴∠BCD=∠ACB-∠ACD=90°-72°=18°∵∠ACD、∠BCD分别是、所对的圆心角
∴的度数为72°,的度数为18°知识点二
圆周角与圆心角之间的换算【例2】如图,在⊙O中,AB为直径,C,D是⊙O上的两点,CD∥AB,若∠COD=40°,则∠A的度数为__________【分析】由OC=OD,利用等边对等角得到一对角相等,再由两直线平行内错角相等,以及同弧所对的圆周角等于所对圆心角的一半,求出所求即可.【解答】解:∵OC=OD,∠COD=40°∴∠CDO=70°∵AB∥CD∴∠BOD=∠CDO=70°∵∠BOD与∠A都对
∴∠A=∠BOD=35°知识点三
利用圆周角定理及推论进行计算【例3】如图,A,B,C为⊙O上三点,∠AOB=110°,则∠ACB等于(
)A.55°
B.110°
C.125°
D.140°
【分析】在优弧AB上取一点D,连接AD、BD.利用圆内接四边形的性质即可。【解答】解:在优弧AB上取一点D,连接AD、BD.∵∠ADB=∠AOB=55°∵∠ACB+∠ADB=180°∴∠ACB=125°故选:C.知识点四
利用圆周角定理及推论进行证明【例4】已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF。求证:AE是⊙O的直径。【分析】由BE=CF,则可证得∠BAE=∠FAC,根据圆周角定理和等角的余角相等证明即可;【解答】证明:∵BE=CF
∴=
∴∠BAE=∠CAF∵AF⊥BC∴ADC=90°∴∠FAD+∠ACD=90°∵∠E=∠ACB∴∠E+∠BAE=90°∴∠ABE=90°∴AE是⊙O的直径知识点五
圆外角、圆周角、圆内角之间的转化【例5】如图,在⊙O中,弦AB、CD的延长线交于点P,若所对的圆心角为100°,所对的圆心角为20°,求∠P的度数。【分析】根据圆周角定理求出∠ADC和∠BAD度数,根据三角形外角性质求出∠P即可.【解答】解:连结AD,
∵所对的圆心角为100°,所对的圆心角为20°
∴∠BAD=10°,∠ADC=50°∵∠ADC为三角形ADP的外角∴∠P=50°-10°=40°.知识点六
圆心角、圆周角性质定理的综合运用【例6】如图,已知AB是半圆O的直径,OC⊥AB交半圆于点C,D是射线OC上一点,连结AD交半圆O于点E,连结BE,CE.(1)求证:EC平分∠BED.(2)当EB=ED时,求证:AE=CE.【分析】(1)由AB是半圆O的直径,得到∠AEB=90°,求得∠DEB=90°.推出∠BEC=∠DEC,于是得到结论;(2)连结BC根据全等三角形的性质得到∠CBE=∠CDE.根据圆周角定理得到∠AOE=∠COE,于是得到AE=CE.【解答】解:(1)∵AB是半圆O的直径∴∠AEB=90°∴∠DEB=90°∵OC⊥AB∴∠AOC=∠BOC=90°∴∠BEC=45°∴∠DEC=45°∴∠BEC=∠DEC即EC平分∠BEC;(2)连结BC,OE∵BE=DE,∠BEC=∠DEC,EC=EC
在△BEC与△DEC中
∴△BEC≌△DEC∴∠CBE=∠CDE∵∠CDE=90°-∠A=∠ABE∴∠ABE=∠CBE∴∠AOE=∠COE∴AE=CE.题型一:圆周角与圆心角关系1.如图,A,B,C,D,E是⊙O上的五个点,则图中共有________个圆周角,分别是_____________.【答案】6
∠ACB,∠BCE,∠ACE,∠CBD,∠CED,∠BDE
2.如图,AB是半圆O的直径,C、D是半圆弧上两点,∠D=115°,则∠CAB=( )A.55°
B.45°
C.35°
D.25°【答案】D3.在圆中等于半径的弦所对圆心角的度数是_______,弦所对劣弧所含圆周角的度数是______.【答案】60°
150°
4.在⊙O中,弦AB的长恰好等于半径,求所对的圆周角的大小.【答案】30°5、将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为88°、30°,则∠ACB的大小为( C )A.15°
B.28°
C.29°
D.34°
6.如图,在⊙O中,AB.AC是弦,,求的关系.【答案】7.如图,在⊙O中,弦BC∥OA,AC与OB相交于点D,∠ADB=75°,试求∠C的度数.【答案】∠C=25°.8.如图,已知E是⊙O上任意一点,CD平分∠ACB,求证:ED平分∠AEB.【详解】∵平分,∴,∴∴ED平分∠AEB.题型二:圆内接四边形的性质1.如图,四边形ABCD是⊙O的内接四边形,∠ABC=100°,则∠ADC=( )A.70°
B.80°
C.90°
D.100°【答案】B2.如图,AB是半圆O的直径,C、D是半圆弧上两点,∠D=115°,则∠CAB=( )A.55°
B.45°
C.35°
D.25°【答案】D3、如图,四边形ABCD内接于⊙O,∠DAB=140°,连接OC,点P是半径OC上一点,则∠BPD不可能为( D )A.40°
B.60°
C.80°
D.90°
4.在圆内接四边形ABCD中,若∠A:∠B:∠C=2:3:6,则∠D等于( )A.67.5°
B.135°
C.112.5°
D.45°故选C.5.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )A.45°
B.50°
C.55°
D.60°故选B.6.如图,圆内接四边形ABCD的两组对边的延长线分别相较于点E,F,若∠A=55°,∠E=30°,则∠F=( )A.25°
B.30°
C.40°
D.55°故选:C.7.如图,O是线段BC的中点,A、D、C到O点的距离相等,若∠ABC=30°,则∠ADC的度数是( )A.150°
B.120°
C.60°
D.30°故选A8、如图,点O为△ABC内一点,OA=OB=OC,且∠ABO=40°,则∠ACB的大小是( B )A.40°
B.50°
C.60°
D.70°
9.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F,∠E=α,∠F=β,则∠A=( )A.α+β
B.
C.180﹣α﹣β
D.【解答】连结EF,如图,∵四边形ABCD为圆的内接四边形,∴∠ECD=∠A,∵∠ECD=∠1+∠2,∴∠A=∠1+∠2,∵∠A+∠1+∠2+∠E+∠F=180°,∴2∠A+α+β=180°,∴∠A=.故选D.10、如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状,并证明你的结论.(2)证明:PA+PB=PC.11、(2019?马鞍山二模)如图,已知AB是⊙O的直径,弦CD⊥AB于点E,F是上的一点,AF,CD的延长线相交于点G.(1)若⊙O的半径为,且∠DFC=45°,求弦CD的长.(2)求证:∠AFC=∠DFG.12、(2019?临海市一模)如图,点A,B,C在⊙O上,AB∥OC.(1)求证:∠ACB+∠BOC=90°;(2)若⊙O的半径为5,AC=8,求BC的长度.13、(2019春?江都区校级月考)如图,在△ABD中,AB=AD,以AB为直径的圆交AD于点E,交BD于点F,过点D作DC∥AB交AF的延长线于点C,连接CB.(1)求证:四边形ABCD为菱形;(2)若AE=7,BF=2,求半圆的半径和菱形ABCD的面积.14、(2019?阜阳模拟)如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E,连接AD,BC,CO(1)当∠BCO=25°时,求∠A的度数;(2)若CD=,BE=4,求⊙O的半径.【课堂达标检测】1.
如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为(
)A.84°
B.60°
C.36°
D.24°【解答】解:∵∠B与∠C所对的弧都是∴∠C=∠B=24°故选:D2.
如图,点A、B、C都在⊙O上,若∠AOC=140°,则∠B的度数是(
)A.70°
B.80°
C.110°
D.140°
【解答】解:作所对的圆周角∠APC,如图,∵∠P=∠AOC=×140°=70°∵∠P+∠B=180°∴∠B=180°70°=110°故选:C
3.
如图,在⊙O中,点C是的中点,∠A=40°,则∠BOC的大小为(
)
A.40°
B.45°
C.50°
D.60°
【解答】解:∵OA=OB,∠A=40°∴∠B=∠A=40°∴∠AOB=180°-∠A-∠B=100°∵点C是的中点,OC过O
∴=
∴∠BOC=∠AOC=∠AOB=50°故选:C.4.
如图,在⊙O中,已知OA⊥BC,∠AOB=58°,则∠ADC的度数为(
)
A.29°
B.58°
C.87°
D.32°
【解答】解:∵OA⊥BC,∴=
∴∠ADC=∠AOB=29°故选:A5.
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么BC的长是(
)
A.
B.
C.
1
D.
【解答】解:∵∠BAC=60°∴∠BOC=120°∵OD⊥弦BC∴∠BOD=90°∵∠BOD=∠A=60°∴OD=OB=1
∴
∴BC=2BD=
故选:A【培优特训】6.
如图,已知在⊙O中,半径OA=,弦AB=2,∠BAD=18°,OD与AB交于点C,则∠ACO=________度【解答】解:∵OA=
,OB=,AB=2
∴,OA=OB∴△AOB是等腰直角三角形,∠AOB=90°∴∠OBA=45°∵∠BAD=18°∴∠BOD=36°∴∠ACO=∠OBA+∠BOD=45°+36°=81°故答案为:817.
如图,AB、BC是⊙O的弦,OM∥BC交AB于M,若∠AOC=100°,则∠AMO=________°【解答】解:∵∠AOC=2∠B,∠AOC=100°,∴∠B=50°,∵OM∥BC,∴∠AMO=∠B=50°,故答案为:508.
如图,点A、B、C在圆O上,弦AC与半径OB互相平分,则∠ABC=________度.【解答】解:∵弦AC与半径OB互相平分∴OA=AB∵OA=OC∴△OAB是等边三角形∴∠AOB=60°∴∠AOC=120°∴∠ABC=120°故答案为1209.
如图,AB是⊙O的直径,C、D两点在⊙O上,若∠C=45°,(1)求∠ABD的度数;(2)若∠CDB=30°,BC=3,求⊙O的半径。【解答】解:(1)∵∠C=45°∴∠A=∠C=45°∵AB是⊙O的直径∴∠ADB=90°∴∠ABD=45°;(2)连接AC∵AB是⊙O的直径∴∠ACB=90°∵∠CAB=∠CDB=30°,BC=3∴AB=6∴⊙O的半径为310.
如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,过点C作CM∥BP交PA的延长线于点M.(1)求证:△ACM≌△BCP;(2)若PA=1,PB=2,求△PCM的面积【解答】证明:∵∠APC=∠CPB=60°∴∠BAC=∠ABC=60°∴△ABC是等边三角形∴BC=AC,∠ACB=60°∵CM∥BP∴∠PCM=∠BPC=60°又∵∠APC=60°∴△PCM是等边三角形∴PC=MC,∠M=60°∵∠BCA-∠PCA=∠PCM-∠PCA∴∠PCB=∠ACM在△ACM和△BCP中
∴△ACM≌△BCP≌△ACM(AAS)
(2)∵△ACM≌△BCP∴AM=PB=2∴PM=PA+AM=1+2=3∵△PCM是等边三角形∴△PCM的面积==【中考链接】11.
(2018?广东)同圆中,已知所对的圆心角是100°,则所对的圆周角是______【解答】解:弧AB所对的圆心角是100°,则弧AB所对的圆周角为50°.故答案为50°.12.
(2018?威海)如图,⊙O的半径为5,AB为弦,点C为的中点,若∠ABC=30°,则弦AB的长为(
)
A.
B.
5
C.
D.
【解答】解:连接OC、OA
∵∠ABC=30°∴∠AOC=60°∵AB为弦,点C为的中点∴OC⊥AB在Rt△OAE中,AE=
∴AB=
故选:D13.(2018?白银)如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是(
)A.15°
B.30°
C.45°
D.60°
【解答】解:连接DC
∵C(,0),D(0,1)∴∠DOC=90°,OD=1,OC=∴∠DCO=30°∴∠OBD=30°故选:B.
T同步——圆的角度转换同步训练
同步知识梳理
1
同课章节目录
