人教版小学数学小升初冲刺试题 代数
图片预览



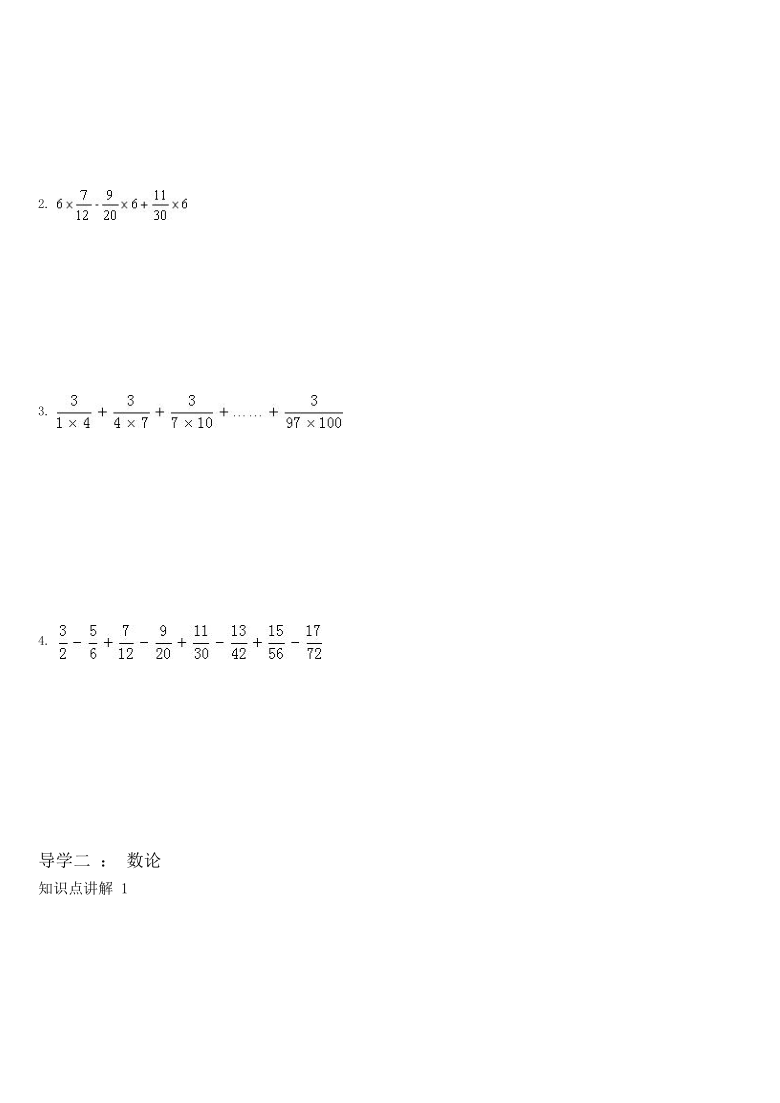
文档简介
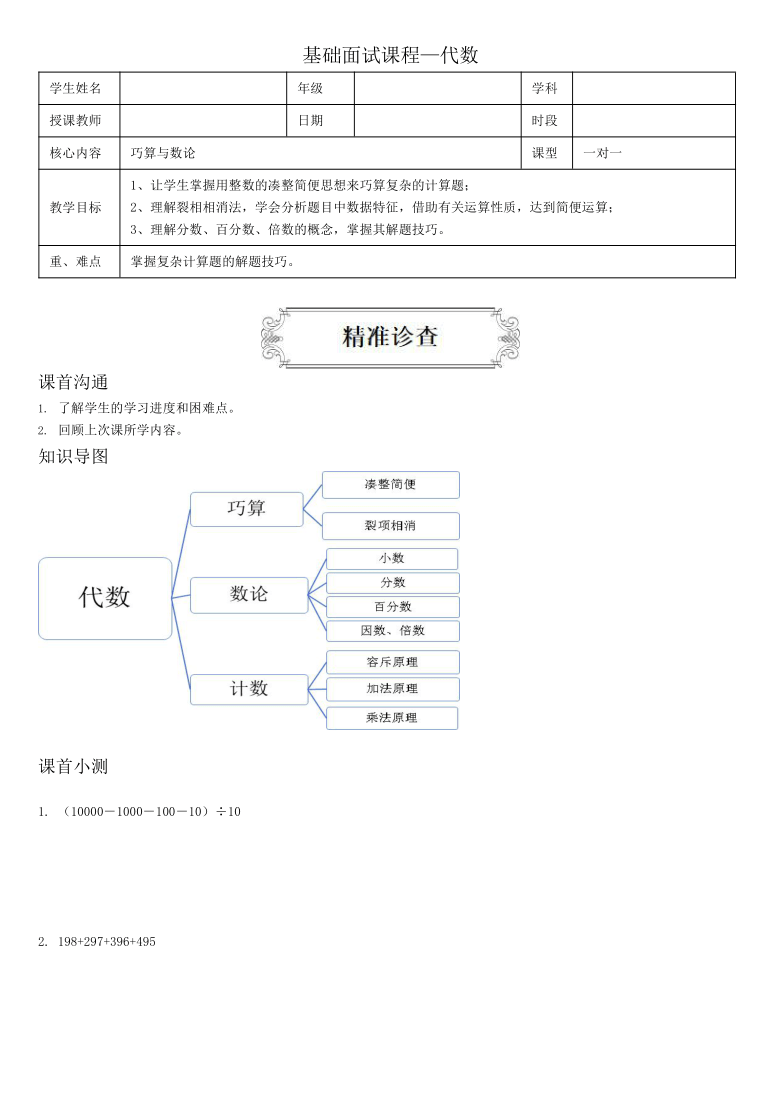
基础面试课程—代数
学生姓名
年级
学科
授课教师
日期
时段
核心内容
巧算与数论
课型
一对一
教学目标
1、让学生掌握用整数的凑整简便思想来巧算复杂的计算题;
2、理解裂相相消法,学会分析题目中数据特征,借助有关运算性质,达到简便运算;
3、理解分数、百分数、倍数的概念,掌握其解题技巧。
重、难点
掌握复杂计算题的解题技巧。
2532380114935
课首沟通
了解学生的学习进度和困难点。
回顾上次课所学内容。
368300321310知识导图
课首小测
1. (10000-1000-100-10)÷10
2. 198+297+396+495
581025-31753.
581025-762004.
581025-577855.
2532380133350
导学一 : 巧算
知识点讲解 1:整数凑整
例 1. (西关外国语面谈考试 )
例 2. (广州某外国语面试数学卷三)125×32=( ) 例 3. 487+(213-92)
例 4. 3333+3333-3333×3333÷3333
我爱展示
1. (广州某外国语面试数学卷三)25×24=( )
2. (广州某外国语面试数学卷四)25+32-2=( )
3. 432―(154―68)=( )
知识点讲解 2:稍复杂数的连加减
例 1. 9+99+999+9999
例 2. 1-2-3+4+5-6……-78-79+80+81
例 3.
我爱展示
1. 99999+9999+999+99+9=( )
2. 9+98+996+9997=(
3. 1999+2998+396+497=(
)
)
4. 487+321+113+479=(
5. 723-251+177=(
)
)
6. =(
)
7. 50+52+53+54+51=(
8. 381+378+382+383+379
)
9. 1000―90―80―70―60―50―40―30―20―10
知识点讲解 3:裂相相消法
每一项都是 的分数,能拆成 - ,而且拆开后可以使前后一些分数互相抵消,达到简化运算的目的。
形如 的分数可以拆成 ×( - )。
形如 的分数可以拆成 。
例 1.
例 2.
例 3.
我爱展示
581025-393701.
2.
3.
581025-577854.
导学二 : 数论
知识点讲解 1
1、分数的意义:把单位“1”平均分成若干份,表示这样的一份或几分的数叫作分数。表示其中一份的数是这个分数的分数单位。
2、百分数的定义:像2%,5%,120%…这样的分数叫百分数,也叫百分比或百分率。表示一个数是另一个数的百分之几。
3、分数和百分数的区别: 分数既可以表示一个数,也可以表示两个数的比;而百分数只表示一个数占另一个数的百分比,不能用来表示具体数。所以分数可以有单位,百分数不能有单位。
4、几组重要的概念:
倍数和因数:倍数和因数是相互依存的。如:4×5=20,就可以说20是4和5的倍数,4和5是20的因数。
最大公因数、最小公倍数:几个数公有的因数,叫做这几个数的公因数;其中最大的一个,叫做这几个数的最大公因数。几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
奇数和偶数:能被2整除的数叫偶数(0也是偶数);不能被2整除的数叫奇数。
质数和合数:只有1和它本身两个因数的数是质数;有3个或3个以上因数的数叫合数。 0和1既不是质数也不是合数。
5、 2、3、5倍数的特征。
(1)2的倍数的特征:个位是0、2、4、6、8 的数是2的倍数;
(2)5的倍数的特征:个位上是0或者5的数是5的倍数;
(3)3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
(4)同时是2、5、3的倍数的特征:一个数各个数位上的数字的和是3的倍数,且个位上是0,这个数一定同时是2、5、3 的倍数。
例 1. (广州某外国语学校面试真题九)判断:由于0.5×6=3,所以6是3的因数。 ( ) 例 2. (广州某外国语学校面试真题九)同时被2,3,5整除的数有哪些特点?
例 3. (2014广州某外国语学校面试真题六)20到50有哪些质数?
例 4. (广州某外国语学校面试真题六)一个数四舍五入后为十万,这个数最小是几?
例 5. 甲、乙两桶油同样重,把甲桶的倒入乙桶,这时乙桶油的质量是甲桶油的( )倍。
774700-85725例 6. (填小数)
例 7. 将6克糖完全溶解在54克水中,糖占糖水的( )%。
例 8. 一台电视机按定价九折出售,可赚120元;按定价八五折出售,亏120元。问定价是多少钱?
我爱展示
(广州某外国语学校面试真题六)能被9整除的数有什么特点?
(广州某外国语学校面试真题七)1是什么数?
(广州某外国语学校面试真题十一)一个数由4个1,2个十分之一和6个百分之一组成,这个数是多少?
(广州某外国语学校面试真题五)什么样的分数可以化成有限小数?
(广州某外国语学校面试真题五)一个数最大的约数是17,问这个数是多少?
试验一批种子的发芽率,第一次取50粒,有45粒发芽,发芽率是( )%;第二次取30粒,全部发芽,发芽率是
( )%。
一杯浓度为100%纯牛奶,喝去20%,加满水搅匀,再喝去50%,杯中牛奶的浓度( )
导学三 : 计数原理
知识点讲解 容斥原理、加法原理、乘法原理
例 1. 1-100的自然数中,3的倍数和5的倍数的个数共有多少个?
例 2. 2、把5支铅笔分给甲、乙、丙三个小朋友,每个小朋友每次都有分得铅笔,有多少种不同的分法?
例 3. 某人到食堂去买饭菜,食堂里有4种荤菜,3种蔬菜,2种汤。他要各买一样,共有多少种不同的买法?
我爱展示
老师出了两道数学题,在40人中,做对第一题的有31人,做对第二题的有28人,每人至少做对一道,两道题都做对的 有几人?
用数字0、1、2、3、4、5可以组成多少个三位数(各位上的数字允许重复)?
如下图,A,B,C,D,E五个区域分别用红、黄、蓝、白、黑五种颜色中的某一种染色,要使相邻的区域染不同的颜 色,共有多少种不同的染色方法?
2532380266065
限时考场模拟 : 10 分钟完成
1. 19998+39996+49995+69996
581025-393702.
一项工程,甲独做8天完成,乙独做10天完成。两人合作4天,甲完成了这项工程的( )%,乙完成了这项工程的( )。
在a÷b=5……3中,把a、b同时扩大3倍,商是( ),余数是( )。
课后作业
1. 如果把甲班人数的调到乙班,两班人数正好相等。原来乙班人数是甲班的( )。
7747002774952. A=2 ×3×5×7,B=2×3×7,A、B的最大公因数是( ),最小公倍数是( )
3. 甲数、乙数都不为0,甲数× =乙数×60%,甲:乙=( : )。4. 1998×25=( )
5. 12.5×25×0.32
6.
2532380189865
1、学完这节课的内容后,对于以后碰到的复杂计算题,先分析数据特征,寻找是否有规律,再计算。
2、充分掌握裂项相消法,课后多找一些这类型的题目来训练。
3、理解数论的概念,总结考题的方向。
课首小测
1.889
2.1000
3.
4.14
5.5
导学一
知识点讲解 1:整数凑整
例题
=
1.1
解析:=
2.4000
3.608
4.3333
=100-99
=1
我爱展示
1.600
2.55
3.346
知识点讲解 2:稍复杂数的连加减
例题
1.11106
2.81
3.1110
我爱展示
1.111105
2.11100
3.5890
4.1400
5.649
6.1110
7.260
8.1903
9.550
知识点讲解 3:裂相相消法
例题
1.
解析:=
=
=
= 2.
解析:=
=
=
= 3.
解析:=
=
=
=
我爱展示
1.
2.
3.
4.
导学二
知识点讲解 1 例题
1.×
尾数是0,且数字之和是3的倍数。
3.23,29,31,37,41,43,47。共7个
4.95000
5.2
6.24;15;0.75
7.10%
8.(120+120)÷(90%-85%)=4800(元)
我爱展示
1.数字之和是9的倍数。
是自然数和奇数。
3.4.26
4.最简分数,而且分母只能分解2或5的质因数的分数能化成有限小数。
5.17
6.90%;100%
7.80%
导学三
知识点讲解 容斥原理、加法原理、乘法原理
例题
1.47
解析: 1-100的自然数中,3的倍数有33个,5的倍数有20个,既是3又是5的倍数有6个,所以1-100的自然数中3的倍数和5 的倍数有:33+20-7=47个
7099302000252.6种
解析:
3.4×3×2=24(种)
我爱展示
1.19人
解析: 31+28-40=19人2.5×6×6=180(个)
3.5×4×3×3×2=360(种)
限时考场模拟
1.179985
2.
3.50;
4.5;9
497205315595课后作业
1.
2.B;A(或者42;840)
3.1:1
=
=
4.49950
5.100
6.
解析:=
学生姓名
年级
学科
授课教师
日期
时段
核心内容
巧算与数论
课型
一对一
教学目标
1、让学生掌握用整数的凑整简便思想来巧算复杂的计算题;
2、理解裂相相消法,学会分析题目中数据特征,借助有关运算性质,达到简便运算;
3、理解分数、百分数、倍数的概念,掌握其解题技巧。
重、难点
掌握复杂计算题的解题技巧。
2532380114935
课首沟通
了解学生的学习进度和困难点。
回顾上次课所学内容。
368300321310知识导图
课首小测
1. (10000-1000-100-10)÷10
2. 198+297+396+495
581025-31753.
581025-762004.
581025-577855.
2532380133350
导学一 : 巧算
知识点讲解 1:整数凑整
例 1. (西关外国语面谈考试 )
例 2. (广州某外国语面试数学卷三)125×32=( ) 例 3. 487+(213-92)
例 4. 3333+3333-3333×3333÷3333
我爱展示
1. (广州某外国语面试数学卷三)25×24=( )
2. (广州某外国语面试数学卷四)25+32-2=( )
3. 432―(154―68)=( )
知识点讲解 2:稍复杂数的连加减
例 1. 9+99+999+9999
例 2. 1-2-3+4+5-6……-78-79+80+81
例 3.
我爱展示
1. 99999+9999+999+99+9=( )
2. 9+98+996+9997=(
3. 1999+2998+396+497=(
)
)
4. 487+321+113+479=(
5. 723-251+177=(
)
)
6. =(
)
7. 50+52+53+54+51=(
8. 381+378+382+383+379
)
9. 1000―90―80―70―60―50―40―30―20―10
知识点讲解 3:裂相相消法
每一项都是 的分数,能拆成 - ,而且拆开后可以使前后一些分数互相抵消,达到简化运算的目的。
形如 的分数可以拆成 ×( - )。
形如 的分数可以拆成 。
例 1.
例 2.
例 3.
我爱展示
581025-393701.
2.
3.
581025-577854.
导学二 : 数论
知识点讲解 1
1、分数的意义:把单位“1”平均分成若干份,表示这样的一份或几分的数叫作分数。表示其中一份的数是这个分数的分数单位。
2、百分数的定义:像2%,5%,120%…这样的分数叫百分数,也叫百分比或百分率。表示一个数是另一个数的百分之几。
3、分数和百分数的区别: 分数既可以表示一个数,也可以表示两个数的比;而百分数只表示一个数占另一个数的百分比,不能用来表示具体数。所以分数可以有单位,百分数不能有单位。
4、几组重要的概念:
倍数和因数:倍数和因数是相互依存的。如:4×5=20,就可以说20是4和5的倍数,4和5是20的因数。
最大公因数、最小公倍数:几个数公有的因数,叫做这几个数的公因数;其中最大的一个,叫做这几个数的最大公因数。几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
奇数和偶数:能被2整除的数叫偶数(0也是偶数);不能被2整除的数叫奇数。
质数和合数:只有1和它本身两个因数的数是质数;有3个或3个以上因数的数叫合数。 0和1既不是质数也不是合数。
5、 2、3、5倍数的特征。
(1)2的倍数的特征:个位是0、2、4、6、8 的数是2的倍数;
(2)5的倍数的特征:个位上是0或者5的数是5的倍数;
(3)3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
(4)同时是2、5、3的倍数的特征:一个数各个数位上的数字的和是3的倍数,且个位上是0,这个数一定同时是2、5、3 的倍数。
例 1. (广州某外国语学校面试真题九)判断:由于0.5×6=3,所以6是3的因数。 ( ) 例 2. (广州某外国语学校面试真题九)同时被2,3,5整除的数有哪些特点?
例 3. (2014广州某外国语学校面试真题六)20到50有哪些质数?
例 4. (广州某外国语学校面试真题六)一个数四舍五入后为十万,这个数最小是几?
例 5. 甲、乙两桶油同样重,把甲桶的倒入乙桶,这时乙桶油的质量是甲桶油的( )倍。
774700-85725例 6. (填小数)
例 7. 将6克糖完全溶解在54克水中,糖占糖水的( )%。
例 8. 一台电视机按定价九折出售,可赚120元;按定价八五折出售,亏120元。问定价是多少钱?
我爱展示
(广州某外国语学校面试真题六)能被9整除的数有什么特点?
(广州某外国语学校面试真题七)1是什么数?
(广州某外国语学校面试真题十一)一个数由4个1,2个十分之一和6个百分之一组成,这个数是多少?
(广州某外国语学校面试真题五)什么样的分数可以化成有限小数?
(广州某外国语学校面试真题五)一个数最大的约数是17,问这个数是多少?
试验一批种子的发芽率,第一次取50粒,有45粒发芽,发芽率是( )%;第二次取30粒,全部发芽,发芽率是
( )%。
一杯浓度为100%纯牛奶,喝去20%,加满水搅匀,再喝去50%,杯中牛奶的浓度( )
导学三 : 计数原理
知识点讲解 容斥原理、加法原理、乘法原理
例 1. 1-100的自然数中,3的倍数和5的倍数的个数共有多少个?
例 2. 2、把5支铅笔分给甲、乙、丙三个小朋友,每个小朋友每次都有分得铅笔,有多少种不同的分法?
例 3. 某人到食堂去买饭菜,食堂里有4种荤菜,3种蔬菜,2种汤。他要各买一样,共有多少种不同的买法?
我爱展示
老师出了两道数学题,在40人中,做对第一题的有31人,做对第二题的有28人,每人至少做对一道,两道题都做对的 有几人?
用数字0、1、2、3、4、5可以组成多少个三位数(各位上的数字允许重复)?
如下图,A,B,C,D,E五个区域分别用红、黄、蓝、白、黑五种颜色中的某一种染色,要使相邻的区域染不同的颜 色,共有多少种不同的染色方法?
2532380266065
限时考场模拟 : 10 分钟完成
1. 19998+39996+49995+69996
581025-393702.
一项工程,甲独做8天完成,乙独做10天完成。两人合作4天,甲完成了这项工程的( )%,乙完成了这项工程的( )。
在a÷b=5……3中,把a、b同时扩大3倍,商是( ),余数是( )。
课后作业
1. 如果把甲班人数的调到乙班,两班人数正好相等。原来乙班人数是甲班的( )。
7747002774952. A=2 ×3×5×7,B=2×3×7,A、B的最大公因数是( ),最小公倍数是( )
3. 甲数、乙数都不为0,甲数× =乙数×60%,甲:乙=( : )。4. 1998×25=( )
5. 12.5×25×0.32
6.
2532380189865
1、学完这节课的内容后,对于以后碰到的复杂计算题,先分析数据特征,寻找是否有规律,再计算。
2、充分掌握裂项相消法,课后多找一些这类型的题目来训练。
3、理解数论的概念,总结考题的方向。
课首小测
1.889
2.1000
3.
4.14
5.5
导学一
知识点讲解 1:整数凑整
例题
=
1.1
解析:=
2.4000
3.608
4.3333
=100-99
=1
我爱展示
1.600
2.55
3.346
知识点讲解 2:稍复杂数的连加减
例题
1.11106
2.81
3.1110
我爱展示
1.111105
2.11100
3.5890
4.1400
5.649
6.1110
7.260
8.1903
9.550
知识点讲解 3:裂相相消法
例题
1.
解析:=
=
=
= 2.
解析:=
=
=
= 3.
解析:=
=
=
=
我爱展示
1.
2.
3.
4.
导学二
知识点讲解 1 例题
1.×
尾数是0,且数字之和是3的倍数。
3.23,29,31,37,41,43,47。共7个
4.95000
5.2
6.24;15;0.75
7.10%
8.(120+120)÷(90%-85%)=4800(元)
我爱展示
1.数字之和是9的倍数。
是自然数和奇数。
3.4.26
4.最简分数,而且分母只能分解2或5的质因数的分数能化成有限小数。
5.17
6.90%;100%
7.80%
导学三
知识点讲解 容斥原理、加法原理、乘法原理
例题
1.47
解析: 1-100的自然数中,3的倍数有33个,5的倍数有20个,既是3又是5的倍数有6个,所以1-100的自然数中3的倍数和5 的倍数有:33+20-7=47个
7099302000252.6种
解析:
3.4×3×2=24(种)
我爱展示
1.19人
解析: 31+28-40=19人2.5×6×6=180(个)
3.5×4×3×3×2=360(种)
限时考场模拟
1.179985
2.
3.50;
4.5;9
497205315595课后作业
1.
2.B;A(或者42;840)
3.1:1
=
=
4.49950
5.100
6.
解析:=
